Матричный алгоритм шифрования

Автор: Саломатин Кирилл Сергеевич

Опубликовано: 24.04.2012
Исправлено: 10.12.2016
Версия текста: 1.1

Введение Постановка задачи Современные алгоритмы Новый класс алгоритмов Шифрование Дешифрование Особенности алгоритма Вывод Список литературы

Введение

Приносим читателям свои извинения за публикацию этой статьи. Статья очень плоха, см. подробнее в обсуждении на форуме. Торопились сдать номер, понадеялись на автора, недоглядели. Ещё раз извините.

Система определения движущихся объектов является довольно востребованной, т.к. помогает облегчить задачу многим службам, например, авиадиспетчерам. Но, как и в любой системе, в системе определения движущихся объектов необходимо производить шифрование информации на пути от датчика до системы анализа полученных данных.

Постановка задачи

Необходимо разработать алгоритм шифрования данных для системы определения движущихся объектов.

Современные алгоритмы

На данный момент самыми распространенными классами алгоритмов являются симметричные алгоритмы и асимметричные, т.е. системы с открытым ключом.

На рис.1-4 представлена схема работы симметричного алгоритма шифрования AES, который является государственным стандартом шифрования США с 2001года:

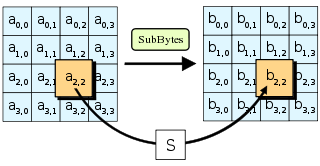
Рис.1 «Шаг 1»

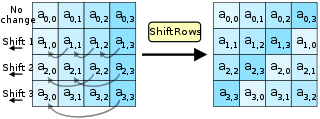
Рис.2 «Шаг 2»

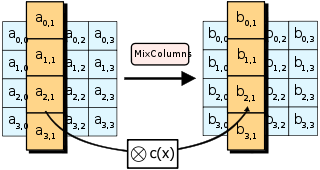
Рис.3 «Шаг 3»

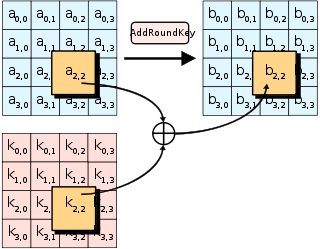
Рис.4 «Шаг 4»

Еще одним из распространенных алгоритмов является асимметричный алгоритм, или система с открытым ключом.

Идея криптографии с открытым ключом очень тесно связана с идеей односторонних функций, то есть таких функций f(x), что по известному x довольно просто найти значение f(x), тогда как определить x из f(x) невозможно. Поэтому криптография с открытым ключом использует односторонние функции с лазейкой. Лазейка — это некий секрет, который помогает расшифровать текст. То есть существует такой y, что зная f(x) и y, можно вычислить x. К примеру, если разобрать часы на множество составных частей, то очень сложно собрать вновь работающие часы. Но если есть инструкция по сборке (лазейка), то можно легко решить эту проблему.

Новый класс алгоритмов

В данной работе представлен новый класс алгоритмов. В отличие от описанных алгоритмов, в данном применяется новый подход к кодированию информации.

Шифрование

1. Удалить повторяющиеся символы и сохранить количество повторений и номера позиций этих символов в тексте (эти данные составляют ключи.)
2. Вычислить номер символа в таблице ASCII.
3. ASCII представляет собой кодировку для представления десятичных цифр, латинского и национального алфавитов, знаков препинания и управляющих символов.
4. Построить 3 матрицы, где одна матрица – номера символов текста, вторая состоит из количества повторений этих символов, а третья состоит из номеров позиций символов в тексте, где каждая срока соответствует одному символу.
5. Перемножить первые 2 матрицы. После этого действия должна получиться квадратная матрица, т.к. при дешифровании необходимо будет найти обратную матрицу, которую необходимо будет умножить на матрицу повторений.
6. Перемешать текст по правилу: первая позиция – номер позиции элемента, вторая позиция – символ из п.4, а на 3-м – количество повторений.
7. Произвести гаммирование полученного текста.

Гаммирование – преобразование исходного (открытого) текста, при котором символы исходного текста складываются (по модулю, равному мощности алфавита) с символами псевдослучайной последовательности, вырабатываемой по определенному правилу. Гамма в криптографии – псевдослучайная числовая последовательность, вырабатываемая по определенному алгоритму и используемая для зашифровывания открытых данных и расшифровывания зашифрованных данных. Наложение гаммы происходит по формуле αi=βi+γi(mod n), где βi – исходный текст, γi – гамма, n – основание используемого алфавита, αi – результат.

Дешифрование

1. Произвести гаммирование. Особенность гаммирования в том, что если произвести над шифротекстом повторное гаммирование, то получится исходный текст.
2. Полученный текст необходимо разбить на 3 части по правилу, используемому при шифровании. Получится 3 матрицы – шифротекст, количество повторений и номера позиций.
3. Необходимо найти обратную матрицу шифротекста и перемножить её с матрицей повторений.
4. Теперь необходимо полученную матрицу перевести в символы и сопоставить с матрицей повторений и матрицей позиций. И в итоге получится исходный текст.

Особенности алгоритма

1. Динамическое формирование ключей. Ключи формируются только для конкретного момента и данных и для других данных они не подходит.
2. Изменение одного символа в исходном тексте приводит к полному изменению зашифрованного текста.
3. Данный алгоритм имеет составной ключ, состоящий из двух частей и для дешифрации необходимо наличие всех частей.
4. Изменение одного символа в исходном тексте приводит к полному изменению зашифрованного текста.
5. Исходный и финальный тексты не совместимы ни по чтению, ни по длине. Данное свойство не позволяет напрямую, простыми методами подобрать исходный текст.
6. Отсутствие циклов в работе алгоритма.
7. Использование данного алгоритма не позволяет подобрать ключи, отличные от реальных, такие, что позволяют получить исходный текст.

Вывод

Сфера деятельности современных алгоритмов четко разделена – асимметричные алгоритмы применяются в основном в сетевых протоколах, а симметричные применяется во всем остальном.

Представленный же здесь алгоритм, в связи со своей динамичностью, универсален и может применяться не только в системе обнаружения движущихся объектов, но и в любой другой.

Источник

Матричный метод шифрования

выберим матрицу А(4,4)
открытый объект: Меня зовут Иван

закрытый объект: м увезтано няи

Помогите пожалуйста написать код.
Вот что у меня получилось:

Метод шифрования
всем привет. подскажите, каким методом шифрования получено значение.

Метод шифрования RSA
помогите найти ошибку, код не правильно работает 6

Решение

спасибо, но тут создается матрица автоматически относительно длинны строки, я правильно понял? Например если длина строки равно 255, то размер матрицы будет равно 15 приблизительно.
А можно, так, чтобы например матрица была размером 5х5 и использовалась до последнего символа текста.
Примерно так:

Решение

Матричный метод решения системы
Матричным методом решить системы.Что не так?? Не могу понять как правельно сделать. k=4; U=;.

Матричный метод решения СЛАУ
Доброго времени суток. Нужно решить систему линейных уравнений с 4-мя переменными матричным.

Матричный метод решения СЛАУ
Здравствуйте уважаемые програмисты, не могу осилить данный метод, и в нете инфы очень мало, может у.

Как можно найти алгебраическое дополнение в матрице (матричный метод, СЛАУ)
Здравствуйте! Подскажите,пожалуйста, как можно найти алгебраическое дополнение в матрице(матричный.

Источник

кто может объяснить принцип шифрования ключей к играм и способы их вскрытия

Безопасность зашифрованных данных обеспечивается не только сильными алгоритмами шифрования. Несоблюдение принципов использования ключей шифрования может поставить под угрозу защищенность информации даже при том, что в системе будут реализованы самые криптостойкие алгоритмы.

Предположим, есть два пользователя (назовем их I и J), решивших обмениваться зашифрованными сообщениями через Интернет. Посмотрим, как можно это сделать, на примере комплексного метода шифрования.
Комплексный метод

Этот метод применения алгоритмов симметричного и асимметричного шифрования устраняет ряд недостатков, свойственных каждому из них при раздельном применении. Итак, чтобы обменяться зашифрованными сообщениями через Интернет, пользователям I и J необходимо предварительно сделать следующее.

1. Выбрать алгоритмы шифрования и их параметры. Вспомним (см. статью «Современные алгоритмы шифрования», «BYTE/Россия» No 8’2003), что каждый алгоритм имеет множество параметров, которые должны быть идентичны, — иначе даже при наличии правильного ключа шифрования будет невозможно расшифровать информацию. Например, для алгоритма ГОСТ 28147-89 должны быть согласованы таблицы замен, используемый режим алгоритма и принципы формирования синхропосылок.

2. Сгенерировать свои ключи асимметричного шифрования. Пользователь I генерирует пару ключей KsI (secret — секретный) и KpI (publIc — открытый) , пользователь J создает пару KsJ и KpJ.

3. Обменяться открытыми ключами или сделать их доступными друг другу. Предположим, что открытые ключи KpI и KpJ пользователи пересылают друг другу по электронной почте.

Не будем рассматривать здесь проблему перехвата открытых ключей при передаче и их подмены злоумышленником — это тема отдельного разговора. Предположим, ключи успешно переданы и получены, после чего можно отправлять зашифрованное сообщение. Это и делает пользователь J, отправляя пользователю I сообщение M.

Процесс обмена иллюстрирует рис. 1. Перед передачей сообщения пользователь J создает случайный ключ симметричного шифрования (назовем его Ksimm). Пользователь J асимметрично зашифровывает ключ Ksimm на открытом ключе пользователя I KpI и отправляет зашифрованный ключ пользователю I. Затем пользователь J зашифровывает ключом Ksimm сообщение M, и полученный шифртекст C отсылается пользователю I. Пользователь I получает зашифрованный ключ Ksimm и асимметрично расшифровывает его своим секретным ключом KsI. С помощью полученного ключа Ksimm пользователь I расшифровывает сообщение M.
Рис. 1. Комплексный метод шифрования.

Как было отмечено выше, недостатки алгоритмов симметричного и асимметричного шифрования при их совместном использовании частично компенсируются. В частности, скрытое распространение ключей симметричного шифрования достигается за счет того, что симметричный ключ Ksimm, на котором шифруется собственно информация, передается по открытым каналам связи в зашифрованном виде — для его зашифрования используется асимметричный алгоритм, не имеющий проблем с секретностью. Проблемы малой скорости асимметричного шифрования в данном случае практически не возникает, поскольку асимметричным алгоритмом шифруется только короткий ключ Ksimm, а все данные шифруются быстрым симметричным алгоритмом. Результат — быстрое шифрование в сочетании с удобным обменом ключами.
Ключевые схемы

Манипуляции с зашифрованием ключа Ksimm и его передачей вместе с сообщением являют собой пример ключевой схемы (так называются схемы использования ключей шифрования) . В общем случае для разработки какой-либо системы, позволяющей шифровать файлы или сообщения, недостаточно просто реализовать алгоритм шифрования. Необходимо также продумать принципы генерации, передачи, хранения и использования ключей шифрования: так как недостаточная защита ключей на любом из этих этапов или неправильное их применение поставит под угрозу всю зашифрованную информацию. Ведь любая «слабость» этапов шифрования даст возможность злоумышленнику атаковать систему защиты с тем, чтобы полу

Источник

Шифрование и математика

Разделы: Математика

Основная цель – на популярном, практически игровом уровне познакомить учащихся с применением математики для решения задач кодирования и декодирования информации.

I. Постановка задачи.

II. Секретная переписка подпольщиков.

III. Роль математики в расшифровке. Способ шифровки — кодирование, декодирование.

IV. Матричный способ шифровки.

I. Зачем нужно шифровать те или иные тексты, от содержащих государственные тайны — до записок знакомой девочке или мальчику?

Веками создавались самые различные системы тайнописи, которыми владели только «посвященные», умевшие и зашифровать текст, и расшифровать его. Конечно, для «непосвященных» разгадать шифр всегда было очень важно. Поэтому веками разрабатывались как способы расшифровки чужих шифров, так и способы создания своих шифров, которые не поддавались бы расшифровке. Проблема расшифровки связана не только с секретами, которые следует скрыть от посторонних, но и с серьезными проблемами гуманитарных наук – например, истории и археологии, прежде всего с «воскрешением» так называемых мертвых языков. Так, древняя цивилизация в Египте оставалась за семью печатями до тех пор, пока в XIX веке французский филолог Шампольон не смог расшифровать иероглифы, которые древним египтянам были хорошо понятны. А в XX в. Наш соотечественник, ученый, историк, лингвист и этнограф Ю.В.Кнозоров расшифровал письменность древнего народа майя, жившего много веков назад на территории нынешней Мексики.

II. Послушайте рассказ о секретной переписке подпольщиков. [2]

Революционер – подпольщик вынужден вести свои записи и переписку с товарищами таким образом, чтобы никто из посторонних не мог понять написанного. Для этого пользуются особым способом письма, называемым «тайнописью». Придуманы разные системы тайнописи; к их услугам прибегают не одни подпольщики, но также дипломаты и военные для сохранения государственных тайн. Сегодня я хочу рассказать об одном из таких способов ведения секретной переписки, а именно: о так называемом способе «решетки». Он принадлежит к числу сравнительно простых и тесно связан с арифметикой.

Желающие вести тайную переписку по этому способу запасаются каждый «решеткой», т.е. бумажным квадратиком с прорезанными окошечками. . (Раздается ученикам «решетки»).

Пусть требуется послать товарищу такую записку:

Собрание делегатов отмените.

Полиция кем-то предупреждена. Антон.

Наложив решетку на листок бумаги, подпольщик пишет сообщение букву за буквой в окошечках решетки. Так как окошек 16, то сначала помещается только часть записки:

Сняв решетку, вы увидите запись, представленную на рисунке 2,

Здесь, разумеется, ничего засекреченного пока нет: каждый легко поймет, в чем дело. Но это только начало; записка в таком виде не останется. Подпольщик поворачивает решетку «по часовой стрелке» на четверть оборота, т.е. располагает ее на том же листке так, что цифра 2, бывшая раньше сбоку, теперь оказывается вверху. При новом положении решетки все раньше написанные буквы заслонены, а в окошечках появляется чистая бумага. В них пишут следующие 16 букв секретного сообщения.

Такую запись не поймет не только посторонний человек, но и сам писавший, если позабудет текст своего сообщения.

Чтобы писать дальше, надо вновь повернуть решетку на четверть оборота по часовой стрелке. Она закроет все написанное и откроет новые 16 свободных клеток.

Наконец делается последний поворот решетки цифрой «4» вверх, и в открывшиеся 16 чистых квадратиков вписывают окончание записки. Так как остаются три неиспользованные клетки, их заполняют буквами а, б, в – просто для того, чтобы в записке не оказалось пробелов.

Письмо имеет вид, представленный на рисунке 3.

Попробуйте в нем что-нибудь разобрать! Пусть записка попадет в руки полиции, пусть полицейские сколько угодно подозревают, что в ней скрыто важное сообщение, — догадаться о содержании записки они не смогут. Никто из посторонних не разберет в ней ни единого слова. Прочесть ее в состоянии только адресат, имеющий в руках точно такую же решетку, как и та, которой пользовался отправитель.

Как же прочтет адресат это секретное письмо? Он наложит свою решетку на текст, обратив ее цифрой «1 вверх, и выпишет те буквы, которые появятся в окошечках. Это будут первые 16 букв сообщения. Затем повернет решетку — и перед ним предстанут следующие 16 букв. После четвертого поворота вся секретная записка будет прочитана.

III. Огромную роль в проблеме расшифровки текстов играет, как ни странным это может показаться, математика, прежде всего теория вероятностей и математическая статистика. [1]

Сегодня мы с вами познакомимся с одним очень простым способом шифрования. Чтобы воспользоваться им для шифровки и расшифровки ( кодирования и декодирования), достаточно знать лишь простейшую арифметику, порядок букв в алфавите и помнить всего… четыре числа. А расшифровать ваш текст непосвященному человеку будет абсолютно не под силу.

Для кодирования текста на русском языке занумеруем все буквы по месту их расположения в алфавите – от 1 до 33, добавив 34-ю пробел.

Возьмем какое-нибудь простое предложение, например, «шёл снег», и каждую букву заменим соответствующей цифрой. Получим последовательность: 26,7, 13, 34, 19, 15, 6, 4.

IV. Построим из этой последовательности две таблички 2х2:

Такие таблички из четырех чисел называются матрицей.

Зашифруем эту последовательность с помощью еще одной матрицы — кодирующей – по следующему правилу:

Такой способ шифрования и называют матричным. Ваш адресат получит текст: 91, 116, 52, 75, 56, 42, 31, 23.

А как же он его расшифрует? Оказывается, и это нетрудно: он должен взять декодирующую матрицу

и проделать с полученным текстом то же самое, что делали мы с исходным текстом.

После замены матриц на последовательность 26,7, 13, 34, 19, 15, 6, 4, а затем — чисел на буквы дешифровальщик получит исходный текст «шёл снег».

Ясно, что никто посторонний, не знающий ни кодирующей, ни декодирующей матрицы, получить этот текст не сможет.

Однако матричный способ шифрования не смог бы существовать, если бы в качестве кодирующей можно было брать только матрицу

На самом деле таких матриц бесконечно много, придумывать их очень легко. И вообще вы можете менять свою систему «тайнописи» каждый день. Для этого нужно знать очень немного – уметь любые две матрицы «перемножать», т.е. по определенному правилу составлять из них третью.

– правило умножения матриц. .

А теперь, по правилу умножения:

1. Перемножьте матрицы:

2. Зашифруйте текст «Вы мне дороги».

На следующем занятии мы поговорим с вами об алгебре матриц, а также будем друг-другу писать письма, а для этого необходимо будет придумать свою кодирующую матрицу. Подумайте о том, какая у вас будет эта матрица?

1. Дорофеев Г.В. и др. Курс по выбору для 9 класса «Избранные вопросы математики»//Математика в школе, 2003, № 10, с. 2-36.

2. Я.И.Перельман «Живая математика».- М.: Издательство «Просвещение», 1995.

Источник