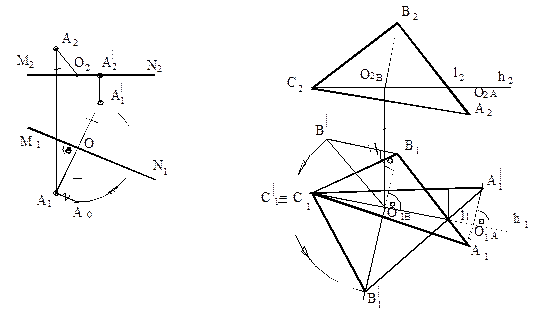Сущность способа вращения заключается

Содержание

Способ вращения
Метод вращения
Метод вращения вокруг оси
Способ вращения вокруг проецирующей прямой
Способ вращения вокруг линии уровня
Научная электронная библиотека
5.5. Способ вращения. Вращение вокруг проецирующей прямой

Способ вращения

Вращение вокруг оси, перпендикулярной плоскости проекции, является частным случаем параллельного перемещения. Отличие от параллельного перемещения состоит лишь в том, что за траекторию перемещения точки берется не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между точкой и осью вращения.

Способ вращения вокруг оси, перпендикулярной плоскости проекции, применим для перемещения отрезка прямой общего положения в частное.

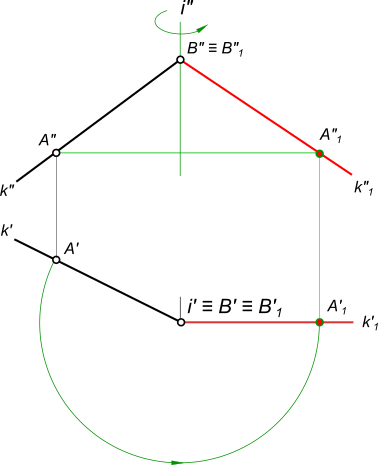
Перевод прямой общего положения k в положение перпендикулярное горизонтальной плоскости проекции H.

Здесь необходимо дважды применить способ вращения вокруг осей, перпендикулярных к плоскостям проекции. Первым вращением отрезок переводится в положение, параллельное плоскости проекции V, и лишь после этого вращением вокруг оси перпендикулярной плоскости проекции V, перемещают отрезок в положение, перпендикулярное плоскости H .

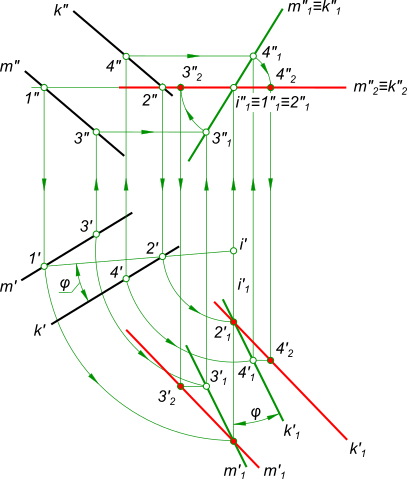
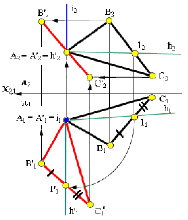
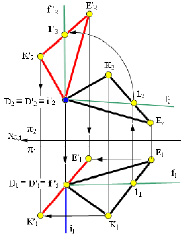
Перевод плоскости общего положения в частное фронтально проецирующее положение.

Прямую, принадлежащую плоскости произвольно расположенной в пространстве, используя способ вращения переводим в положение перпендикулярное плоскости V. Используем для этого горизонталь плоскости, заданную точками 1 и 2 на рисунке.

Используем способ вращения напоследок, для придания плоскости положения параллельного плоскости проекции H, то есть положения плоскости уровня. Используем для этого ось вращения i₁.

Источник

Метод вращения

Сущность метода вращения заключается в том, что плоскости проекций остаются неподвижными, а меняется положение объекта проецирования путем вращения вокруг неподвижной оси до удобного положения для проведения необходимых построений.

Если ось вращения не задана, ее располагают перпендикулярно к одной из плоскостей проекций, так как упрощаются все построения при решении задач.

Действительно, если ось вращения перпендикулярна к какой – либо плоскости проекций, то плоскость , в которой вращается точка, параллельна этой плоскости проекций. Траектория движения точки на эту плоскость проекций проецируется без искажения, а на вторую плоскость проекций проецируется в виде отрезка прямой линии.

Вращение вокруг оси, перпендикулярной плоскости проекций

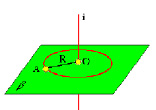
Рассмотрим этот метод на примере (рисунок 79) поворота точки А вокруг оси i, перпендикулярной плоскости П₁, на некоторый угол. Траектория перемещения точки – окружность, плоскость которой перпендикулярна оси i и параллельна плоскости П₁. Поэтому на плоскость П₁ проецируется без искажения. Фронтальная проекция этой траектории будет прямая, параллельная оси Х. Точка О является центром вращения точки А, а отрезок А₁О₁=А₁ / О₁ – радиус вращения.

Рисунок 79 Рисунок 80

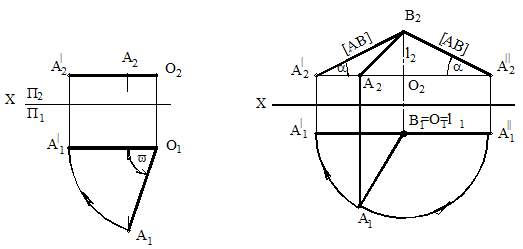
Пример. Определить длину отрезка АВ и угол наклона его к горизонтальной плоскости проекций П₁ (рисунок 80).

Ось вращения i проходит через точку В и перпендикулярна П₁. Вращая отрезок АВ вокруг оси i, в положение параллельное фронтальной плоскости проекций П₂, позволяет спроецировать отрезок на эту плоскость без искажения. При вращении точка А перемещается по дуге в плоскости, параллельной плоскости П₁ до положения пока А₁ / В₁ станет параллельно оси Х. При этом фронтальная проекция А₂ перемещается по прямой А₂А₂ / параллельной оси Х. Отрезок [АВ]=[А₂ / В₂].

Вращение вокруг линии уровня

Форму плоской фигуры, занимающей общее положение относительно плоскостей проекций, можно определить поворотом вокруг ее горизонтали (или фронтали) в положение, параллельное соответствующей плоскости проекций. На рисунке 81 показано вращение точки А вокруг горизонтальной прямой MN до тех пор, пока точка А не окажется в плоскости, параллельной плоскости проекций П₁ и определяемой этой точкой и осью вращения.

При вращении вокруг горизонтальной прямой MN точка перемещается по дуге радиуса ОA₀, лежащей в плоскости Р, перпендикулярной к оси вращения. Когда точка A займет нужное положение A₁, горизонтальная проекция радиуса вращения (ОА₁ / ) будет равна его истинной величине, которая может быть определена способом прямоугольного треугольника.

Рисунок 81 Рисунок 82

Пример. Определить истинную величину треугольника АВС (рисунок 82).

Возьмем в качестве оси вращения горизонталь C1(h₁). Так как ось вращения параллельна плоскости П₁, траектории перемещения вершин А и В будут проецироваться на эту плоскость в виде прямых, перпендикулярных проекции С₁1₁.Точки О_А и О_В пересечения плоскостей этих траекторий с осью С1(h₁) являются центрами вращения соответствующих вершин треугольника. Радиусы вращения точек А и В в исходном положении проецируются на плоскости П₁ и П₂ с искажением. Когда плоскость АВС в результате поворота займет горизонтальное положение, радиусы ВО_В и АО_А спроецируются на плоскость П₁ в истинную величину.

На рисунке 82 для построения проекции А₁ / В₁ / С₁ / треугольника в горизонтальном положении, достаточно любым способом найти истинную величину радиуса ВО_1В или АО_1А и отложить ее на горизонтальной проекции траектории перемещения соответствующей вершины. В примере истинная величина радиуса вращения ВО равна В / O_1В.

О_1ВВ / найдена способом прямоугольного треугольника и этим радиусом отложено расстояние от оси вращения до нового положения вершины В₁ / . Сторона А₁ / В₁ / проведена из вершины В₁ / через 1₁ до пересечения с горизонтальной проекцией плоскости вращения точки А. А₁ / В₁ / С₁ / – истинная величина треугольника АВС.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Метод вращения вокруг оси

Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линию уровня или проецирующую прямую.

Способ вращения вокруг проецирующей прямой

Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.

Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.

Читайте также: Читерский способ что это

Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.

При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C’ переместим по дуге окружности радиусом C’D’ в положение C’₁ так, чтобы выполнялось условие C’₁D’₁ || X. Для нахождения точки C»₁ из C» проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C’₁.

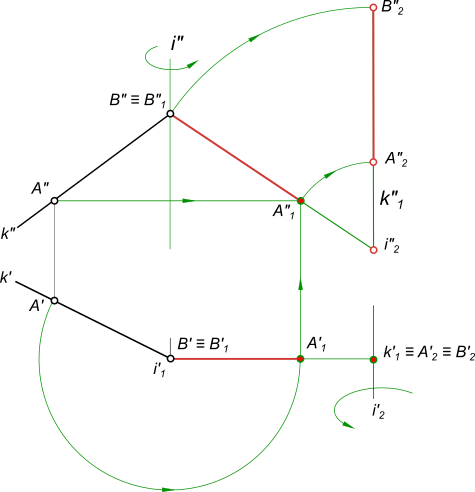
На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.

Сначала вращением вокруг оси i₁ CD перемещают в положение C₁D₁, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i₂ отрезок переводится в искомое положение C₂D₂, где он перпендикулярен горизонтальной плоскости проекции.

Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i₁ проходит через точку D, а проекция i»₂ фронтально проецирующей прямой i₂ лежит на продолжении отрезка C»₁D»₁.

Способ вращения вокруг линии уровня

Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.

Основные правила построения

Радиус вращения точки равен расстоянию между точкой и линией уровня, выполняющей роль оси. Натуральную величину радиуса определяют методом прямоугольного треугольника.
При вращении вокруг горизонтали h точка перемещается по окружности, которая проецируется на горизонтальную плоскость в отрезок прямой, перпендикулярный горизонтальной проекции горизонтали h’. На фронтальную плоскость окружность, по которой движется точка, проецируется в эллипс. Строить его нет необходимости.
При вращении вокруг фронтали f точка перемещается по окружности, которая проецируется на фронтальную плоскость в отрезок прямой, перпендикулярный фронтальной проекции фронтали f». Вместе с тем горизонтальная проекция линии перемещения представляет собой эллипс, строить который не обязательно.

Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.

Проводим фронтальную проекцию h» горизонтали h. Она пересекает прямые a» и b» в точках 1» и 2». Определяем горизонтальные проекции 1′ и 2′ и через них проводим h’.
Находим центр вращения O. Его горизонтальная проекция O’ лежит на пересечении прямой h’ с перпендикуляром, проведенным из A’ к h’.
Определяем натуральную величину радиуса вращения R = O’A’₀. Для этого строим прямоугольный треугольник O’A’A’₀, катет которого A’A’₀ равен расстоянию от A» до h».
Проводим дугу окружности радиусом R до пересечения её с прямой O’A’ в точке A’₁. Соединяем A’₁ с точками 1′ и 2′. Искомый угол ϕ построен.

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф Ф.,

5.5. Способ вращения. Вращение вокруг проецирующей прямой

Сущность этого способа заключается в том, что система плоскостей проекций П2/П1 остается неподвижной, а положение геометрических элементов изменяется путем вращения вокруг одной или двух выбранных осей до нужного положения в данной системе. В качестве оси вращения в этом случае удобнее всего выбирать проецирующие прямые или прямые уровни, тогда точка будет вращаться в плоскостях, параллельных или перпендикулярных плоскостям проекций.

При вращении используются следующие элементы вращения:

– ось вращения – прямая, вокруг которой осуществляется вращение.

– плоскость вращения – плоскость, проходящая через вращаемую точку и перпендикулярная оси вращения (плоскость окружности, которую описывает точка при вращении).

– центр вращения – точка пересечения оси вращения и плоскости вращения.

– радиус вращения – кратчайшее расстояние от вращаемой точки до центра (оси) вращения. Радиус всегда перпендикулярен оси вращения.

– угол поворота – угол между начальным и конечным положением радиуса вращения.

При вращении системы точек вокруг одной оси все точки вращаются в плоскостях, параллельных между собой, поворачиваются на один и тот же угол в одном и том же направлении, поэтому вращение является частным случаем плоскопараллельного перемещения. Точки, находящиеся на оси вращения остаются неподвижными.

Способ вращения состоит в том, что данная геометрическая фигура вращается вокруг некоторой неподвижной оси до требуемого положения относительно неподвижных плоскостей проекций. При этом каждая точка фигуры, например точка А (рис. 5.13), описывает окружность, расположенную в плоскости β, перпендикулярной оси вращения i. Центр O этой окружности является точкой пересечения оси вращения с плоскостью β. Радиус окружности равен расстоянию точки А до оси i (|R| = |AO|).

При вращении точки вокруг оси, перпендикулярной горизонтальной плоскости проекций, ее фронтальная проекция перемещается перпендикулярно линиям связи, а горизонтальная – по окружности, центром которой является горизонтальная проекция оси вращения.

Рис. 5.13. Пример вращения точки вокруг оси,
перпендикулярной плоскости

При вращении точки вокруг оси, перпендикулярной фронтальной плоскости проекций, ее горизонтальная проекция перемещается перпендикулярно линиям связи, а фронтальная – по окружности, центром которой является фронтальная проекция оси вращения (рис. 5.14).

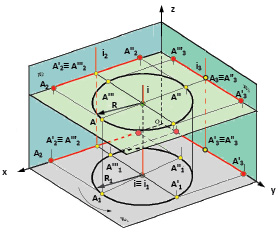
Рассмотрим вращение точки A(A1,A2,А3) вокруг горизонтально проецирующей прямой i (i1,i2,i3).

При вращении точка описывает окружность, плоскость которой β(β2) перпендикулярна оси i (i1,i2,i3). Поскольку i ⊥ П1, а β(β2) ⊥ i, β(β2) // П1 и угол поворота проецируется на П1 в натуральную величину.

Рассмотрим вращение точки A(A1,A2,А3) вокруг горизонтально проецирующей прямой i (i1,i2,i3).

Таким образом, при вращении вокруг горизонтально проецирующей прямой i(i1,i2) проекции точки A1, А’1, А»1, А»’1 перемещаются по окружности ℓ1 с центром в точке О1 и радиусом R = R1 = ОА = O1A1, фронтальные проекции A2, А’2, А»2, А»’2 перемещается по проекции фронтального следа плоскости β2 в пределах отрезка [А2,А»2].

Рассмотрим вращение точки A(A1,A2,А3) вокруг горизонтально проецирующей прямой i(i1,i2,i3).

Рис. 5.14. Пример вращения точки А вокруг
горизонтально проецирующей прямой i (i ⊥ П1)

При вращении точка описывает окружность, плоскость которой β(β2) перпендикулярна оси i(i1,i2,i3). Поскольку i ⊥ П, а β(β2) ⊥ i, β(β2) // П1 угол поворота проецируется на П1в натуральную величину.

Таким образом, при вращении вокруг горизонтально проецирующей прямой i(i1,i2) проекции точки A1, А’1, А»1, А»’1перемещаются по окружности ℓ1 с центром в точке О1 и радиусом R = R1= ОА = O1A1, фронтальные проекции A2, А’2, А»2, А»’2 перемещается по проекции фронтального следа плоскости β2 в пределах отрезка [А2, А»2].

Если точка А вращается вокруг оси i ⊥ П1, то плоскость β, в которой располагается окружность, описываемая точкой, становится горизонтальной плоскостью уровня (β || П1).

Следовательно, окружность, описываемая точкой А в пространстве, спроецируется на плоскость П1 без искажения, а на плоскость П2 – в отрезок прямой A2 А»2, совпадающей с фронтальным следом плоскости β2.

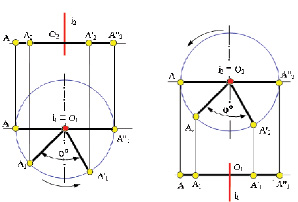
Таким образом, вращение точки A вокруг горизонтально проецирующей прямой i(i1,i2) на комплексном чертеже (рис. 5.15.а) изображено следующим образом:

1) горизонтальная проекция A1, точки А перемещается по окружности радиуса | R | = | АО | = | А1О1 |;

2) фронтальная проекция А2 точки А перемещается по прямой, перпендикулярной линиям связи (вырожденная фронтальная проекция β2 плоскости β ║П1);

3) угол поворота φ° горизонтальной проекции A1 точки А равен углу поворота точки в пространстве.

Рис. 5.15. Вращение точки А вокруг горизонтально проецирующей (а)
и фронтально проецирующей (б) прямых

Вращение точки A вокруг фронтально проецирующей прямой i(i1,i2) на комплексном чертеже (рис. 5.15.б) изображено следующим образом:

4) фронтальная A2, точки А перемещается по окружности радиуса R = | АО | = | А2О2 |;

5) горизонтальная проекция А1 точки А перемещается по прямой, перпендикулярной линиям связи (вырожденная горизонтальная проекция β1 плоскости β ║П2);

6) угол поворота φ° фронтальной проекции точки А равен углу поворота точки в пространстве.

Способом вращения тоже можно решать все основные на преобразование комплексного чертежа.

Задача 1. Преобразовать прямую общего положения в линию уровня.

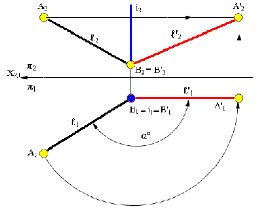
Для того чтобы прямую общего положения ℓ(ℓ1, ℓ2) преобразовать, например, во фронталь, ее необходимо вращать около оси i ⊥ П1 (рис. 5.16).

Рис. 5.16. Преобразование прямой линии общего положения
во фронтальную (фронталь) прямую

Для решения задачи необходимо:

1) выбрать две точки А(А1А2) и В(В1В2), принадлежащие прямой ℓ;

2) провести ось вращения i(i1,i2) перпендикулярно П1 через точку В(В1В2) прямой ℓ(ℓ1, ℓ2);

3) при вращении прямой ℓ вокруг оси i точка В прямой останется неподвижной, так как принадлежит оси, а точка А будет вращаться по правилам, рассмотренным выше;

4) угол поворота α° точки А и ее горизонтальной проекции А1 определяется между положением проекций А1В1 и А’1В’1.

Когда прямая ℓ займет положение параллельное П2, ее горизонтальная проекция ℓ’1 расположится перпендикулярно линиям связи.

Для определения положения проекции А’2 необходимо из А’1 провести вертикальную линию связи до пересечения с горизонтальной линией связи из фронтальной проекции А2. Пересечение этих двух линий связи определит новое положение проекции точки А’2.

Соединив между собой новые проекции точек, получим В’2А’2 натуральную величину прямой ℓ, что является решением первой задачи на преобразование комплексного чертежа.

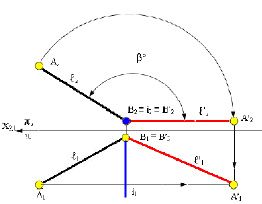
Для преобразования прямой ℓ общего положения в горизонталь, ее необходимо вращать около оси i, перпендикулярной П2 и проходящей через какую-либо точку прямой (рис. 5.17).

Рис. 5.17. Преобразование прямой линии общего положения
в горизонтальную (горизонталь) прямую

Для преобразования, заданной прямой, необходимо:

1) выбрать две точки А(А1А2) и В(В1В2), принадлежащие прямой ℓ;

2) провести ось вращения i (i1,i2) перпендикулярно П2 через точку В(В1В2) прямой ℓ(ℓ1, ℓ2);

3) при вращении прямой ℓ вокруг оси i точка В прямой остаётся неподвижной, так как принадлежит оси, и новое её положение будет с ней совпадать В2 ≡ В’2, а точка А будет вращаться по правилам, рассмотренным выше;

4) угол поворота β° точки А и ее фронтальной проекции А2 определяется между положением проекций А2В2 и А’2В’2, когда прямая ℓ займет положение, параллельное П1, ее фронтальная проекция ℓ’2 расположится перпендикулярно линиям связи.

Для определения положения проекции А’1 необходимо из А’2 провести вертикальную линию связи до пересечения с горизонтальной линией связи из А1. Пересечение этих двух линий связи определит новое положение проекции точки А’1. Соединив между собой новые проекции точек, получим В’1А’1 натуральную величину прямой ℓ, что является решением первой задачи на преобразование комплексного чертежа.

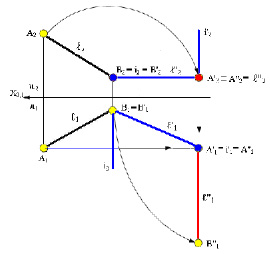
3адача 2. Преобразовать линию общего положения в проецирующую прямую (рис.5.18).

Рис. 5.18. Преобразование прямой линии общего положения
в горизонтально проецирующую

Вторую задачу на преобразование комплексного чертежа решать без решения первой задачи нельзя. Поэтому, если дана прямая общего положения, то для решения второй задачи необходимо выполнить два последовательных преобразования: вначале преобразовать ее в линию уровня (см. первую задачу), а затем линию уровня преобразовать в проецирующую (рис. 5.18, 5.19). Если линия уровня является фронталью, то ее можно преобразовать в горизонтально проецирующую прямую вращением около оси i’ перпендикулярной П2 (рис. 5.18). В рассматриваемом случае необходимо ось вращения провести через точку А’’. Во фронтальной плоскости проекций А’2 ≡ i’2 ≡ А’’2. Для определения нового положения точки В необходимо В’2 повернуть вокруг i’2 до положения В’’2. Соединив между собой новые проекции точек, получим В’’2А’’2, прямую перпендикулярную горизонтальной плоскости проекций (горизонтально проецирующую), что является решением второй задачи на преобразование комплексного чертежа.

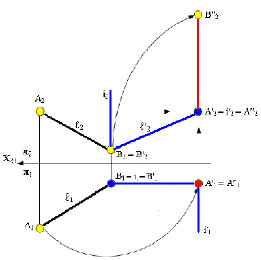
Рис. 5.19. Преобразование прямой общего положения
во фронтально-проецирующую

Если линия уровня является горизонталью, то ее можно преобразовать во фронтально проецирующую прямую вращением около оси i’ перпендикулярной П1 (рис. 5.19). В рассматриваемом случае необходимо ось вращения провести через точку А’’.

В горизонтальной плоскости проекций А’1 ≡ i’1 ≡ А’’1. Для определения нового положения точки В необходимо В’1 повернуть вокруг i’1 до положения В’’1. Соединив между собой новые проекции точек, получим В’’1А’’1, прямую перпендикулярную фронтальной плоскости проекций (фронтально проецирующую), что является решением второй задачи на преобразование комплексного чертежа.

Задача 3. Преобразовать чертеж так, чтобы плоскость общего положения Σ(ΔАВС) после поворота стала проецирующей (рис. 5.20).

Рис. 5.20. Преобразование плоскости Σ(ΔАВС) во фронтально-проецирующую

При решении таких задач необходимо знать, что две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Таким образом, если какую-либо прямую, принадлежащую плоскости Г, преобразовать в проецирующую, то плоскость Г тоже станет проецирующей.

Для того чтобы плоскость преобразовать во фронтально проецирующую, ее необходимо вращать вокруг оси i ⊥ П1, а в качестве вспомогательной линии уровня взять горизонталь. Для решения этой задачи можно использовать плоскость треугольника ΔАВС. Если плоскость Г(ΔАВС) вращать вокруг оси i ⊥ П1, то горизонталь (h), принадлежащая плоскости, может быть повернута в положение, перпендикулярное плоскости П2, при этом плоскость Г станет фронтально проецирующей (рис. 5.20).

Построения новой горизонтальной проекции А’1В’1С’1 треугольника ΔАВС в плоскости нужно провести горизонталь (А111), которую одним поворотом сделать проецирующей прямой. За ось вращения i можно принять горизонтально проецирующую прямую, которую для удобства решения, провести через точку (А), принадлежащую плоскости. В горизонтальной плоскости проекций П1 проекции исходного и нового положения точки А и оси вращения совпадают А1 ≡ А’1 ≡ i1. При повороте точек В1 и С1 вокруг i1 величина их угла поворота равна величине угла поворота горизонтальной проекции горизонтали h1. В результате поворота треугольник ΔА’В’С’ оказывается перпендикулярным П2 и поэтому его фронтальная проекция В’2А2С’2 вырождается в прямую линию, построение которой необходимо выполнить по правилам, рассмотренным выше.

Фронтальные проекции начального и нового положений точки А совпадают А2 ≡ А’2. Положения точек В2 и С2 определяются в пересечении вертикальных и горизонтальных линий связи соответствующих точек. Для определения положения В’2 необходимо из В’1провести вертикальную, а из В2 горизонтальную линии связи. Для определения положения С’2 необходимо из С’1 провести вертикальную, а из С2 горизонтальную линии связи. Новые положения точек плоскости Г во фронтальной плоскости проекций П2 находятся на одной прямой, что подтверждает условие перпендикулярности Г ⊥ П2 и решение третьей задачи на преобразование комплексного чертежа.

Для того чтобы плоскость Σ преобразовать в горизонтально проецирующую, её необходимо вращать вокруг оси i ⊥ П2, а в качестве вспомогательной линии уровня взять фронталь (рис. 5.21).

В качестве плоскости Σ можно использовать треугольник ΔDEK.

Если плоскость Σ (DEK) вращать вокруг оси i ⊥ П2, то фронталь (f), принадлежащая плоскости, может быть повернута в положение, перпендикулярное плоскости П1, при этом плоскость Σ станет горизонтально проецирующей (рис. 5.21).

Рис. 5.21. Преобразование плоскости Σ (ΔАВС) в горизонтально- проецирующую

Для построения новой горизонтальной проекции D’2E’2K’2 треугольника ΔDEK в плоскости нужно провести фронталь, которую одним поворотом сделать проецирующей прямой. За ось вращения i можно принять фронтально проецирующую прямую, которую для удобства решения, провести через точку (D), принадлежащую плоскости.

Во фронтальной плоскости проекций П2 проекции исходного и нового положения точки D и оси вращения совпадают D2 ≡ D’2 ≡ i2. При повороте точек E2 и K2 вокруг i2 величина их угла поворота равна величине угла поворота фронтальной проекции фронтали f2.

В результате поворота треугольник D’E’K’ оказывается перпендикулярным П1 и поэтому его горизонтальная проекция D’1 E11 K’2 вырождается в прямую линию, построение которой необходимо выполнить по правилам, рассмотренным выше.

Горизонтальные проекции начального и нового положений точки D совпадают D1 ≡ D’1. Положения точек E1 и K1 определяются в пересечении вертикальных и горизонтальных линий связи соответствующих точек. Для определения положения E’1 необходимо из E1 провести горизонтальную, а из E’2 вертикальную линии связи. Для определения положения К’1 необходимо из К1 провести горизонтальную, а из К’2 вертикальную линии связи. Новые положения точек плоскости Σ в горизонтальной плоскости проекций П1 расположены на одной прямой, что подтверждает условие перпендикулярности Σ ⊥ П1и решение третьей задачи на преобразование комплексного чертежа.

Источник