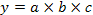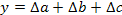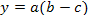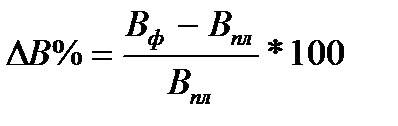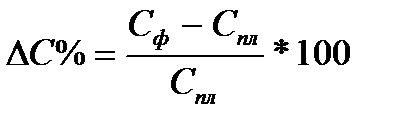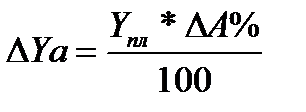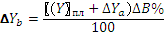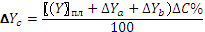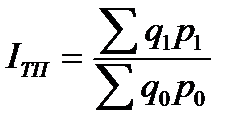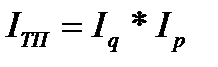Сущность способа абсолютных разниц

Способ абсолютных разниц

Вы будете перенаправлены на Автор24

Способ абсолютных разниц как разновидность метода элиминирования

Факторный анализ предполагает выявление факторов, влияющих на результирующий показатель, и определение степени их влияния. Одним из наиболее распространенных приемов определения степени влияния является элиминирование.

Элиминирование – это логический прием, позволяющий устранить влияние ряда факторов, выделив один фактор в качестве объекта изучения.

Сущность элиминирования состоит в следующем. Допустим, построена модель, в соответствии с которой результирующий показатель зависит от трех факторов. На практике все факторы могут меняться одновременно; может меняться два (а третий оставаться неизменным); может меняться лишь один (два остаются неизменными). Изменение факторов может обуславливать как рост показателя, так и его уменьшение. При этом изменение факторов может быть однонаправленным и разнонаправленным (например, численность персонала увеличилась – это должно способствовать увеличению выпуска, производительность труда снизилась – приводит к снижению выпуска, число рабочих дней увеличилось – способствует увеличению). При элиминировании последовательно рассматривается изменение только одного фактора (все остальные факторы предполагаются постоянными).

Метод абсолютных разниц (абсолютных отклонений), наряду с методом цепных подстановок, методом относительных отклонений и некоторыми другими, является способом осуществления элиминирования.

Методика способа абсолютных разниц

Способ абсолютных разниц применяется для определения степени влияния факторов на результирующий показатель в мультипликативных и мультипликативно-аддитивных моделях.

Мультипликативной называют модель, в которую факторы входят как члены произведения: $Y = a · b · c$.

Аддитивной называют модель, в которую факторы входят как члены алгебраической суммы (т.е. со знаком плюс или минус): $Y = a + b — c$.

Мультипликативно-аддитивная модель является смешанной моделью, объединяющей мультипликативную и аддитивную модели: $Y = a · (b + c)$.

Готовые работы на аналогичную тему

Таким образом, использование метода абсолютных разниц ограничено, он применим не для всех моделей. Но в силу распространенности моделей, для которых он предназначен, а также простоты самого метода, он широко применяется в анализе хозяйственной деятельности.

Сущность метода абсолютных разниц состоит в том, что величина влияния фактора определяется как произведение абсолютного прироста переменного фактора (анализируемого на данном шаге) на плановую (базовую) величину расположенных справа от него факторов и фактическую величину расположенных слева факторов.

Алгоритм расчета для мультипликативной модели, содержащей 4 фактора:

Определяем абсолютные отклонения каждого из факторов (отклонение фактического значения от планового):

Вычисляем влияние изменение факторов на результат:

Таким образом, на каждом шаге в произведении один из плановых показателей заменяется на абсолютное отклонение, а абсолютное отклонение, использованное на предыдущем шаге – на фактическое значение.

В смешанных моделях (мультипликативно-аддитивных) расчет производится несколько иначе. При вычислении влияния факторов, входящих в алгебраическую сумму, другие входящие в эту сумму факторы полностью исключаются из рассмотрения.

В целях контроля правильности вычислений необходимо проверить, чтобы сумма изменений, обусловленных каждым из анализируемых факторов, была равна общему изменению результирующего показателя. В выводах указывается, какое влияние (по направлению и объему) оказал каждый фактор.

Источник

Сущность и область применения элиминирования (способы: цепной подставки, абсолютных и относительных разниц, индексный)

Если между результативным и факторными показателями суще­ствует строгая функциональная зависимость, то для определения влияния факторов на изменение результативного показателя можно использовать прием элиминирования.

Элиминирование — это прием, при котором для определения влияния на изучаемый показатель каждого фактора в отдельности устраняется влияние всех факторов кроме одного, влияние которого на изменение результативного показателя и рассчитывается. Данный; прием исходит из того, что все факторы изменяются независимо друг от друга, что позволяет определить влияние каждого фактора на уро­вень результативного показателя в отдельности.

Можно выделить следующие основные способы элиминирования:

Рассмотрим каждый из способов подробнее.

Способ цепной подстановки. Данный прием является наи­более универсальным и используется для расчета влияния факторов во всех типах детерминированных факторных моделей.

Суть способа цепной подстановки заключается в последова­тельной замене планового или базисного значения каждого факторно­го показателя его фактической величиной отчетного периода. Данная замена называется подстановкой. Начинают замену с основного ко­личественного фактора, производят расчеты и из полученного резуль­тата вычитают предшествующий результат (до замены данного фактора). Полученная при этом разность и показывает искомую величину влияния данного фактора на изменение результативного показателя, так как все остальные факторные показатели принимаются одинако­выми по величине.

Алгоритм расчета влияния факторов на изменение результатив­ного показателя способом цепной подстановки включает следующие этапы.

1 этап. Построение факторной модели результативного пока­зателя:

где у — результативный показатель;

а,b,с — факторные показатели, имеющие с результативным пока­зателем мультипликативную зависимость.

2 этап. Определение абсолютного изменения результативного показателя:

базисное значение результативного показателя:у₀ = а₀ ∙ b₀ ∙ с₀;

фактическое значение результативного показателя: у₁ = а₁ ∙ b₁ ∙ c₁

3 этап. Расчет влияния факторов на изменение результативно­го показателя:

4 этап. Проведение балансовой увязки полученных результатов:

∆

5 этап. Формулирование выводов по результатам проведенного анализа.

При использовании способа цепной подстановки необходимо со­блюдать следующие правила.

1. Число подстановок всегда больше числа исходных факторов на 1.

2. Первая подстановка принимается на плановом или базовом уровне результативного показателя, последняя подстановка — на фактическом уровне результативного показателя.

3. Вначале учитывается влияние количественных факторов на из­менение результативного показателя, затем качественных факторов.

4. Если изменяются количественные факторы, то качественные; факторные показатели принимаются на уровне плана или базового периода.

5. Если изменяются качественные факторы, то количественные факторы принимаются на уровне фактического значения отчетного периода.

Способ абсолютных разниц. Данный способ применяется: для расчета влияния факторов на изменение результативного показателя в мультипликативных и смешанных мультипликативно-аддитивных моделях типа:

Суть способа абсолютных разниц заключается в том, что для расчета влияния фактора на изменение результативного показателя необходимо абсолютное изменение данного факторного показателя ум­ножить на фактические значения факторов, влияние которых уже рассмотрено, и плановые (базовые) значения факторов, влияние которых еще будет рассматриваться. Способ является модификацией способа цепной подстановки, и эффективнее его использовать, когда исходные данные содержат абсолютные отклонения факторных показателей.

Алгоритм расчета влияния факторов на изменение результативного показателя способом абсолютных разниц включает следующие этапы:

1 этап. Построение факторной модели результативного показателя:

где у — результативный показатель;

а, b, с- факторные показатели, имеющие с результативным пока­зателем мультипликативную зависимость.

2этап. Определение абсолютного изменения результативного показателя:

базисное значение результативного показателя:у₀ = а₀ ∙ b₀ ∙ с₀;

фактическое значение результативного показателя: у₁ = а₁ ∙ b₁ ∙ c₁

3 этап. Расчет влияния факторов на изменение результативно­го показателя:

4 этап. Проведение балансовой увязки полученных результатов:

∆

5 этап. Формулирование выводов по результатам проведенного анализа.

Способ относительных разниц. Данный способ применя­ется для расчета влияния факторов на изменение результативного по­казателя в мультипликативных и смешанных мультипликативно-аддитивных моделях типа:

Суть способа относительных разниц заключается в том, что для расчета влияния фактора на изменение результативного показате­ля необходимо относительное изменение данного факторного показа­теля умножить на относительные величины факторов, влияние кото­рых уже рассмотрено. Наиболее эффективно его применение в тех случаях, когда исходные данные содержат относительные отклонения факторных показателей, выраженные в процентах.

Алгоритм расчета влияния факторов на изменение результативного показателя способом относительных разниц включает следующие этапы:

1 этап. Построение факторной модели результативного пока­зателя:

где у — результативный показатель;

а, b, с- факторные показатели, имеющие с результативным пока­зателем мультипликативную зависимость.

2 этап. Определение абсолютного изменения результативного показателя:

базисное значение результативного показателя:у₀ = а₀ ∙ b₀ ∙ с₀;

фактическое значение результативного показателя: у₁ = а₁ ∙ b₁ ∙ c₁

3 этап. Определение относительного отклонения факторных показателей:

4 этап. Расчет влияния факторов на изменение результативно­го показателя:

Согласно этому правилу, для расчета влияния первого фактора необходимо базисную (плановую) величину результативного показателя умножить на относительный прирост первого фактора, выраженного в виде десятичной дроби.

Чтобы рассчитать влияние второго фактора, нужно к плановой (базисной) величине результативного показателя прибавить изменение его за счет первого фактора и затем полученную сумму умножить на относительный прирост второго фактора. Влияние третьего фактора определяется аналогично: к плановой величине результативного показателя необходимо прибавить его прирост за счет первого и второго факторов и полученную сумму умножить на относительный прирост третьего фактора и т.д.

5 этап. Проведение балансовой увязки полученных результатов:

∆

6 этап. Формулирование выводов по результатам проведенного анализа.

Индексный метод основан на относительных показателях динамики, пространственных сравнений, выполнения плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому, или по другому объекту).

С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.

Для примера возьмем индекс стоимости товарной продукции:

Он отражает изменение физического объема товарной продукции (q) и цен (р) и равен произведению этих индексов:

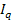
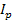
Чтобы установить, как изменилась стоимость товарной продукции за счет количества произведенной продукции и за счет цен, нужно рассчитать индекс физического объема и индекс цен .

Источник

Способ абсолютных разниц

Способ абсолютных разниц применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных моделях вида: Y=X₁*X₂*X₃*….X_n и моделях мультипликативно — аддитивного типа: Y=(a-b)*c; Y=a*(b-c)

И хотя его использование ограничено, благодаря своей простоте, он получил широкое применение в АХД.

При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста значения исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.

Отклонение от плана

Среднесписочная численность рабочих Среднегодовая выработка продукции одним рабочим, млн. руб. Количество отработанных дней одним рабочим за год Среднедневная выработка рабочего, тыс. руб. Средняя продолжитель­ность смены, час Среднечасовая выработка продукции одним рабочим, тыс. руб.

Алгоритм расчета для мультипликативной четырехфакторной модели валовой продукции выглядит следующим образом:

План по выпуску продукции в целом перевыполнен на 200 млн. руб. ( 600 – 400 ), в том числе за счет изменения:

1. количества рабочих ΔВП _чр = + 80
2. количества отработанных дней одним рабочим за год ΔВП _Д = +20
3. средней продолжительности рабочего дня ΔВП _П = — 31,25
4. среднечасовой выработки ΔВП _ЧВ = -131,25
5. ΔВП = ΔВП _чр + ΔВП _Д + ΔВП _П + ΔВП _ЧВ = + 80 +20 — 31,25 + 131,25 = +200

Всего: + 200 млн. руб.

Таким образом, с помощью способа абсолютных разниц получаются те же результаты, что и способом цепной подстановки . Здесь также необходимо следить за тем, чтобы алгебраическая сумма прироста результативного показателя за счет отдельных факторов равнялась его общему приросту:

Рассмотрим алгоритм расчета факторов этим способом в моделях мультипликативно-аддитивного вида. Для примера возьмем факторную модель прибыли от реализации продукции: П=V(Ц — C)

П– прибыль от реализации продукции;

V– объем реализации продукции;

Ц – цена единицы продукции;

С – себестоимость единицы продукции.

Прирост суммы прибыли за счет изменения:

1. объема реализации продукции: ΔП_v = ΔV(Ц пл — С пл )
2. цены реализации: ΔП ц = V ф х ΔЦ
3. себестоимости продукции: ΔПс = V _ф х (-ΔС)

Источник