Способы задания плоскости



Плоскость считается заданной; если из всех точек пространства можно выделить только те точки, которые принадлежат данной плоскости. Плоскость на чертеже может быть определена следующими способами (каждый из способов допускает переход к любому другому способу).
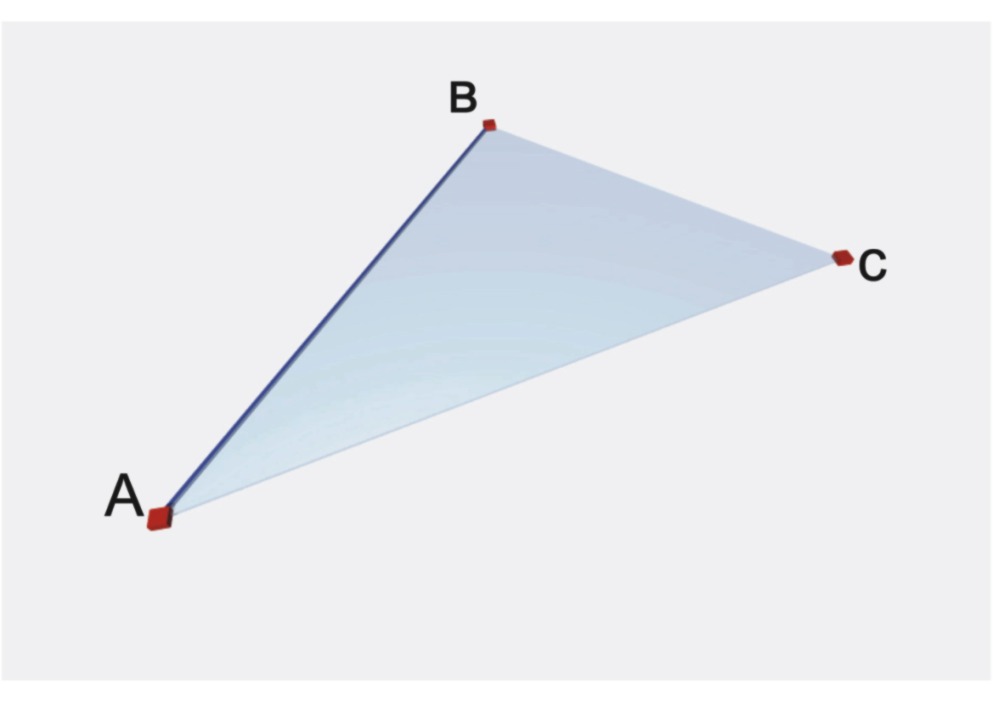
1. Тремя точками, не лежащими на одной прямой (рис. 4.1а).
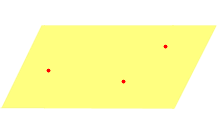
2. Прямой и точкой вне прямой (рис. 4.1б).
3. Двумя пересекающимися прямыми (рис. 4.1в).
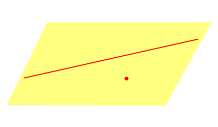
4. Двумя параллельными прямыми (рис. 4.1г).
5. Любой плоской фигурой-отсеком пространства (рис. 4.1д).
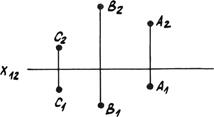
Рис. 4.1а. Три точки.
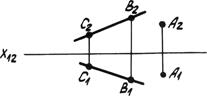
Рис. 4.1б. Прямая и точка.
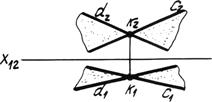
Рис. 4.1в. Пересекающиеся прямые.
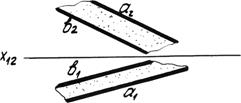
Рис. 4.1г. Параллельные прямые.
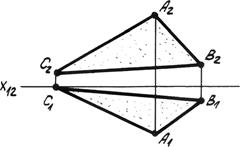
Рис. 4.1д. Фигура.
6. Следами плоскости (рис. 4.2).
Следы плоскости — это линии пересечения плоскости с плоскостями проекций.
Линия пересечения плоскости с плоскостью p1 называется горизонтальным следом плоскости Q1, с плоскостью p2-фронтальным следом Q2, с плоскостью p3-профильным следом Q3. Точки пересечения следов на осях проекций называются точками схода следов Qx, Qy, Qz.
Отрезки OQx , OQy , OQz, отсекаемые осями проекций, называют параметрами плоскости (рис. 4.2).
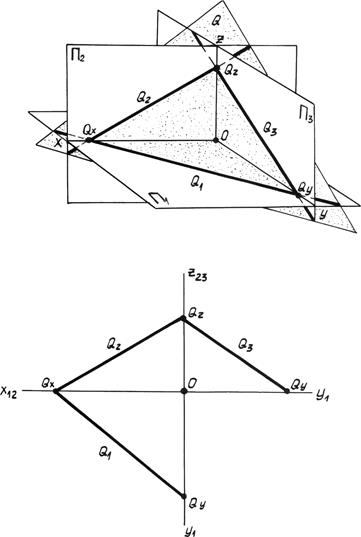
Рис. 4.2. Следы плоскости.
Источник
Чертежи и 3d визуализация по России!
Положение плоскости в пространстве определяется:
а) тремя точками, не лежащими на одной прямой линий, рис.1
б) прямой и точкой, взятой вне прямой, рис.2
в) двумя пересекающимися прямыми, рис.3
г) двумя параллельными прямыми. рис.4
Каждое из представленных на рис. 1— 4 заданий плоскости может быть преобразовано в другое из них. Например, проведя через точки А и В (рис. 1) прямую, мы получим задание плоскости, представленное на рис. 2: от него мы можем пе¬рейти к рис. 4, если через точку С проведем прямую, параллельную прямой АВ.
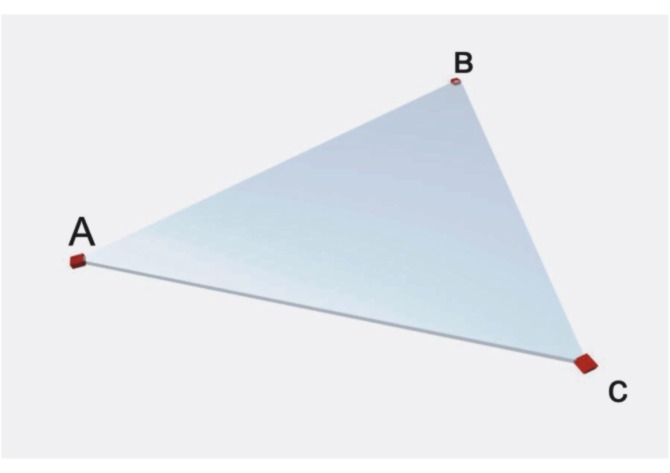
рис.1 рис.2
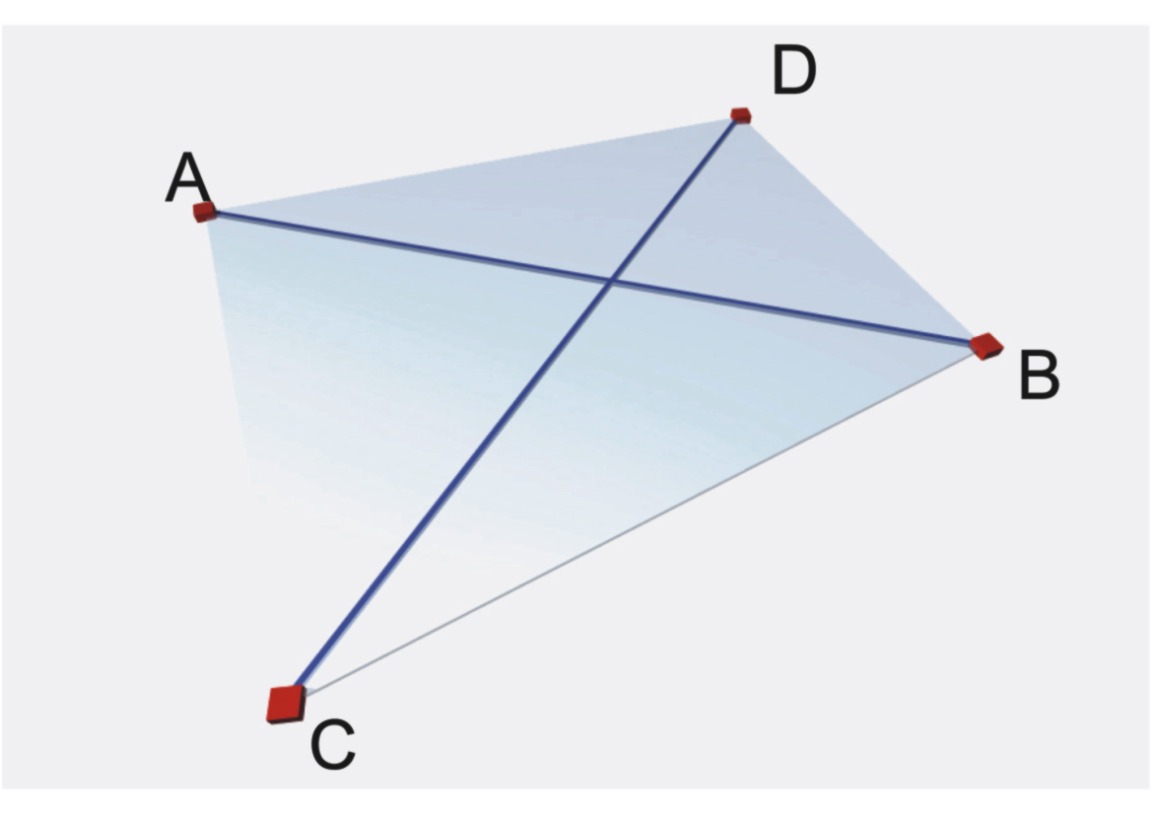
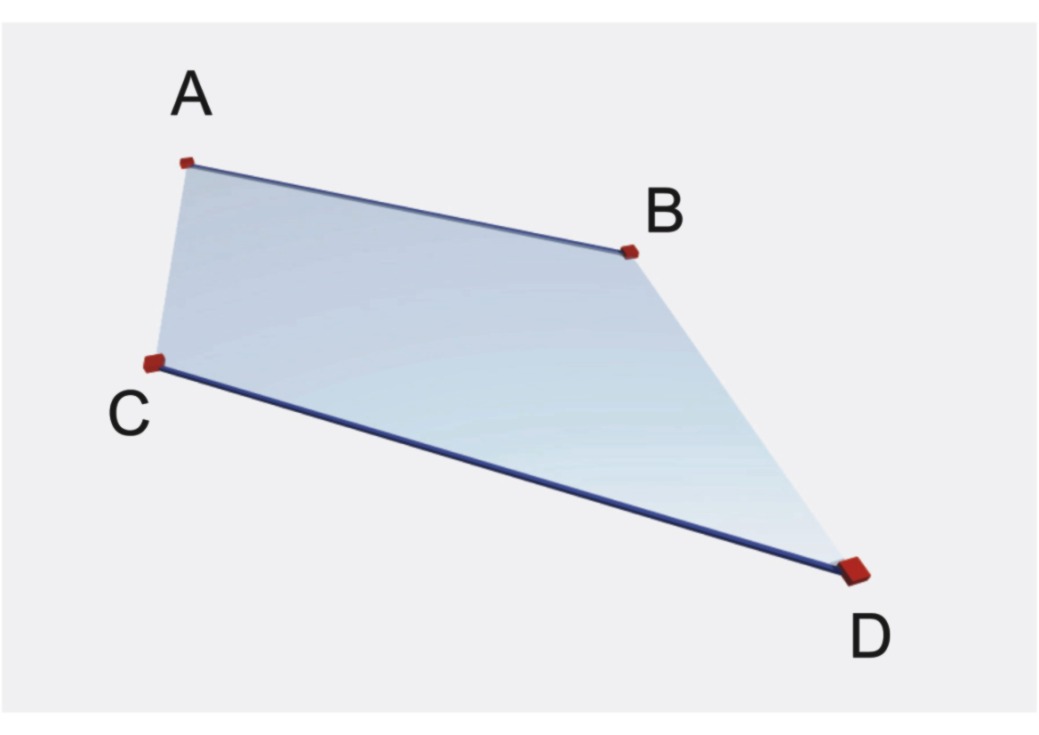
рис.3 рис.4
Важное замечание!
Многие студенты, изучающие начертательную геометрию или инженерную графику , сталкиваются с проблемой: вроде бы читаешь текст в учебнике, а все равно не понимаешь темы! Одна из причин этого – это то, что человек не мыслит образно. В чем заключается этот метод образного мышления? Да все просто, читая текст, представляйте себе «картинку» объекта (сцены). Ну, например, читая слово плоскость или прямая, кто вам мешает плоскость представить в виде ровного куска стекла (рис.5), а прямую как очень тонкую трубу без изгибов! И таких примеров можно привести миллион. Используя метод образного мышления, вы сможете не только научиться правильно решать задачи по начертательной геометрии или инженерной графике, но и ускорять процесс работы! Например, вам нужно построить по двум видам (вид спереди и сверху) аксонометрию детали. Используя метод образного мышления, вы представляете себе будущий объем детали, понимаете, что часть невидимых линий совершенно не обязательно простраивать (рис.6). В данном случае достаточно просто показать те линии, которые будут видны! Тем самым вы раза в полтора ускоряете свою работу – это очень помогает на экзаменах, когда вы делаете работу не только за себя, но и за друга – балбеса ).
Источник
Способы задания плоскости в пространстве
Все возможные способы задания плоскости в пространстве представлены в следующей таблице.
| Фигура | Рисунок | Тип утверждения и формулировка | |||||||||||||||||||||||||||||||||||||||||||||||
| Три различные точки | 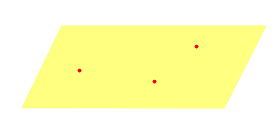 | ||||||||||||||||||||||||||||||||||||||||||||||||
| Прямая линия и точка, не лежащая на этой прямой | 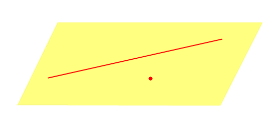 | ||||||||||||||||||||||||||||||||||||||||||||||||
| Две пересекающиеся прямые | 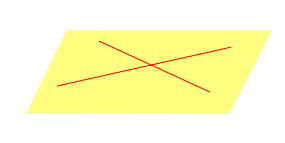 | ||||||||||||||||||||||||||||||||||||||||||||||||
| Две параллельные прямые | 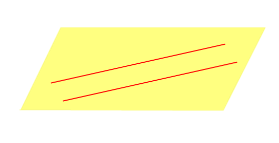 | ||||||||||||||||||||||||||||||||||||||||||||||||
| Прямая линия и точка, не лежащая на этой прямой | |||||||||||||||||||||||||||||||||||||||||||||||||
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
2. прямой линией и точкой, не принадлежащей этой прямой (рис. 4 2);
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
3. двумя пересекающимися прямыми (рис.43);
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
4. двумя параллельными прямыми (рис.44);
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.45).
С ледом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная a плоскость различают горизонтальный a П1, фронтальный a П2 и профильный a П3 следы.
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
Следы плоскости общего положения пересекаются попарно на осях в точках a x , a y , a z . Эти точки называются точками схода следов , их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.
Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.
Источник