Существует универсальный способ решения задач линейного программирования называемый

Решение задач линейного программирования

Решение происходит в три этапа:

1. Переход к КЗЛП. Любая ЗЛП вида ax ≤ b , ax ≥ b , ax = b ( F(X) → extr ) сводится к виду ax = b , F(X) → max ;
2. Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b , F(X) → max ;
3. Решение симплексным методом;

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Переход от задачи минимизации целевой функции к задаче максимизации

Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции: F*(X) = -F(X) . Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)) .
Проиллюстрируем этот факт графически:

F(x) → min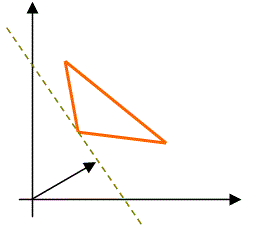

F(x) → max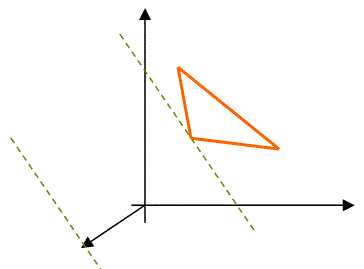

Для оптимизации функции цели используем следующие понятия и методы.
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).

Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).

Переменные x₁, …, x_m, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (x_m+1,…, x_n) называются небазисными или независимыми переменными.

Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных x_j≥0, что эквивалентно условию неотрицательности b_j≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел b_j есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.

Источник

1.3 Методы решения задач линейного программирования

1.3.1 Графический метод

Одним из методов решения задач линейного программирования является графический метод.

Рассмотрим задачу ЛП в стандартной форме записи:

Рассмотрим эту задачу на плоскости, т.е. при n = 2. Пусть система неравенств (**), (***) совместна (имеет хотя бы одно решение):

Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой a_i1x₁ + a_i2x₂ ≤ b_i . Условия не отрицательности определяют полуплоскости соответственно с граничными прямымиx₁ = 0; x₂ = 0.. Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых составляют решение данной системы. Совокупность этих точек называют многоугольником решений. Это может быть точка, отрезок, луч, замкнутый многоугольник, неограниченная многоугольная область.

Если в системе ограничений (**) — (***) n = 3, то каждое неравенство геометрически представляет полупространство трехмерного пространства, граничная плоскость которого a_i1x₁ + a_i2x₂ + a_i3x₃ ≤ b_i, а условия не отрицательности — полупространства с граничными плоскостями соответственно x_i = 0 (i = 1, 2, 3). Если система ограничений совместна, то эти полупространства, как выпуклые множества, пересекаясь, образуют в трехмерном пространстве общую часть, которая называется многогранником решений.

Пусть в системе (**) — (***) n > 3, тогда каждое неравенство определяет полупространство n-мерного пространства с граничной гиперплоскостью a_i1x₁ + a_i2x₂ + … + a_inx_n ≤ b_i i = 1, 2, …, т, а условия не отрицательности — полупространства с граничными гиперплоскостями x_j = 0, j = 1, 2, …, n.

Если система ограничений совместна, то по аналогии с трехмерным пространством она образует общую часть n-мерного пространства, называемую многогранником решений, так как координаты каждой его точки являются решением.

Таким образом, геометрически задача линейного программирования представляет собой отыскание такой точки многогранника решений, координаты которой доставляют линейной функции минимальное значение, причем допустимыми решениями служат все точки многогранника решений.

1.3.2 Симплекс-метод

В общем виде, когда в задаче участвуют N-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.

Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.

Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь — система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Для определенности предположим, что выбраны первые, идущие подряд, неизвестные x₁, x₂, . x₃. Тогда наша система уравнений может быть записана как:

К такому виду можно привести любую совместную систему, например, методом Гаусса. Правда, не всегда можно выражать через остальные первые r неизвестных (мы это сделали для определенности записи). Однако такие r неизвестных обязательно найдутся. Эти неизвестные (переменные) называются базисными, остальные свободными.

Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом, можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные x₁, x₂, . x_r, то решение <b₁, b₂, . b_r, 0, . 0> будет опорным при условии, что b₁, b₂, . b_r ≥ 0.

Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом.

Итак, симплексный метод вносит определенный порядок как при нахождении первого (исходного) базисного решения, так и при переходе к другим базисным решениям. Его идея состоит в следующем.

Имея систему ограничений, приведенную к общему виду, то есть к системе m линейных уравнений с n переменными (m 3 / 5 3 4 5 > Следующая > >>

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Решение задачи линейного программирования. Симплекс метод

Задача линейного программирования (ЗЛП) − это задача нахождения наибольшего (или наименьшего) значения линейной функции на выпуклом многогранном множестве.

Симплекс метод − это метод решения задачи линейного программирования. Суть метода заключается в нахождении начального допустимого плана, и в последующем улучшении плана до достижения максимального (или минимального) значения целевой функции в данном выпуклом многогранном множестве или выяснения неразрешимости задачи.

Рассмотрим следующую задачу линейного программирования в канонической форме:

(1)

(2)

(3)

где A-mxn-матрица, rank(A)=m, b− неотрицательный вектор столбец длины m (b∈ R m , b≥0), c − вектор строка длины n (c∈R n), x − вектор столбец длины n (x∈R n).

Определение 1. Допустимым планом или планом задачи линейного программирования (1)−(3) называется вектор , удовлетворяющим ограничениям (2)−(3).

Определение 2. Опорным планом задачи линейного программирования (1)−(3) называется план , если среди соотношений (2)−(3), которым он удовлетворяет как точным равенствам, имеется n линейно независимых.

Из определения 2 следует, что понятие опорный план совпадает с понятием вершины выпуклого многогранного множества, определяемого условиями (2)−(3).

Определение 3. Опорный план задачи линейного программирования (1)−(3) называется невырожденным , если число его положительных компонент в точности равен m.

Определение 4. Задача линейного программирования называется невырожденным , если все ее опорные планы невырождены.

Определение 5. Целевой функцией задачи линейного программирования (1)−(3) называется линейная функция cx, которую нужно максимизировать (в данном случае) на заданном выпуклом многогранном множестве (2)−(3).

Определение 6. Оптимальное решение или оптимальный план − это допустимый план, при котором целевая функция достигает своего максимума (в данном случае) на заданном выпуклом многогранном множестве (2)−(3).

Суть симплекс метода заключается в переходе от одного опорного плана к другому, до достижения оптимального плана или выяснения неразрешимости задачи. Неразрешимость задачи фиксируется, если допустимая область пуста или целевая функция неограничена сверху при максимизации целевой функции, или неограничена снизу, при минимизации целевой функции.

Симплекс метод включает в себя два этапа. Первый этап − нахождение начального допустимого плана. Второй этап − нахождение оптимального плана путем постепенного улучшения допустимого плана задачи.

Начнем рассмотрение метода со второго этапа. Мы будем предполагать, что ЗЛП невырождена (Определение 4).

Симплекс метод

Рассмотрим следующую задачу линейного программирования

(4)

(5)

(6)

где

Очевидно, что является опорным планом ЗЛП (4)-(6). Действительно, x 0 удовлетворяет уравнениям (5)-(6), и ровно m координат вектора x 0 положительны, а остальные нули.

Запишем ЗЛП (4)-(6) в векторном виде:

(4′)

(5′)

(6′)

где E−единичная матрица порядка m×m,

Разделим x на базисные и свободные компоненты (базисные компоненты − это положительные компоненты вектора, а свободные компоненты − это нулевые компоненты):

(7)

,.

(7′)

Тогда (5′) можно записать так:

.

(8)

.

(9)

(10)

Представим c в виде объединения базисных и свободных компонент:

,

(11)

,.

Тогда, учитывая (7), (10) и (11), получим

.

(12)

.

(12′)

Тогда (12) можно записать так:

.

(12»)

В выражении (12) ничего не изменится, если к правой части добавить нулевой элемент:

.

(13)

где − нулевая вектор-строка длины m.

.

(14)

Выражение (14) эквивалентно следующему выражению:

(14′)

или

,.

(14»)

Тогда (13) можно записать так:

.

(15)

.

(16)

Заметим, что первые m элементы вектора Δ и последние n−m элементы вектора x нулевые (;).

Посмотрев на выражение (16), замечаем, что если среди элементов есть отрицательный (например ), то целевую функцию cx можно увеличить, включая в базис соответствующий элемент ().

Учитывая (7′) перезапишем (5) следующим образом:

(17)

где −p-ый элемент вектора x, которую нужно ввести в базис (т.е сделать положительным).

Постепенно увеличивая из нуля нужно следить, чтобы новый вектор x удовлетворял уравнениям (17). Поэтому нужно уменьшить при , при этом нужно следить, чтобы не стал отрицательным. (В случае , увеличивается, а в случае , не изменяется).

Другими словами нужно решить систему линейных неравенств

(18)

,.

,.

(19)

Подставляя в (18), получим:

.

(20)

Тогда при имеем

а при имеем

.

Из вышеизложенного можно сформулировать следующие теоремы:

Теорема 1 (признак оптимальности опорного плана). Опорный план задачи (4)-(6) является оптимальным, если для любого j (j=1. n).

Теорема 2. Если для некоторого j=k, и среди чисел (i=1. m) нет положительных, целевая функция (4) задачи (4)-(6) не ограничена на множестве (5)-(6).

Теорема 3. Если опорный план x задачи (4)-(6) не вырожден и для некоторого j=k, и среди чисел (i=1. m) есть положительные, то существует опорный план x’ такой, что cx’ >cx.

Сформулированные теоремы позволяют проверить, является ли найденный опорный план оптимальным, и выявить целесообразность перехода к новому опорному плану.

Исследование опорного плана на оптимальность и вычислительный процесс удобнее вести, если первоначальные данные, полученные после определения исходного опорного плана записать в так называемой симплекс таблице.

В таблице 1, в первом столбце записвыаются базисные элементы текущего опорного плана. Во втором столбце записываются элементы правой части ограничений. С правой стороны второго столбца записываются элементы матрицы A. В нижней части таблицы записываются соответствующие элементы вектора Δ, а − значение целевой функции в данной точке.

Далее рассматривают элементы , . Если среди них нет отрицательных элементов, то данный план является оптимальным (Теорема 1).

Пусть . Тогда рассматривают . Если среди них нет положительных элементов, то задача неограничена сверху, т.е. неразрешима (теорема 2).

Пусть среди есть положительные элементы. Тогда вычисляют для всех тех i, для которых

Тогда из базиса выходит k-я переменная, а в базис входит p— я переменная, значение которой равно .

Далее делают исключение Гаусса для столбца p выбирая в качестве ведущего элемента . Т.е. обнуляются все элементы данного столбца, кроме . Для этого нужно сложить строку i со строкой k, умноженной на . Затем строку k делят на . В результате получают следующую симплекс таблицу:

,

,

,

.

Теперь рассматривают элементы , . Если среди них нет отрицательных элементов, то данный план является оптимальным, в противном случае поступают аналогично вышеизложенной процедуре.

Для решения задач линейного программирования онлайн, пользуйтесь калькулятором симплекс метод онлайн.

Метод искусственного базиса

Как было паказано выше, для задачи, записанной в канонической форме, если среди векторов столбцов матрицы A есть m единичных и линейно независимых, можно непосредственно указать опорный план. Однако для многих задач линейного программирования, записанных в канонической форме и имеющих опорные планы, среди векторов столбцов матрицы A не всегда есть m единичных и линейно независимых. Рассмотрим такую задачу:

Пусть требуется найти максимум функции

(21)

(22)

(23)

где и среди векторов

нет mединичных и линейно независимых.

Определение 7. Задача, состоящая в определении максимального значения функции

(24)

(25)

(26)

где M − некоторое достаточно больное положительное число (конкретное значение обычно не задается), называется расширенной задачей по отношению к (21)−(23).

Расширенная задача (24)−(26) имеет опорный план

,

(27)

где первы n элементы нули. Переменные называются искусственными . Векторы столбцы

(28)

образуют так называемый искусственный базис m-мерного векторного пространства.

Так как расширенная задача имеет опорный план, то ее решение можно найти симплекс методом.

Теорема 4. Если в оптимальном плане расширенной задачи (24)−(26) значения искусственных переменных , то является оптимальным планом задачи (21)−(23).

Таким образом, если в найденном оптимальном плане расширенной задачи, значения искусственных переменных равны нулю, то получен оптимальный план исходной задачи. Остановимся более подробно на нахождении решения расширенной задачи.

Значение целевой функции при опорном плане (27):

(29)

Значения вычисляются из выражения (14»):

(30)

Замечаем, что F(X) и состоят из двух независимых частей, одна из которых зависим от M, а другая − нет.

После вычисления F(X) и их значения, а также исходные данные расширенной задачи заносят в симплекс таблицу, как было показано выше. Разность заключается лишь в том, что данная таблица содержит на одну строку больше, чем обычная симплекс таблица. При этом в (m+1)-ю строку помещают коэффициенты, не содержащие M, а в (m+2)-ю строку − коэффициенты при M.

При переходе от одного опорного плана к другому, в базис вводят вектор, соответствующий наибольшему по абсолютной величине отрицательному числу (m+2) строки. Искусственный вектор, исключенный из базиса не имеет смысла вновь ввести в базис. При переходе к другому опорному плану, может случится так, что ни один из искусственных векторов из базиса не будет исключен. Пересчет симплекс таблицы при переходе от одного опорного плана к другому производят по обычным правилам симплекс метода (смотри выше).

Итерационный процесс ведут по m+2 строке до тех пор, пока элементы m+2 строки, соответствующие переменным не станут неотрицательными. При этом, если искусственные переменные исключены из базиса, то найденный план расширенной задачи отвечает некоторому опорному плану исходной задачи.

Если же не все искусственные переменные исключены из базиса и элемент m+2 строки, столбца x₀ отрицателен, то исходная задача не имеет решения.

Если же не все искусственные переменные исключены из базиса и элемент m+2 строки, столбца x₀ равен нулю, то опорный план исходной задачи является вырожденным и базис содержит минимум один из векторов искусственного базиса.

Если исходная задача содержит несколько единичных векторов, то их следует включить в искусственный базис.

Если в ходе итераций m+2 строка больше не содержит отрицательных элементов, то итерационный процесс продолжают с m+1 строкой, до тех пор, пока не найден оптимальный план расширенной задачи или не выявлен неразрешимость задачи.

Таким образом, процесс нахождения решения задачи линейного программирования (21)−(23) методом искусственного базиса включает следующие основные этапы:

• Составляют расширенную задачу (24)−(26).
• Находят опорный план расширенной задачи.
• Используя симплекс метод исключают искусственные векторы из базиса. В результате находят опорный план исходной задачи или фиксируют ее неразрешимость.
• Используя найденный опорный план ЗЛП (21)−(23), или находят оптимальный план исходной задачи, или устанавливают ее неразрешимость.

Для решения задач линейного программирования онлайн, пользуйтесь калькулятором симплекс метод онлайн.

Источник