Существует ровно 11 способов выбрать 3 предмета
а) Поставим сначала чёрную ладью. Это можно сделать 8 · 8 = 64 способами. Чтобы белая ладья её не била, надо поставить её в другие горизонталь и вертикаль, то есть свободных для неё горизонталей будет 8 — 1 = 7, и вертикалей тоже 8 — 1 = 7. То есть, поставить белую ладью при уже поставленной чёрной можно 7 · 7 = 49 способами. Так как на каждый из 64 способов поставить чёрную ладью будет 49 способов поставить белую, то всего способов поставить обе будет 64 · 49 = 3136.
б) Поставим сначала чёрного короля. Сколько способов тогда останется для постановки белого? Рассмотрим разные случаи:
Если чёрный король стоит в углу доски, то белого нельзя ставить на 4 клетки, то есть можно поставить на одну из 8·8 — 4 = 60 клеток. Углов в доске 4, то есть таких случаев, когда чёрный король стоит в углу, а белый его не бьёт, 4 · 60 = 240.
Дальше, если чёрный король стоит с краю доски (не в углу), то белого нельзя ставить на 6 клеток, то есть можно ставить на 64 — 6 = 58 клеток. На каждой из 4 сторон доски есть 8 — 2 = 6 клеток, где чёрный король будет стоять с краю, но не в углу, то есть всего таких вариантов растановки обоих королей будет 4 · 6 · 58 = 1392.
Наконец, если чёрный король стоит на внутренней клетке доски (они образуют квадрат со стороной 8 — 2 = 6, поэтому внутренних клеток будет 6 · 6 = 36), то белого можно поставить на одну из 64 — 9 = 55 клеток. Всего вариантов расстановки, где чёрный король стоит на внутренней клетке, будет 36 · 55 = 1980.
Итак, всего подходящих вариантов будет 240 + 1392 + 1980 = (200 + 40) + (1400 — 8) + (2000 — 20) = 1600 + 2000 + (40 — 20 — 8) = 3600 + 12 = 3612
Источник
13. Перестановки с повторениями
При перестановке букв в слове «толпа» получается P5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов», потому что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова»; всего перестановок в данном случае будет 
. Мы имеем здесь дело с перестановками с повторениями.
Общую задачу сформулируем следующим образом.
Имеется n элементов k различных типов: n1 элементов первого типа, n2 элементов второго типа, …, nk элементов k-го типа, 
. Сколько можно составить различных перестановок из этих элементов?
Число перестановок c повторениями обозначают 
. Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n2! перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом 
способами так, что она остаётся неизменной.
Число различных перестановок с повторениями, которые можно составить из данных элементов, равно
, (11.1) где 
.
Замечание. Отметим, что формула числа сочетаний из n элементов по k элементов совпадает с формулой для числа перестановок с повторениями из k элементов одного типа и n–k элементов другого типа:
.
Пример 11.1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?
Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k1=4 элементов первого типа (зеленых бус), k2=5 элементов второго типа (синих бус) и k3=6 элементов третьего типа (красных бус). По формуле (6) получаем
.
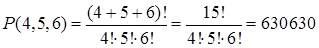
Пример 11.2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?
Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:
.
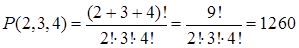
Пример 11.3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?
Решение. Камни можно переставлять P(5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем
.
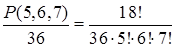
Пример 11.4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?
Решение. а) Буквы данного слова можно переставлять P(3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим
.
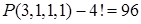
Б) Сначала расставляем согласные (3! способов). Для трёх букв «о» остаётся 4 места, и их можно расставить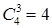 
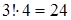
способами. Всего получаем 
способа.
11.1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?
Ответ: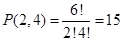 
.
11.2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?
Ответ: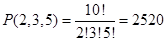 
.
11.3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?
Ответ: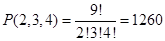 
.
11.4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?
Ответ: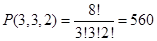 
.
11.5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?
Ответ: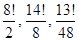 
.
11.6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?
Ответ: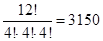 
.
11.7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?
Ответ: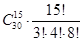 
.
11.8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?
Ответ: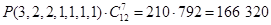 
.
11.9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?
Ответ: Гласные можно переставлять P(2,1,1)=12 способами, Аналогично, P(2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать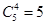 
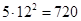
способами. Всего 
способов.
Источник
Урок «Комбинаторика» (9-11 класс)
Часто приходится иметь дело с задачами выбора элементов из некоторой совокупности и расположения этих элементов в определенном порядке. Поскольку в таких задачах речь идет о тех или иных комбинациях объектов, их называют комбинаторными задачами. Роль таких задач важна не только в математике, но и физике, химии, биологии, технике и экономике. Комбинаторные задачи приходится рассматривать при определении наиболее выгодных коммуникаций внутри города, при организации автоматической телефонной связи, при выявлении связей внутри сложных молекул, генетического кода, математической статистики и т. д.
Трудно переоценить значимость той роли, которую играет обучение методам решения комбинаторных задач в общеобразовательной школе. Освоение методов решения таких задач способствует развитию умственных способностей и математического кругозора ученика. Комбинаторные задачи несут широкие возможности для способов решения таких задач, которые могут служить как формы общих методов решения задач.
Для ознакомления первого правила комбинаторики-правила суммы мы предлагаем разбор следующей задачи:
Задача 1. На столе лежат 3 черных и 5 красных карандашей. Сколькими способами можно выбрать карандаш любого цвета?
Решение: Выбрать карандаш любого цвета можно 5+3=8 способами.
Правило суммы в комбинаторике:
Если элемент а можно выбрать m способами, а элемент в- n способами, причем любой выбор элемента а отличен от любого выбора элементов в, то выбор «а или в» можно сделать m + n способами.
Задача 2. В классе 10 учащихся занимаются спортом, остальные 6 учащихся посещают танцевальный кружок. 1)Сколько пар учащихся можно выбрать так, чтобы один из пары был спортсменом, другой танцором? 2)Сколько возможностей выбора одного ученика?
Решение: 1)Возможность выбора спортсменов 10, а на каждого из 10 спортсменов выборов танцора 6. Значит, возможность выбора пар танцора и спортсмена 10·6=60.
2) Возможность выбора одного ученика 10+6=16.
Рассмотрим решение задачи, через которое сформулируем новое правило – правило произведения, неоднократно используемое при изучении последующего материала.
Задача 1. Из города А в город В ведут 3 дороги. А из города В в город С ведут 4 дороги. Сколько путей, проходящих через В, ведут из А в С?
Решение: Можно рассуждать таким образом: для каждой из трех путей из А в В имеется четыре способа выбора дороги из В в С. Всего различных путей из А в С равно произведению 3·4, т.е. 12.
Задача 2. В школьной столовой имеются 2 первых, 5 вторых и 4 третьих блюд. Сколькими способами ученик может выбрать обед, состоящий из первых, вторых и третьих блюд?
Решение: Первое блюдо можно выбрать 2 способами. Для каждого выбора первого блюда существует 5 вторых блюд. Первые два блюда можно выбрать 2·5=10 способами. И, наконец, для каждой 10 этих выборов имеются четыре возможности выбора третьего блюда, т. е. Существует 2·5·4 способов составления обеда из трех блюд. Итак, обед может быть составлен 40 способами.
Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.
Рассмотрим на примере перестановку без повторений.
Задача: На полке лежат 3 книги. В каком порядке можно расставить эти книги?
Решение: Обозначим их буквами а, в, с. Эти книги можно расставить на полке по – разному:
авс, асв, вас, вса, сав, сва.
Каждое из этих расположений называют перестановкой из трех элементов. При решении этой задачи можно воспользоваться правилом умножения. Выбор первого места на полке три. Для каждого выбора первого места есть две возможности выбора второго места. Из трех книг один выбран для первого места. Остаются 2 остальные книги. Наконец, для каждого выбора первых, вторых мест только один выбор третьего места.
Опредление: Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке.
Число перестановок из n элементов обозначается символом Р n .
Пусть мы имеем n элементов. На первое место можно поставить любой из них всего п выборов. На второе место любой из оставшихся, т. е. n -1 выбор. На третьем месте любой из оставшихся после первых двух выборов, т. е. n -2 выбора и т. д. В результате получим: Р n = n ·( n -1)·( n -2)…2·1.
Если произведение обозначим 1·2·3…( n -1)· n = n !, то число всевозможных перестановок из к элементов вычисляется по формуле:
Сколькими способами можно расставить 7 бегунов на 7 дорожках?
Решение: Р 7 =1·2·3·4·5·6·7=5040 Ответ: 5040 способов.
Сколько различных пятизначных чисел можно составить из цифр 0, 1, 2, 3, 4, если цифры не повторяются?
Решение: Так как натуральное число не может начинаться с цифры 0, исключаем те числа, которые начинаются с цифры 0. Количество таких чисел
Р 5 – Р 4 = 1·2·3·4·5-1·2·3·4 = 120-24=96 Ответ: 96 чисел.
На собрание пришли 3 девочки и 4 мальчика. Сколькими способами можно их рассадить, если девочки хотят сидеть рядом?
Решение: Если рассмотреть девочек как одну, всего перестановок будет Р 5 . В каждой из полученных комбинаций можно выполнить Р 3 перестановок девочек. Искомое число перестановок:
Р 5 ·Р 3 = 5!·3!=1·2·3·4·5·1·2·3=720 Ответ: 720 способов.
Задача: Даны четыре различных шара: белый, зеленый, красный и синий. Их нужно поместить в 3 пустые ячейки. Сколько всего будет способов размещения шаров?
Решение: Сначала выпишем все варианты, которые начинаются с белого шара, затем – с зеленого и т. д.
бзк, бкз, бзс, бсз, бкс, бск.
збк, зкб, зсб, збс, зкс, зск.
кбз, кзб, ксб, кбс, кзс, ксз.
сбз, сзб, скб, сбк, скз, сзк.
Всего способов 24. В первую ячейку можно выбрать четырьмя способами. Во вторую – тремя, в третью – двумя. Всего способов 4·3·2=24. Каждую упорядоченную тройку, которую можно составить из четырех элементов, называют размещением из четырех элементов по три.
Определение: Размещением из n элементов по к (к≤ n ) называется любое множество, состоящее из любых к элементов, взятых в определенном порядке из данных n элементов.
Каждое множество при размещении отличается порядком элементов или их составом.
Число размещений из n элементов по к обозначают А n .
Первый элемент можно выбрать n способами, второй n -1 и последний к-й элемент n -(к-1) способами.
А n = n ( n -1)( n -2)… ( n -( k -1))
Учащиеся одного класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предметов.
Решение: Расписание на один день отличаются либо порядком следования предметов, либо самими предметами. Значит, здесь речь идет о размещении
из 8 элементов по 4.
А 8 = 8·7·6·5=1680 Ответ: 1680 способов.
Сколькими способами тренер может распределить 10 спортсменов, на эстафете 4·100 на первом, во втором, третьем и четвертом этапах?
Решение: А 10 = 10·9·8·7·=5040 Ответ: 50400 способов.
3. Сколько существует пятизначных телефонных номеров, в каждом из которых все цифры различны и первая цифра различна отнуля? 5
Решение: Число размещений из десяти элементов по пять – А 10 . Число размещений
начинающихся с цифры ноль – А 9 . Число телефонных номеров равно:
А 10 – А 9 =10·9·8·7·6 – 9·8·7·6 = 27216 Ответ: 27216 номеров.
Задача: На столе лежат 5 разноцветных карандашей. Сколько способов для выбора 3 из них?
Решение: Обозначим карандаши буквами а, в, с, d , е. Можно составить такие сочетания: авс, ав d , abe , acd , ace , ade , bcd , bce , bed , cde .
Всего: 10 способов.
Определение: Сочетанием из n элементов по к называется любое множество, составленное из к элементов, выбранных из данных n элементов.
Число сочетаний из n элементов по к обозначается С n .
В сочетаниях не имеет значения порядок элементов, сочетания отличаются составом элементов.
Допустим, имеется множество, содержащее n элементов, и из его элементов составлены
всевозможные сочетания по к элементов. Число таких сочетаний равно С n . В каждом сочетании можно выполнить Рк перестановок. В результате мы получим все размещения,
которые можно составить из n элементов по к. Их число равно А n .
Значит, А n = Cn · P к. Отсюда С n = А n
Умножим числитель и знаменатель, на ( n -к)!
1·2·3·…· k ·( n — k )! k !( n — k )!
Из 12 учеников нужно выбрать 3 ученика на улусный новогодний бал. Сколькими способами можно сделать этот выбор?
Решение: Каждый выбор отличается от другого хотя бы одним учеником. Значит, здесь речь идет о сочетаниях из 12 элементов по 3:
С 12 = 1·2·3·…·9·10·11·12 = 220 Ответ: 220 способов
В классе 10 девочек и 8 мальчиков. Нужно выбрать троих дежурных. Сколькими способами можно сделать этот выбор, если:
а) среди них должен быть 1 мальчик;
б) это могуть быть любые 3 ученика?
Решение: а) выбрать одного мальчика можно С 8 способами:
Выбрать из 10 девочек 2 дежурных можно С 10 способами:
Способов из 3 дежурных, среди которых 1 мальчик, всего:
С 8 ·С 10 = 8·45=360 Ответ: 360 способов.
б) любых 3 учеников из 18 учащихся можно выбрать
С 18 = 1·2·3…15·16·17·18 = 816 Ответ: 816 способов.
В корзине имеются 15 груш и 7 яблок. Нужно выбрать 5 груш и 3 яблока. Сколькими способами это можно сделать?
Решение: Способов выбора 5 груш:
С 15 = 1·2·…·10·11·12·13·14·15 = 360360 = 3003
Способов выбора 3 яблок:
Всего указанный выбор можно сделать С 15 ·С 7 способами:
С 15 ·С 7 = 3003·35=105105 Ответ: 105105 способов.
Сколькими способами можно расставить в ряд на одной полке 7 книг?
Сколькими способами можно выбрать трех человек на 3 различные должности из восьми кандидатов?
Из 11 футболистов нужно делегировать 3 человека. Сколькими способами это можно сделать?
Сколькими способами может разместиться семья из трех человек в четырехместном купе, если других пассажиров в купе нет?
На станции 7 запасных путей. Сколькими способами можно расставить на них 4 поезда?
Сколькими способами можно изготовить трехцветный флаг с горизонтальными полосами, если имеется материал 7 различных цветов?
На соревнованиях по легкой атлетике приехала команда из 12 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете 4 по 100 м на первом, втором, третьем и четвертом этапах?
Сколькими способами могут быть распределены первая, вторая и третья премии между 15 участниками конкурса?
Сколькими способами 6 учеников, сдающих зачет, могут занять места в кабинете, в котором стоят 20 одноместных столов?
Сколько четырехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр: а) 1, 3, 5, 7, 9; б) 0, 2, 4, 6, 8.
Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отличная от нуля?
В классе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать из них двоих для участия в математической олимпиаде?
Учащимся дали список из 10 книг, которые рекомендуются прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?
Из лаборатории в которой работают заведующий и 10 сотрудников, надо отправить 5 человек в командировку. Сколькими способами это можно сделать, если: а) заведующий лабораторией должен ехать в командировку; б) заведующий лабораторией должен остаться?
В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить 4 мальчиков и трех девочек. Сколькими способами это можно сделать?
В библиотеке читателю предложили на выбор из новых поступлений 10 книг и 4 журнала. Сколькими способами он может выбрать из них 3 книги и 2 журнала?
Для ремонта школы прибыла бригада, состоящая из 12 человек. Трех из них надо отправить на четвертый этаж, а четырех — на пятый этаж. Сколькими способами это можно сделать?
В отделе работают 5 ведущих и 8 старших научных сотрудников. В командировку надо послать двух ведущих и трех старших научных сотрудников. Сколькими способами может быть сделан выбор сотрудников, которых надо послать в командировку?
Встретились 11 футболистов и 6 хоккеистов, и каждый стал по одному разу играть с каждым в шашки.
а) сколько встреч было между футболистами?
б) сколько встреч было между хоккеистами?
в) сколько встреч было между футболистами и хоккеистами?
г) сколько встреч было всего?
20. Встретились несколько человек и стали здороваться друг с другом. Известно, что
рукопожатий было от 60 до 70. Сколько человек встретились, если известно, что:
а) каждый здоровался с каждым;
б) только один человек не здоровался ни с кем;
в) только двое не поздоровались между собой.
21. В классе 15 девочек и 13 мальчиков. Нужно выбрать двух дежурных по классу.
Сколькими способами это можно сделать: а) при условии, что пару обязательно
должны составить мальчик и девочка? б) без указанного условия?
22. В оперном театре 10 певцов и 8 певиц, а в опере по замыслу композитора 5 мужских и
3 женских партии. Сколько существует различных певческих составов для спектакля,
если известно, что:
а) все певицы и певцы прекрасно ладят между собой;
б) певцы А и Б ни за что не будут петь вместе;
в) 6 певцов накануне сорвал голос на футболе, и одной певице придется петь мужскую
23. В шахматном кружке занимаются 16 человек. Сколькими способами тренер может
выбрать из них для предстоящего турнира:
а) команду из 4 человек;
б) команду из четырех человек, указав при этом, кто из членов команды будет играть
на первой, второй, третьей и четвертой досках?
24. Сколькими способами из класса, где учатся 24 учащихся, можно выбрать:
а) двух дежурных;
б) старосту и помощника старосты.
25. Из 20 вопросов к экзамену Вова 12 вопросов выучил, 5 совсем не смотрел, а в
остальных что– то знает, а что- то нет. На экзамене в билете будет три вопроса.
а) сколько существует вариантов билетов?
б) сколько из них тех, в которых Вова знает все вопросы?
в) сколько из них тех в которых есть вопросы всех трех типов?
Источник
