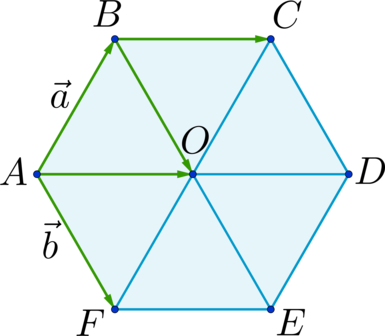
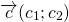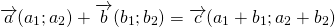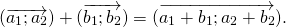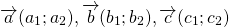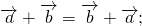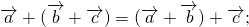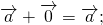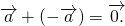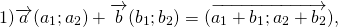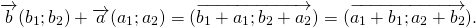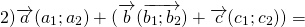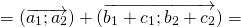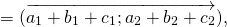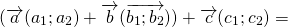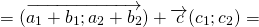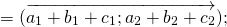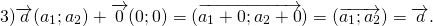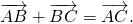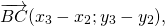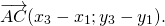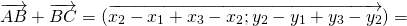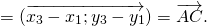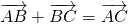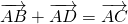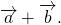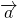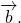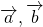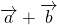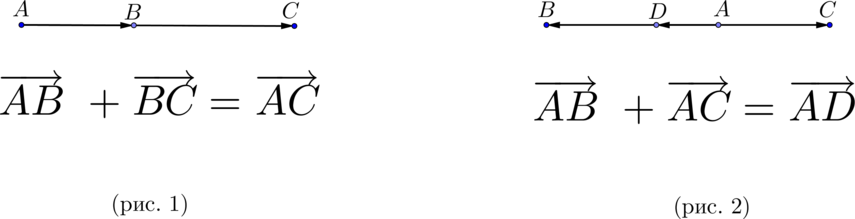Сложение векторов
Сумма векторов
Свойства сложения векторов:
Для любых векторов
3) свойство прибавления нулевого вектора:
4) сумма противоположных векторов равна нулевому вектору:
Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:
Так как соответствующие координаты равны, то эти векторы равны.
(О сложении векторов)
Каковы бы ни были точки A, B, C, имеет место векторное равенство:
Что и требовалось доказать.
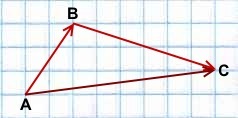
Правило треугольника построения суммы двух векторов
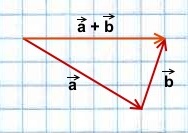
Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.
(то есть это правило следует из теоремы о сложении векторов).
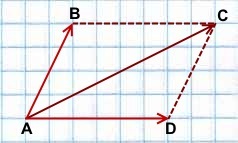
Правило параллелограмма построения суммы двух векторов
Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.
При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.
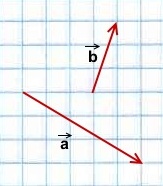
1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора
Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).
2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы
от общего начала.
Достроим на этих векторах параллелограмм.
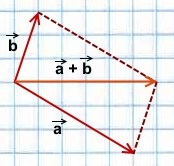
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.
1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.
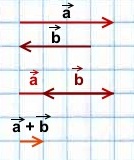
2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.
Фактически в обоих случаях мы используем правило треугольника сложения векторов:
от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.
Из неравенства треугольника следует ещё два свойства сложения векторов:
Источник
Векторы: правила сложения и вычитания
Вектор \(\overrightarrow
\(\blacktriangleright\) Два вектора коллинеарны, если они лежат на одной прямой или на двух параллельных прямых.
В противном случае векторы называются неколлинеарными.
\(\blacktriangleright\) Два коллинеарных вектора называются сонаправленными, если их направления совпадают.
Если их направления противоположны, то они называются противоположно направленными.
Правила сложения коллинеарных векторов:
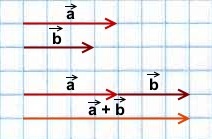
\(\blacktriangleright\) Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).
\(\blacktriangleright\) Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).
Правила сложения неколлинеарных векторов \(\overrightarrow \) и \(\overrightarrow\) :
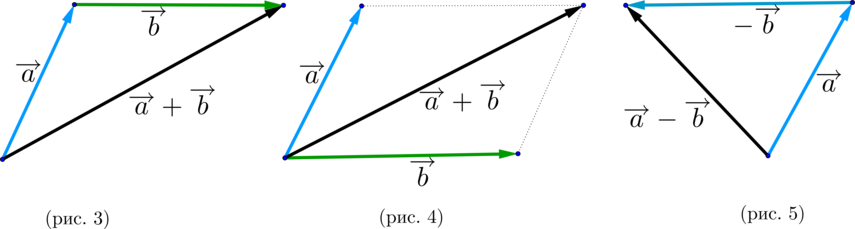
\(\blacktriangleright\) Правило треугольника (рис. 3).
\(\blacktriangleright\) Правило параллелограмма (рис. 4).
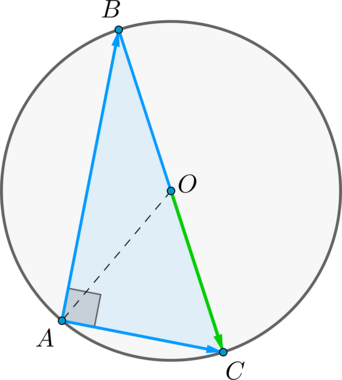
Дан прямоугольный треугольник \(ABC\) с прямым углом \(A\) , точка \(O\) – центр описанной около данного треугольника окружности. Координаты вектора \(\overrightarrow
Т.к. треугольник \(ABC\) — прямоугольный, то центр описанной окружности лежит на середине гипотенузы, т.е. \(O\) — середина \(BC\) .
Заметим, что \(\overrightarrow
Т.к. \(\overrightarrow
Значит, сумма координат вектора \(\overrightarrow
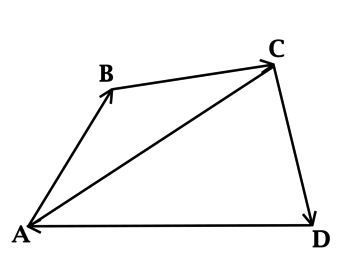
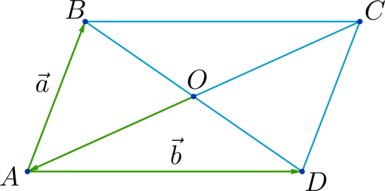
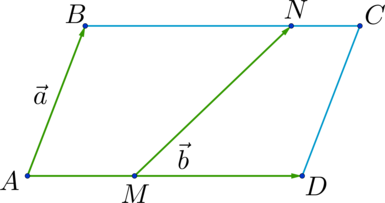
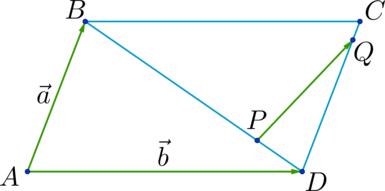
\(ABCD\) – четырёхугольник, на сторонах которого отложены векторы \(\overrightarrow
\(\overrightarrow
\(\overrightarrow
Нулевой вектор имеет длину, равную \(0\) .
Вектор можно воспринимать как перемещение, тогда \(\overrightarrow
При такой трактовке становится очевидным, что \(\overrightarrow
\[\begin
\(\Rightarrow\) \(x = \frac<7><10>\) , \(y = \frac<1><5>\) \(\Rightarrow\) \(x\cdot y = 0,14\) .
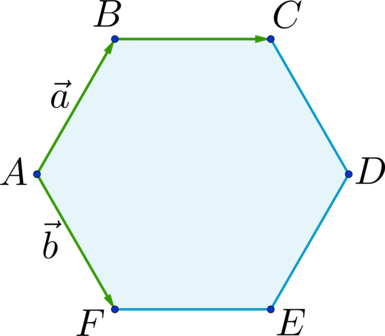
Отрезки \(AD\) , \(BE\) и \(CF\) пересекаются в точке \(O\) и делятся этой точкой пополам. \(BC \parallel AD\) и \(ABCO\) – параллелограмм; \(AF \parallel BE\) и \(ABOF\) – параллелограмм \(\Rightarrow\) \[\overrightarrow
Старшеклассники, которые готовятся к сдаче ЕГЭ по математике и при этом рассчитывают на получение достойных баллов, обязательно должны повторить тему «Правила сложения и вычитания нескольких векторов». Как видно из многолетней практики, подобные задания каждый год включаются в аттестационное испытание. Если у выпускника вызывают трудности задачи из раздела «Геометрия на плоскости», к примеру, в которых требуется применить правила сложения и вычитания векторов, ему обязательно стоит повторить или вновь разобраться в материале, чтобы успешно сдать ЕГЭ.
Образовательный проект «Школково» предлагает новый подход в подготовке к аттестационному испытанию. Наш ресурс выстроен таким образом, чтобы учащиеся смогли выявить наиболее сложные для себя разделы и восполнить пробелы в знаниях. Специалисты «Школково» подготовили и систематизировали весь необходимый материал для подготовки к сдаче аттестационного испытания.
Для того чтобы задачи ЕГЭ, в которых необходимо применить правила сложения и вычитания двух векторов, не вызывали затруднений, мы рекомендуем прежде всего освежить в памяти базовые понятия. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».
Если вы уже вспомнили правило вычитания векторов и основные определения по данной теме, предлагаем закрепить полученные знания, выполнив соответствующие упражнения, которые подобрали специалисты образовательного портала «Школково». Для каждой задачи на сайте представлен алгоритм решения и дан правильный ответ. В теме «Правила сложения векторов» представлены различные упражнения; выполнив два-три сравнительно легких задания, учащиеся могут последовательно переходить к более сложным.
Оттачивать собственные навыки по таким, например, заданиям, как задачи на координатной плоскости, школьники имеют возможность в режиме онлайн, находясь в Москве или любом другом городе России. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
Источник