Структура данных stack имеет способ организации fifo

Национальная библиотека им. Н. Э. Баумана
Bauman National Library

Персональные инструменты

FIFO (First In First Out)

FIFO (англ. First In First Out ) является аббревиатурой для «первый пришел, первый ушел», способа организации и управления буфером данных, где сначала обрабатывается самая старая (первая) запись, или ‘голова’ очереди. Она аналогична обработке очереди (первым пришел, первым обслужен (ПППО)): где люди покидают очередь в том порядке, в котором они прибывают.

ПППО — также жаргонный термин для алгоритма FIFO планирования операционной системы, которая дает каждому процессу время CPU (центрального процессора) в том порядке, в каком он потребовал.

Противоположностью FIFO является LIFO (Last In First Out), «последним пришел, первым ушел», где самая молодая запись или «вершина стека» обрабатывается в первую очередь. [1]

Очередь с приоритетами не является ни FIFO, ни LIFO, но может принять подобное поведение временно или по умолчанию.

Теория массового обслуживания охватывает эти методы для обработки структур данных, а также взаимодействия между строгими FIFO очередями.

Содержание

Информатика

Структура данных

В зависимости от прикладной программы, буфер FIFO может быть реализован в виде аппаратного регистра сдвига, или с использованием различных структур памяти, обычно циклическим буфером или одним из видов списков.

Есть несколько эффективных реализаций очередей FIFO. Эффективной реализацией является та, которая может выполнять операции — добавление в очередь (enqueuing) и извлечение из очереди (dequeuing) — за время O(1) .

• Связанный список
  • У двусвязного списка операции вставки и удаления на обоих концах занимают O (1) времени, так что это естественный выбор для очередей.
  • Простой связный список имеет эффективную вставку и удаление только на одном конце. Тем не менее, небольшая модификация — по поддержанию указателя на последний узел в дополнение к первому — позволит реализовать эффективную очередь.
• Двусторонняя очередь, или очередь с двусторонним доступом, (double-ended queue), реализованная с использованием модифицированного динамического массива.

Реализация

Следующий код показывает реализацию связанного списка FIFO на языке C++. На практике, существует целый ряд реализаций списка, в том числе популярных макросов Unix-систем C sys/queue.h или шаблона стандартной библиотеки C++ std :: list, устраняя необходимость в реализации структуры данных с нуля.

Первоочередность головы или хвоста очереди

Концы очереди FIFO часто называют головой и хвостом. К сожалению, существует спор относительно этих терминов:

• По мнению многих людей предметы должны входить в конец очереди (в хвост), и оставаться в очереди, пока они не достигнут начала очереди (головы) и покинуть очередь оттуда. Эта точка зрения оправдана по аналогии с очередями людей, ожидающих своего обслуживания в передней и задней части очереди (как и в приведенном выше примере).
• Другие люди считают, что элементы входят в очередь в голове и покидают её в хвосте, по аналогии с пищей, проходящей через змею. Очереди написанные таким образом появляются в тех местах, которые можно рассматривать как авторитетные, например, такие как операционная система Linux.

Программирование работы диска

Дисковые контроллеры могут использовать очередь FIFO в качестве алгоритма планирования работы диска для определения порядка обслуживания запросов ввода/вывода.

Коммуникации и сети

Сетевые мосты, коммутаторы и маршрутизаторы, используемые в компьютерных сетях используют FIFO для хранения пакетов данных на пути к их следующему месту назначения. Как правило, по меньшей мере, одна структура FIFO используется за сетевое соединение. Некоторые устройства имеют несколько FIFO для одновременного и независимого массового обслуживания различных типов информации.

Электроника

FIFO широко используются в электронных схемах для буферизации и управления потоком между аппаратным и программным обеспечением. В своей аппаратной форме, в первую очередь FIFO состоит из набора операций чтения и записи указателей, систем хранения данных и логики управления. Хранение может быть статическим оперативным запоминающим устройством (ОЗУ), триггерами или любой другой подходящей формой хранения. Для FIFO нетривиального размера обычно используется двухпортовый SRAM, где один порт предназначен для записи, а другой для чтения.

Синхронный FIFO это такой FIFO, где один и тот же тактовый сигнал используется как для чтения, так и для записи. Асинхронный FIFO использует различные тактовые сигналы для чтения и записи. Асинхронные FIFO вводят проблемы метастабильности. Общая реализация асинхронного FIFO использует код Грея (или любой блок кода расстояния) для чтения и записи указателей для обеспечения надежной генерации флага. Еще одно примечание, касающееся генерации флага, в том, что надо обязательно использовать арифметические операции над указателями, чтобы создать флаги для реализации асинхронного FIFO. С другой стороны, можно использовать либо подход, который называется «дырявое ведро», или арифметические операции над указателями для создания флагов в реализациях синхронных FIFO.

Примеры флагов состояния FIFO включают в себя: полный, пустой, почти полный, почти пустой, и т.д.

Первый известный FIFO, реализованный в электронике, был сделан Питером Алфке в 1969 году в Fairchild Semiconductors [2] . Питер Алфке позже стал директором Xilinx.

Очередь FIFO полна/пуста

Аппаратный FIFO используется для целей синхронизации. Он часто реализуется в виде круговой очереди, и, таким образом, имеет два указателя:

1. Указатель чтения/Регистр адреса чтения
2. Указатель записи/Регистр адреса записи

Операции чтения и записи адреса изначально находятся на первой позиции памяти и очередь FIFO пуста.

Очередь FIFO пуста

Когда регистр адреса чтения достигает регистра адреса записи, FIFO вызывает сигнал «Пуст».

Очередь FIFO полна

Когда регистр адреса записи достигает регистра адреса чтения, то FIFO запускает сигнал «Полон».

В обоих случаях, адреса чтения и записи в конечном итоге равны. Для того, чтобы различать эти две ситуации, есть простое и надежное решение — нужно добавить один дополнительный бит для каждого адреса чтения и записи, который инвертируется каждый раз, когда адрес переносится. При этом созданы условия неоднозначности:

1. Когда регистр адреса чтения равен регистру адреса записи, то FIFO пуст.
2. Когда наименее значимый бит адреса чтения равен наименее значимому биту адреса записи и дополнительные старшие значащие биты различны, FIFO полон.

Источник

Структуры данных. Неформальный гайд

Конечно, можно быть успешным программистом и без сакрального знания структур данных, однако они совершенно незаменимы в некоторых приложениях. Например, когда нужно вычислить кратчайший путь между двумя точками на карте, или найти имя в телефонной книжке, содержащей, скажем, миллион записей. Не говоря уже о том, что структуры данных постоянно используются в спортивном программировании. Рассмотрим некоторые из них более подробно.

Очередь

Итак, поздоровайтесь с Лупи!

Лупи обожает играть в хоккей со своей семьей. И под “игрой”, я подразумеваю:

Когда черепашки залетают в ворота, их выбрасывает на верх стопки. Заметьте, первая черепашка, добавленная в стопку — первой ее покидает. Это называется Очередь. Так же, как и в тех очередях, что мы видим в повседневной жизни, первый добавленный в список элемент — первым его покидает. Еще эту структуру называют FIFO (First In First Out).

Как насчет операций вставки и удаления?

После такой веселой игры в хоккей, Лупи делает для всех блинчики. Она кладет их в одну стопку.

Когда все блинчики готовы, Лупи подает их всей семье, один за одним.

Заметьте, что первый сделанный ею блинчик — будет подан последним. Это называется Стек. Последний элемент, добавленный в список — покинет его первым. Также эту структуру данных называют LIFO (Last In First Out).

Добавление и удаление элементов?

Вы когда-нибудь видели башню плотности?

Все элементы сверху донизу расположились по своим местам, согласно их плотности. Что случится, если бросить внутрь новый объект?

Он займет место, в зависимости от своей плотности.

Примерно так работает Куча.

Куча — двоичное дерево. А это значит, что каждый родительский элемент имеет два дочерних. И хотя мы называем эту структуру данных кучей, но выражается она через обычный массив.
Также куча всегда имеет высоту logn, где n — количество элементов

На рисунке представлена куча типа max-heap, основанная на следующем правиле: дочерние элементы меньше родительского. Существуют также кучи min-heap, где дочерние элементы всегда больше родительского.

Несколько простых функций для работы с кучами:

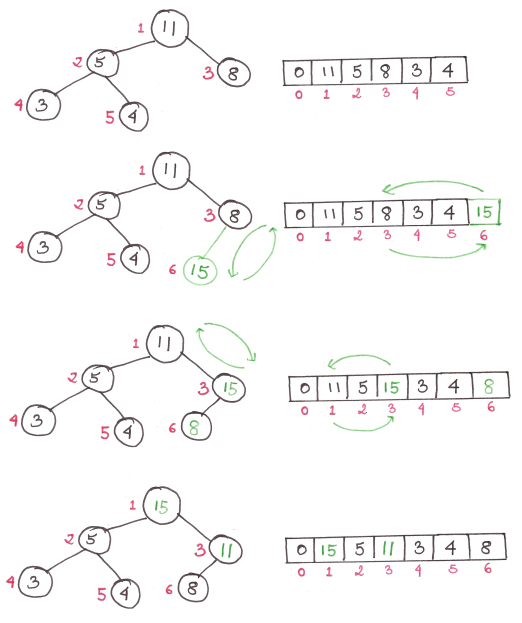
Добавление элемента в существующую кучу
Для начала, мы добавляем элемент в самый низ кучи, т.е. в конец массива. Затем мы меняем его местами с родительским элементом до тех пор, пока он не встанет на свое место.

Алгоритм:

1. Добавляем элемент в самый низ кучи.
2. Сравниваем добавленный элемент с родительским; если порядок верный — останавливаемся.
3. Если нет — меняем элементы местами, и возвращаемся к предыдущему пункту.

Код:

Максимальное количество проходов цикла while равно высоте дерева, или logn, следовательно, трудоемкость алгоритма — O(logn).

Извлечение максимального элемента кучи
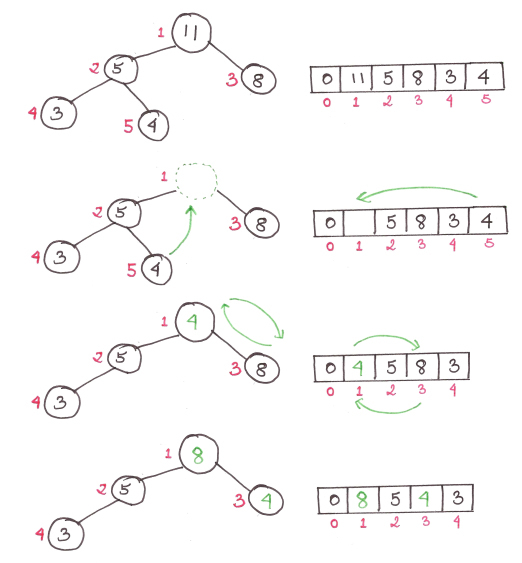
Первый элемент в куче — всегда максимальный, так что мы просто удалим его (предварительно запомнив), и заменим самым нижним. Затем мы приведем кучу в правильный порядок, используя функцию:

Алгоритм:

1. Заменить корневой элемент самым нижним.
2. Сравнить новый корневой элемент с дочерними. Если они в правильном порядке — остановиться.
3. Если нет — заменить корневой элемент на одного из дочерних (меньший для min-heap, больший для max-heap), и повторить шаг 2.

И вновь максимальное количество вызовов функции maxHeapify равно высоте дерева, или logn, а значит трудоемкость алгоритма — O(logn).

Делаем кучу из любого рандомного массива
Окей, есть два пути сделать это. Первый — поочередно вставлять каждый элемент в кучу. Это просто, но совершенно неэффективно. Трудоемкость алгоритма в этом случае будет O(nlogn), т.к. функция O(logn) будет выполняться n раз.

Более эффективный способ — применить функцию maxHeapify для ‘под-кучи’, от (currSize/2) до первого элемента.

Сложность получится O(n), и доказательство этого утверждения, к сожалению, выходит за рамки данной статьи. Просто поймите, что элементы, находящиеся в части кучи от currSize/2 до currSize, не имеют потомков, и большинство образованных таким образом ‘под-куч’ будут высотой меньше, чем logn.

Действительно, зачем это все?

Кучи нужны для реализации особого типа сортировки, называемого, как ни странно, “сортировка кучей”. В отличие от менее эффективных “сортировки вставками” и “сортировки пузырьком”, с их ужасной сложностью в O(n 2 ), “сортировка кучей” имеет сложность O(nlogn).

Реализация до неприличия проста. Просто продолжайте последовательно извлекать из кучи максимальный (корневой) элемент, и записывайте его в массив, пока куча не опустеет.

Чтобы обобщить все вышесказанное, я написала несколько строчек кода, содержащего функции для работы с кучей, а для фанатов ООП оформила все в виде класса.

Легко, не правда ли? А вот и празднующая Лупи!

Лупи хочет научить своих детишек различать фигуры и цвета. Для этого она принесла домой огромное количество разноцветных фигур.

Через некоторое время черепашки окончательно запутались

Поэтому она достала еще одну игрушку, чтобы немного упростить процесс

Стало намного легче, ведь черепашки уже знали, что фигуры рассортированы по форме. А что, если мы пометим каждый столб?

Черепашкам теперь нужно проверить столб с определенным номером, и выбрать из гораздо меньшего количества фигурок нужную. А если еще и для каждой комбинации формы и цвета у нас отдельный столб?

Допустим, номер столба вычисляется следующим образом:

Фиолетовый треугольник
ф+и+о+т+р+е = 22+10+16+20+18+6 = Столб 92

Красный прямоугольник
к+р+а+п+р+я = 12+18+1+17+18+33 = Столб 99

Мы знаем, что 6*33 = 198 возможных комбинаций, значит нам нужно 198 столбов.

Назовем эту формулу для вычисления номера столба — Хеш-функцией.

(с кириллицей немного сложнее, но я оставил так для простоты. — прим.пер.)

Теперь, если нам нужно будет узнать, где хранится розовый квадрат, мы сможем вычислить:

Это пример хеш-таблицы, где местоположение элементов определяется хеш-функцией.
При таком подходе время, затраченное на поиск любого элемента, не зависит от количества элементов, т.е. O(1). Другими словами, время поиска в хеш-таблице — константная величина.

Ладно, но допустим мы ищем “карамельный прямоугольник” (если, конечно, цвет “карамельный” существует).

вернет нам 99, что совпадает с номером для красного прямоугольника. Это называется “Коллизия”. Для разрешения коллизии мы используем “Метод цепочек”, подразумевающий, что каждый столб хранит список, в котором мы ищем нужную нам запись.

Поэтому мы просто кладем карамельный прямоугольник на красный, и выбираем один из них, когда хеш-функция указывает на этот столб.

Ключ к хорошей хеш-таблице — выбрать подходящую хеш-функцию. Бесспорно, это самая важная вещь в создании хеш-таблицы, и люди тратят огромное количество времени на разработку качественных хеш-функций.
В хороших таблицах ни одна позиция не содержит более 2-3 элементов, в обратном случае, хеширование работает плохо, и нужно менять хеш-функцию.

Еще раз, поиск, не зависящий от количества элементов! Мы можем использовать хеш-таблицы для всего, что имеет гигантские размеры.

Хеш-таблицы также используются для поиска строк и подстрок в больших кусках текста, используя алгоритм Рабина-Карпа или алгоритм Кнута-Морриса-Пратта, что полезно, например, для определения плагиата в научных работах.

На этом, думаю, можно заканчивать. В будущем я планирую рассмотреть более сложные структуры данных, например Фибоначчиеву кучу и Дерево отрезков. Надеюсь, этот неформальный гайд получился интересным и полезным.

Переведено для Хабра запертым на чердаке программистом.

Источник