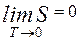Статистический вес это число способов

Статистический вес

Статистический вес — физическая величина, определяющая в квантовой механике и квантовой статистике количество различных квантовых состояний системы с одинаковой энергией (синоним: кратность вырождения энергетического уровня). В статистической физике и термодинамике статистическим весом называют количество способов (микросостояний системы), которыми может быть реализовано данное макроскопическое состояние статистической системы. Статистический вес обычно обозначается символами Γ, g, w, W или Ω.

По вышеприведённому определению, статистический вес является безразмерным целым числом, большим или равным единице, w ⩾ 1 . Иногда статвес называют термодинамической вероятностью, хотя необходимо отметить, что вероятность обычно определяется как действительное число в интервале от 0 до 1.

При рассмотрении квантовых систем с непрерывным спектром энергии под статистическим весом обычно понимают количество квантовых состояний, приходящихся на определённый энергетический интервал. В таком определении статвес имеет размерность обратной энергии.

В квазиклассическом приближении мерой статистического веса служит фазовый объём системы, приходящийся на определённый интервал энергии. Если система имеет n степеней свободы, то фазовый объём и соответствующий статистический вес выражается в единицах hn, где h — постоянная Планка.

Энтропия S системы и её статистический вес связаны соотношением Больцмана: S = k ln w (здесь k — постоянная Больцмана).

Статистический вес, определённый через фазовый объём или число микросостояний, является мультипликативной физической величиной: если система состоит из двух невзаимодействующих подсистем со статвесами w1 и w2, то общий статистический вес системы W = w1w2.

Источник

Понятие статистического веса

Чтобы пояснить понятие статистического веса, рассмотрим способы, которыми молекулы газа могут распределяться между двумя половинами сосуда, в котором заключен газ. Пусть общее число молекул равно N. В качестве характеристики состояния газа примем число молекул, находящихся в левой половине сосуда, которое мы обозначим буквой n (соответственно число молекул в правой половине сосуда будет равно N — n). Состояние отдельной молекулы будем характеризовать указанием на то, в какой из половин сосуда она находится. Такое описание состояния газа и состояний отдельных молекул является, конечно, далеко не полным. Однако оно достаточно для того, чтобы выяснить на этом примере характерные особенности статистического поведения любых макросистем.

Начнем со случая, когда полное число молекул равно четырем (рис.).

Каждая молекула с равной вероятностью может находиться как в левой, так и в правой половине сосуда. Поэтому вероятность того, что, скажем, молекула 1 окажется в левой половине сосуда, равна 1/2. Пребывание в левой половине сосуда молекулы 1 и пребывание в той же половине сосуда молекулы 2 являются статистически независимыми событиями. Поэтому вероятность одновременного нахождения в левой части сосуда молекул 1 и 2 равна произведению вероятностей, т. е. (1/2)2. Продолжая эти рассуждения, получим, что вероятность одновременного нахождения в левой половине сосуда всех четырех молекул равна (1/2)4.

Аналогичные рассуждения дают, что вероятность любого размещения молекул в сосуде (скажем такого, при котором 1-я и 4-я молекулы будут находиться в левой половине сосуда, а 2-я и 3-я — в правой), также равна (1/2)4. Каждое из размещений представляет собой некоторое микросостояние газа. Из сказанного выше следует, что вероятность всех микросостояний одинакова и равна (1/2)4.

Состояние

Способы реализации состояния

Число способов

число молекул слева

число молекул справа

№ молекул, находящихся слева

№ молекул, находящихся справа

реализации данного состояния ( ω )

Всего способов

В табл. 1 приведены все мыслимые способы распределения молекул между половинами сосуда (все микросостояния газа). Состояние, характеризуемое тем, что, скажем, в левой части сосуда находится одна молекула (безразлично какая), а в правой части — три молекулы, представляет собой макросостояние. Из таблицы видно, что такому макросостоянию соответствует 4 микросостояния. Следовательно, статистический вес данного макросостояния равен 4, а вероятность (обычная, а не термодинамическая) равна 4/16. Макросостояние, при котором в обеих частях сосуда находится одинаковое число молекул, реализуется с помощью шести микросостояний. Соответственно его статистический вес равен 6, а вероятность (обычная) равна 6/16.

Из рассмотренного примера вытекает, что все микросостояния данной системы равновероятны, вследствие чего статистический вес оказывается пропорциональным вероятности (обычной) макросостояния. Утверждение о равновероятности всех микросостояний лежит в основе статистической физики и носит название эргодической гипотезы.

Согласно табл. в случае четырех молекул имеется большая вероятность (равная 1/8) того, что все молекулы соберутся в одной из половин сосуда (левой или правой). Однако с увеличением числа молекул положение существенно меняется.

Найдем число способов (число микросостояний), посредством которых может быть осуществлено макросостояние, характеризуемое тем, что в левой половине сосуда окажется n молекул из общего числа их N, а в правой половине — (N — n) молекул. Для этого пронумеруем молекулы, приписав им номера от 1 до N. Затем станем отбирать по одной молекуле и помещать их в левую половину сосуда. Первую молекулу можно выбрать N способами, вторую — (N—1) способом, третью — (N—2) способами, наконец, n-ю молекулу можно выбрать (N— n+1) способом. Оставшиеся (N — n) молекул поместим в правую половину сосуда.

В результате для статистического веса получается выражение

В табл. 2 приведены значения ω , вычисленные по формуле для случая N=24. Полное число способов распределения 24 молекул между двумя половинами сосуда равно 2 24 =16 777 216, и только в двух случаях все молекулы оказываются сосредоточенными в одной из половин сосуда. Вероятность такого события равна примерно 10 ‑7 . В четырех кубических сантиметрах воздуха содержится около 10 20 молекул. Вероятность того, что все эти молекулы соберутся в одной из половин сосуда, равна двум, деленным на два в степени 10 20 , что составляет приблизительно . Эта вероятность настолько мала, что практически ее можно считать равной нулю.

Источник

СТАТИСТИЧЕСКИЙ ВЕС

Понятие «статистический вес» (используется также термин термодинамическая вероятность) является одним из основных в статистической физике. Чтобы сформулировать его определение необходимо сначала определить понятия макросостояние и микросостояние.

Одно и тоже состояние макроскопического тела можно охарактеризовать по-разному. Если состояние охарактеризовано заданием макроскопических параметров состояния (давление, объем, температура, плотность и т.п.) то такое состояние будем называть макросостоянием.

Если состояние охарактеризовано путем задания координат и скоростей всех молекул тела, то такое состояние будем называть микросостоянием.

Очевидно, что одно и то же макросостояние может быть реализовано различными способами, то есть различными микросостояниями. Число различных микросостояниий, которыми может быть реализовано данное макросостояние называется статистическим весом или термодинамической вероятностью.

Для пояснения указанных понятий рассмотрим модель (!) — сосуд, в котором находятся N молекул. Предположим, что сосуд разделен на две одинаковые части, и различные макросостояния отличаются количеством молекул в левой и правой половинах сосуда. Поэтому в рамках модели будем считать состояние молекулы заданным, если известно, в какой из половин сосуда она находится.

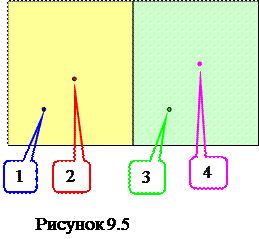
Различные микросостояния отличаются при этом тем, какие именно молекулы находятся справа и слева. 1,2 – 3,4 (как показано на рисунке 9.5) одно из состояний. 1,3 – 2,4 – другое микросостояние.

Каждая из молекул может с равной вероятностью находиться и слева, и справа. Поэтому вероятность i-той молекуле находиться, например, справа равна ½. Появление в левой части сосуда той молекулы наряду с той является статистически независимым событием, поэтому вероятность нахождения слева двух молекул равна ½ ½ = ¼; трех молекул – 1/8; четырех – 1/16 и т.д. Следовательно, вероятность любого размещения (микросостояния) молекул равна .

Читайте также:  Заросли сущ способ образования

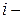
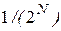
Утверждение о том, что, вероятности каждого их микросостояний равны, называются эргодической гипотезой, и оно лежит в основе статистической физики.

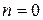
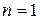
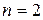
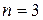
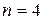
Рассмотрим N = 4. Каждое из размещений молекул в половинах сосуда является конкретным микросостоянием. Тогда макросостоянию с числом молекул слева соответствует 1 микросостояние. Статистический вес такого макросостояния равен 1, а вероятность его реализации – 1/16. Для иных макростоляний можно утверждать следующее:

соответствует 4 микросостояния статистический вес 4, 4/16

соответствует 6 микросостояний статистический вес 6, 6/16

соответствует 4 микросостояния статистический вес 4, 4/16

соответствует 1 микросостояние статистический вес 1, 1/16

Теперь можно видеть, что вследствие принятия эргодической гипотезы, статистический вес оказывается пропорциональным вероятности (обычной!) реализации данного макросостояния.

Если в сосуде содержится N молекул, то можно доказать, что статвес макросостояния, заключающегося в том, что слева n молекул, а справа (N – n)

(9.25)

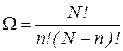
Если для четырех молекул вероятность собраться в одной из половин сосуда составляет 1/16, то есть вполне ощутимую величину, то уже для N = 24 эта вероятность составляет порядка .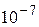

При нормальных условиях в 4 см 3 воздуха содержится около 10 20 молекул. Вероятность собраться им в одной из частей сосуда оценивается величиной .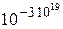

Таким образом, с увеличением количества молекул в системе вероятность существенных отклонений от приблизительного равенства количеств молекул в частях сосуда очень быстро убывает. Это соответствует тому, что статвес состояний с приблизительно равным количеством молекул в половинах оказывается очень большим и быстро убывает по мере отклонения от равенства молекул в частях.

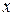
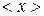
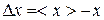
Если число N не очень велико, то с течением времени наблюдаются – заметные отклонения количества молекул в одной из половины от N / 2. Случайные отклонения физической величиныx от ее среднего значения называются флуктуациям:

. (9.26)

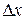
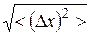
Среднее арифметическое абсолютной флуктуации равно нулю. Поэтому в качестве характеристики флуктуаций чаще рассматривают среднюю квадратичную флуктуацию:

. (9.27)

Более удобной и показательной является относительная флуктуация:

. (9.28)

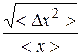
Причем в статистической физике доказывается соотношение:

, (9.28)

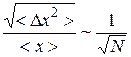
т.е. величина относительной флуктуации обратно пропорционально корню из количества частиц в системе. Это утверждение подтверждает наш качественный вывод.

Аналогично количеству молекул в одной из половин сосуда флуктуируют вблизи средних значений и другие макроскопические характеристики состояния – давление, плотность, и т.п.

Рассмотрим природу равновесных и неравновесных состояний и процессов с точки зрения статистической физики. Равновесным, по определению, является такое состояние, которое не имеет тенденции к изменению с течением времени. Ясно, что таким свойством в наибольшей мере будет обладать наиболее вероятное из всех макросостояний системы, то есть состояние, реализуемое наибольшим количеством микросостояний, а значит обладающее наибольшим статистическим весом. Поэтому равновесное состояние можно определить как состояние, статвес которого максимален.

Примером типичного необратимого процесса может служить распространение на весь объем сосуда молекул газа, первоначально сосредоточенных в одной из его половин. Этот процесс является необратимым, так как вероятность того, что в результате теплового движения все молекулы соберутся в одной из половин сосуда, очень мала. Соответственно всегда необратимым является процесс, обратный которому крайне маловероятен.

ЛЕКЦИЯ № 10 СТАТИЧЕСКАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Читайте также:  Этническое смешивание как способ мирного сотрудничества одно предложение

Как мы установили, вероятность состояния системы пропорциональна ее статическому весу, поэтому в качестве характеристики вероятности состояния можно было бы использовать сам статвес W. Однако W не является аддитивной величиной. Поэтому для характеристики состояния системы используют величину

(1)

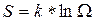
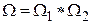
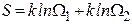
которую называют энтропией системы. Действительно, если мы рассмотрим две системы по 4 молекулы в каждой, то статистический вес состояния, когда в каждой из подсистем находится, например, по одной молекуле слева будет равен 16, т.е. . Это соотношение справедливо для любых состояний. Следовательно, статвес неаддитивен. В то же время энтропия состояния результирующей системы т.е. является величиной аддитивной.

Поскольку при протекании необратимых процессов в изолированной системе она переходит из менее вероятных в более вероятные состояния, можно утверждать, что энтропия изолированной системы возрастает при протекании в ней необратимых процессов.

Равновесное состояние является наиболее вероятным состоянием, а значит, энтропия системы перешедшей в равновесное состояние максимальна.

Поэтому можно утверждать, что энтропия изолированной системы остается постоянной, если она находится в равновесном состоянии, или возрастает, если в ней протекают необратимые процессы.

Утверждение о том, что энтропия изолированной системы не убывает, называетсявторым началом термодинамики или законом возрастания энтропии.

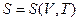
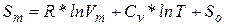
Энтропия является, очевидно, функциейсостояния и должна определятся параметрами состояния. Самыми простыми свойствами обладает одноатомный идеальный газ – его состояния полностью определяется заданием двух параметров, например, температуры и объема. Соответственно его энтропию можно определить как функцию температуры и объема: . Соответствующие вычисления показывают, что энтропия моля идеального газа определяется выражением

(2)

где 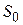— есть некоторая константа, с точностью до которой определяется энтропия.

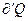
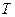
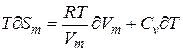
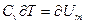
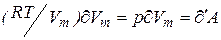
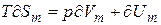
Теперь можно выяснить вопрос о том, как изменяется энтропия неизолированной системы, например при сообщении ей некоторого количества тепла . Возьмем дифференциал (2) и умножим его на :

(3)

Но приращению внутренней энергии газа. Поскольку равенство .Тогда (3) преобразуется к виду:

(4)

Входящие в (4) 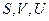являются аддитивными, и поэтому (4) справедливо для любой массы газа:

(5)

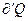
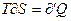
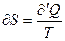
Согласно первому началу термодинамики правая часть(5) есть . По этому:

и (6)

Формула(6) оказывается справедливой для любых тел, необходимо только чтобы сообщение количества тепла 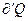было обратимым.

Остановимся на физической сущности энтропии.

Введем определения: состояние, осуществляемое относительно малым числом способов будет называться упорядоченным или неслучайным. Состояние, осуществляемое большим количеством способов – беспорядочным или случайным.

Тогда можно утверждать, что энтропия является количественной мерой степени беспорядка в системе. Сообщение системе количества тепла приводит к усилению теплового движения молекул, а значит и к росту энтропии. При этом, чем выше температура системы, тем меньше доля беспорядка вносимого сообщением данного 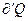, в чем и заключается физический смысл формулы(6).

Если количество тепла сообщается системе в ходе необратимого процесса, то ее энтропия возрастает не только за счет получения тепла, но и за счет протекания необходимых процессов, поскольку необратимый процесс сопровождается ростом вероятности состояния системы, ее статистического веса

(7)

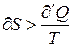
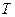
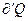
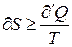
В этом случае под в(7) подразумевается температура резервуара, из которого система получает . Объединяя (6) и(7) вместе можно записать:

(8)

При абсолютном нуле всякая система находится в основном состоянии, т. е. состоянии с наименьшей энергией. Статический вес этого вполне определенного состояния равен единице, а значит энтропия системы равна нулю. Это соответствует теореме Нернста, согласно которой энтропия всякого тела стремится к нулю при стремлении к нулю его температуры:

Теорему Нернста называют также третьим началом термодинамики.

Источник