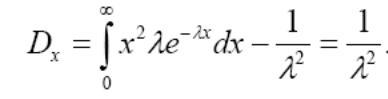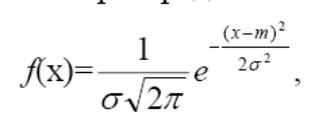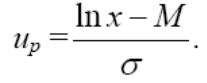Статистический способ оценки закона распределения

4. Статистическая оценка законов распределения в задачах надежности

Распределение Пуассона (однопараметрическое с параметром λ) закономерность появления случ. отказов в сложных системах. Применение при опр-ии Р появления и восстановления отказов. Случайная величина Х распределена по З. Пуассона, если Р, выражается P_m= λ m e -λ /m! ,где λ-параметр распределения (некоторая положит. величина); m=0, 1. 2, Мат ожидание и дисперсия случайной величины х для З Пуассона= пар-ру распр-ия λ:M_x.=D_x= λ Экспоненциальный закон распр-ия осн. закон надежности, для прогнозирования надеж-ти в период норм эксплуатации изделий, постепенные отказы еще не проявились и надежность хар-ся внезапными отказами. имеющими пост интенсивность Плотность распр-ия эксп закона: f (x) = λe −λx ;

фу-ция распределения: F(x) = 1− e −λx

фу-ция надежности: P(x) = 1− F(x) = e −λx ;

мат ожидание величины Х: дисперсия

Норм.закон распр-ия закон Гаусса. — предельный закон, к нему приближаются др. законы распр-ия. Для описания постеп/ отказов, распр-ие времени безотказной работы в начале имеет низкую плотность, затем макс. далее плотность снижается. Расп-ие подчиняется норм. закону, если на изменение случ величины оказывают влияние многие,≈равнозначные факторы. Норм закон распр-ия описывается плотностью вероятности

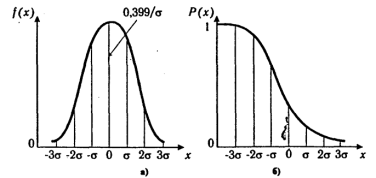
где е = 2,71828 — основание натурального логарифма; π= 3,14159; т и σ –пар-ры распр-ия, по рез-там испытаний. Колоколообразная кривая приведена на рис.

Логарифмически норм. Распр-ие для описания наработки до отказа подшипников, электронных ламп Неотрицательная случ величина распределена лог-и норм, если ее lg распределен норм. Плотность распределения для различных значений σ приведена на рис. Р безотказной работы можно опр-ть по табл для норм распр-ия в зависимости от значения квантили

Распределение Вейбулла двухпараметр распр-ие. универсальное, т.к. при соответ. значениях пар-ров мб норм, экспоненц. и др. З. Вейбулла описывает наработку до отказа подшипников, Эл-ов радиоэл. аппаратуры, Плотность распределения где α — пар-р формы кривой распределения; λ — пар-р масштаба; Для изделий, со скрытыми дефектами, но длительное время не стареют, α 1. При α =3.3 распр-ие Вейбулла близко к норм. Гамма-распределение – двухпараметр-ое распр Плотность распр-ия (0 ≤ х ≤ ∞). Применяют при описании появления отказов стареющих элементов, времени восстановления, наработки на отказ резервир. систем. При различ. Пар-рах г.распр-ие принимает разнообразные формы, Плотность вероятности гамма-распр-ия определяется равенствами ,при х≥0

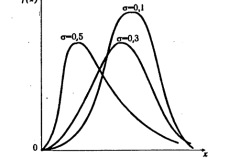
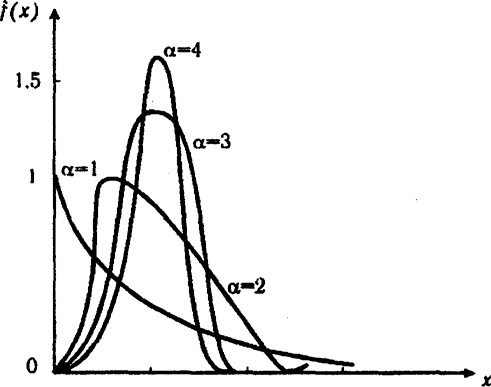
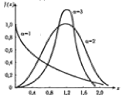
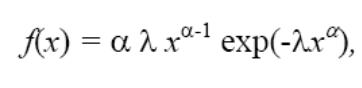
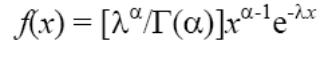
f(х)=0, при х=0 где

Гистограмма, наим квадраты

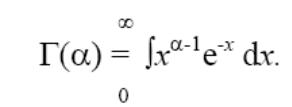
5.Вероятностаня оценка отказа в работе технического объекта

Все пар-ры используемые в над-ти вероятностные и с допущениями.

Вероятностная оценка дерева отказов

Схема ИЛИ. с двумя входами, изображенную на рис.1 Для этой схемы вероятность появления завершающего события имеет вид

Р(Т) = Р(a) + Р(b) — Р(а *b). (8.5)

В случае схемы ИЛИ с n входами имеем

Р(а + b + с + . ) ≈ Р(а) + Р(b) + Р(с)+ . .

Схема И. В случае схемы И с двумя входами (рис. 8.15) события а и b статистически независимы и для получения вероятности появления завершающего события применяется правило умножения вероятностей: Р(аb) = Р(а) *Р(b).Для схемы И с n входами данное выражение можно записать в общем виде:

Р(а . b . с . ) = Р(а) *Р(b)*Р(с) . (8.8)

Пример 8.8. Требуется вычислить вероятность появления завершающего события дерева неисправностей, изображенного на рис.3

Допустим, что основные события А, В, C, D и Е статистически независимы и что Р(А)= Р(В) = Р(С) = Р(D) = Р(Е) = 1/4. В данном случае дерево не содержит повторяющихся элементарных событий, поэтому можно вычислить вероятность конкретных событий на выходе каждой логической схемы. Однако если бы в ветвях дерева неисправностей присутствовали повторяющиеся события, то сначала необходимо было бы исключить повторяющиеся событий.

Для данного дерева неисправностей решение может быть получено следующими двумя методами. Метод 1. Запишем выражение для завершающего события через элементарные со-

бытия т. е.Т0 = Т1 + Т2. (8.9)

Поскольку T2 = CD, T1 = T3E, Т3 = А + В, то To = E(A + B) + CD, и, следовательно,

Р(Т0) = Р(ЕА + EB + CD). (8.10)

Раскрывая полученное выражение, можно получить формулу для вероятности появления завершающего события. При допущении о статистической независимости событий (отказов) можно найти колич оценку вероятности появления завершающего события.

Метод 2. Этот метод определения численного значения вероятности появления завершающего события основан на вычислении вероятностей появления промежуточных событий. В данном случае предполагается, что события (отказы) статистически независимы.

Используя правило умножения вероятностей, получаем следующие количественные рез-ты для вероятностей появления промежуточных событий и завершающего события:

Р(Т3) = Р(А) + Р(В) — Р(А).Р(В) = 1/4 + 1/4 — 1/16 = 7/16,

Р(Т2) = P(С).Р(D) = 1/4 . 1/4 = 1/16,

Р(Т1) = Р(Т3).Р(Е) = 7/16 . 1/4 = 7/64,

Р(Т0) = Р(Т1) + Р(Т2) — Р(Т1).Р(Т2)= 7/64 + 1/16 — 7/64 . 1/16 = 169/1024

Источник

Статистический способ оценки закона распределения

ГОСТ Р 50779.21-2004

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

ПРАВИЛА ОПРЕДЕЛЕНИЯ И МЕТОДЫ РАСЧЕТА
СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ПО ВЫБОРОЧНЫМ ДАННЫМ

Statistical methods. Determination rules and methods
for calculation of statistical characteristics based on sample data.
Part 1. Normal distribution

Дата введения 2004-06-01

1 РАЗРАБОТАН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции»

2 ВНЕСЕН Научно-техническим управлением Госстандарта России

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 12 января 2004 г. N 3-ст

4 Настоящий стандарт разработан с учетом основных нормативных положений международного стандарта ИСО 2854:1976 «Статистическое представление данных. Методы оценки и проверки гипотез о средних значениях и дисперсиях» (ISO 2854:76 «Statistical interpretation of data — Techniques of estimation and tests relating to means and variance», NEQ)

Информация об изменениях к настоящему стандарту публикуется в указателе «Национальные стандарты», а текст этих изменений — в информационных указателях «Национальные стандарты». В случае пересмотра или отмены настоящего стандарта соответствующая информация будет опубликована в информационном указателе «Национальные стандарты»

Введение

Стандарт устанавливает процедуры и методы решения ряда практических задач статистики в случае, когда наблюдаемые величины являются случайными и распределены по нормальному закону.

В стандарте изложены методы решения следующих задач:

а) точечного оценивания параметров нормального распределения случайной величины;

б) точечного оценивания вероятности попадания (доли распределения) случайной величины в заданный интервал и вне его;

в) интервального (доверительного) оценивания параметров нормального распределения и доли распределения;

г) проверки гипотез об этих же величинах.

Все процедуры, приведенные в стандарте, используют ограниченный ряд статистически независимых наблюдений, полученных в производстве, в лабораторных условиях, при контроле, измерении, оценке и т.п.

1 Область применения

Настоящий стандарт устанавливает методы, применяемые для:

— оценки математического ожидания и дисперсии генеральной совокупности;

— проверки гипотез относительно значений этих параметров;

— оценки вероятности попадания (доли распределения) случайной величины в заданный интервал.

Примечание — Вероятность попадания случайной величины в интервал равна доле распределения случайной величины в этом интервале. В большинстве практических задач физический смысл имеет понятие «доля распределения случайной величины в интервале», которое далее применено в настоящем стандарте.

Методы, изложенные в настоящем стандарте, применимы в том случае, если выполнены следующие условия:

— элементы выборки получены путем независимых повторений эксперимента. В случае конечной генеральной совокупности объем выборки должен составлять не более 10% объема генеральной совокупности;

— наблюдаемые переменные распределены по нормальному закону. Однако если распределение вероятностей несильно отличается от нормального, то описанные в стандарте методы остаются применимыми для большинства практических приложений. В этом случае объем выборки должен быть не менее 10 единиц, причем достоверность получаемых статистических выводов возрастает при увеличении объемов выборок.

2 Нормативные ссылки

В настоящем стандарте использованы ссылки на следующие стандарты:

Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов по указателю «Национальные стандарты», составленному по состоянию на 1 января текущего года, и по соответствующим информационным указателям, опубликованным в текущем году. Если ссылочный документ заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться замененным (измененным) стандартом. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены термины по ГОСТ Р 50779.10 и ГОСТ Р 50779.11, а также следующие термины с соответствующими определениями:

3.1 точечное оценивание параметра: Получение оценки параметра в виде одного численного значения;

3.2 интервальное (доверительное) оценивание параметра: Получение оценки параметра в виде доверительного интервала;

3.3 доверительный интервал: Интервал, границы которого являются функциями от выборочных данных и который накрывает истинное значение оцениваемого параметра с вероятностью не менее 1- (где 1- — доверительная вероятность).

Примечание — Доверительный интервал может быть двусторонним или односторонним;

3.4 нулевая гипотеза: Предположение о распределении генеральной совокупности, которое проверяют по статистическим данным.

Примечание — В частности, в настоящем стандарте рассмотрены предположения о значениях параметров распределения.

4 Обозначения

В настоящем стандарте применены следующие обозначения:

математическое ожидание нормального закона распределения (среднее значение генеральной совокупности, далее — среднее значение);

известное значение параметра ;

математические ожидания для двух различных генеральных совокупностей;

точечная оценка параметра ; ;

верхняя и нижняя доверительные границы параметра ;

—

точечная оценка разности значений параметров и ;

стандартное (среднеквадратичное) отклонение нормально распределенной случайной величины;

дисперсия генеральной совокупности; ;

известное значение дисперсии генеральной совокупности, ;

известное численное значение параметра ;

известные значения параметров и для двух генеральных совокупностей;

точечная оценка параметра , ;

верхняя и нижняя доверительные границы параметра ;

точечная оценка дисперсии;

выборочное значение наблюдаемой случайной величины;

выборочное значение случайной величины из первой генеральной совокупности;

то же, из второй генеральной совокупности;

среднеарифметические значения (выборочные средние);

—

выборочное стандартное (среднеквадратичное) отклонение;

то же для двух выборок соответственно;

риск первого рода (вероятность отвергнуть гипотезу, когда она верна);

—

уровень значимости при проверке гипотез, а также доверительная вероятность ;

число степеней свободы;

, —

квантили стандартного нормального закона распределения уровней и соответственно;

, —

квантили распределения Стьюдента с степенями свободы уровней и соответственно;

—

квантиль распределения Фишера с и степенями свободы уровня ;

, , —

квантили распределения с степенями свободы уровней , и соответственно;

нижняя и верхняя границы интервала соответственно;

доля распределения (вероятность попадания) случайной величины в заданный интервал ;

доля распределения (вероятность попадания) случайной величины вне интервала , причем ;

точечные оценки и ;

нижние односторонние доверительные границы для и ;

верхние односторонние доверительные границы для и ;

случайное событие: например, попадание случайной величины в заданный интервал;

—

вероятность случайного события ;

сумма выборочных значений.

5 Общие требования

5.1 Настоящий стандарт содержит описание типовых статистических задач, а также процедур, при помощи которых они решаются. Представленные задачи могут быть разбиты на три класса:

— точечное и интервальное оценивание среднего значения генеральной совокупности;

— точечное и интервальное оценивание дисперсии генеральной совокупности;

— точечное и интервальное оценивание доли распределения (вероятность попадания) случайной величины в заданном интервале и вне его.

5.2 Для решения каждой из перечисленных задач по 5.1 приведены процедуры их решения (разделы 6, 7, 8), включающие в себя:

Источник