Статический способ построения линий влияния

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Линии влияния

Линией влияния в балке называется график, показывающий изменение исследуемого фактора (опорной реакции, поперечной силы, изгибающего момента и т.д.) при движении по балке единичной силы.

Любая ордината линии влияния показывает величину исследуемого фактора в тот момент, когда сила находится над этой ординатой.

Статический способ построения линий влияния в балках основан на составлении уравнений статики (уравнений равновесия). Рассмотрим простую балку на двух шарнирных опорах. По балке движется сила, равная 1. Мысленно зафиксируем силу на расстоянии z от опоры А.

1. Построение линии влияния реакции R_A. Составим уравнение моментов вокруг опоры В.

Получаем аналитическое выражение для реакции R_A.

Строим график по 2м точкам.

2. Аналогично строится линия влияния реакции R_B. Составим уравнение моментов вокруг опоры А.

Получаем аналитическое выражение для реакции R_В. Строим график по 2м точкам:

3. Построим линию влияния поперечной силы Q_K .

Возьмем произвольное сечение k, находящееся на расстоянии a от опоры A. Рассмотрим два положения силы — слева и справа от сечения.

a) сила находится слева от сечения K, находящееся на расстоянии a от опоры A, а рассматривать будем правую часть.Тогда

Это значит, что линия влияния Q_K такая же, как линия влияния R_B, но с отрицательным знаком. Строим данную линию влияния, но обводим лишь левую ее часть, так как она справедлива, когда сила слева от сечения. Значит, мы получаем левую ветвь линии влияния.

b) сила справа от сечения K, а рассматривать будем левую часть, тогда . Это значит, что линия влияния Q_K такая же, как линия влияния R_А. Строим данную линию влияния, но обводим лишь правую ее часть, так как она справедлива, когда сила справа от сечения. Значит, мы получаем правую ветвь линии влияния.

При построении линии влияния поперечной силы для простой балки следует запомнить величины ординат линии влияния в сечении, а именно и .

4. Построим линию влияния изгибающего момента М_K

a) сила находится слева от сечения K, а рассматривать будем правую часть, тогда . Это значит, что линия влияния М_K такая же, как линия влияния R_B, но в b раз больше. Строим данную линию влияния, но обводим лишь левую ее часть, так как она справедлива, когда сила слева от сечения. Значит, мы получаем левую ветвь линии влияния.

b) сила справа от сечения K, а рассматривать будем левую часть, тогда . Это значит, что линия влияния М_K такая же, как линия влияния R_А, но в а раз больше. Строим данную линию влияния, но обводим лишь правую ее часть, так как она справедлива, когда сила справа от сечения. Значит, мы получаем правую ветвь линии влияния.

При построении линии влияния моментов для простой балки следует запомнить величину наибольшей ординаты линии влияния, а именно .

Кинематический способ построения линий влияния основан на принципе возможных перемещений.

1) Для того чтобы построить линию влияния реакции какой-нибудь опоры нужно изобразить балку без этой опоры, дать данной точке возможное перемещение в положительном направлении (вверх на единицу), и зарисовать новое положение полученного механизма.

2) Для того чтобы построить линию влияния изгибающего момента M_K , нужно в данное сечение врезать шарнир и повернуть полученный механизм в положительном направлении на единичный угол.

3) Для того чтобы построить линию влияния поперечной силы Q_K, нужно в данное сечение врезать ползун и раздвинуть части балки в положительном направлении на единицу.

Построим линии влияния кинематическим методом в этой же балке. Линии влияния получились такие же.

Построим линии влияния поперечной силы и изгибающего момента в консольной балке кинематическим способом. Так как левая часть в этой балке неподвижна, то движется только правая часть в положительном направлении. При этом ордината линии влияния момента равна а, ордината линии влияния поперечной силы равна 1.

С помощью линий влияния можно определить любые усилия по формуле:

где сила считается положительной, если направлена вниз

— это ордината линии влияния под силой, берется со своим знаком,

q — нагрузка считается положительной, если направлена вниз

— это площадь в линии влияния под нагрузкой, берется со своим знаком,

М — момент считается положительным, если направлен по часовой стрелке

— это тангенс угла наклона линии влияния над моментом, равный и считается положительным, если линия влияния возрастает.

Источник

2.1. Методы построения линий влияния

Линии влияния усилий в заданном сечении сооружения строят двумя методами: статическим и кинематическим.

2.1.1. Статический метод построения линий влияния

Груз F=1 устанавливается в произвольном сечении, положение которого фиксируется переменной X (рис. 10). Из условия равновесия системы записывается аналитическое выражение определяемого усилия J=f(x). Подставляя в него значение координат, фиксирующих положение груза F=1, вычисляют ординаты лв, расположенные под нагрузкой, и строят график.

Рис. 1.10. Линии влияния усилий

При построении линий влияния усилий М_к, Q_к для фиксированного сечения “К”, расположенного между опорами, следует рассматривать два положения груза F=1 – слева и справа от сечения “К”, при этом рассматривая равновесие соответственно правой и левой отсечённых частей. В данном случае запись уравнений М_к, Q_к проще. В том случае, когда сечение расположено на консоли, при движении груза F=1 слева и справа от сечения целесообразно рассматривать равновесие консольной части, считая, что груз движется от сечения.

За пределами сооружения линии влияния нулевые.

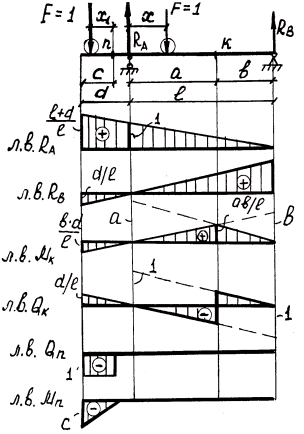
Линии влияния усилий RA, RB, MK, QK, Mn, Qn показаны на рис.2.1.

Линии влияния RA

Из уравнения статики определяем реакцию RA.

уравнение прямой, для построения которой достаточно двух точек.

Груз F=1 находится на консоли, х = -d,

По полученным значениям строим линию влияния опорной реакции R_A.

Линия влияния RB

,

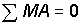
Линия влияния R_b(x) изменяется по линейному закону. Подставляем координаты Х в уравнение лв Rb:

Характеристики линии влияния реакции R:

состоит из одной ветви;

над опорой, для которой определяется усилие R, отсекает ординату равную плюс 1;

на противоположной опоре ордината равна нулю.

Линия влияния изгибающего момента М_К.

Сечение “К” расположено между опорами: . ГрузF = 1 слева от сечения К, рассматривается равновесие правой части балки.

Линия влияния, построенная в предположении, что груз F = 1 перемещается слева от сечения К, называется левой ветвью линии влияния. Левая ветвь лв М_К представляет лв R_B, увеличенную в b раз.

Груз F=1 справа от сечения К, равновесие левой части, .

Характеристики линии влияния М_К, сечение “К” расположено между опорами:

состоит из двух ветвей: левая ветвь справедлива от левой опоры до сечения, правая ветвь – от правой опоры до сечения;

ветви всегда пересекаются под сечением;

ветви отсекают над опорой расстояние от данной опоры до сечения.

Линия влияния поперечной силы Q_K

Сечение К расположено между опорами: . Груз F=1 слева от сечения, равновесие правой части.

; лв мQ = -ЛВ RB;

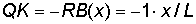
Груз F=1 справа от сечения К, равновесие левой части .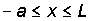

Характеристики лв Q_K, сечение между опорами:

– состоит из двух параллельных ветвей;

– правая ветвь отсекает над левой опорой ординату равную плюс 1, а левая ветвь под правой опорой отсекает ординату равную минус 1;

– в сечении наблюдается скачок равный 1.

Линия влияния Mn

Сечение n расположено на консоли, .

Груз F = 1 слева от сечения n, равновесие консольной (левой) части балки.

Груз F = 1 справа от сечения n, равновесие консольной (левой) части балки.

Mn = 0 — правая ветвь.

Правая ветвь со стороны опор – нулевая, поскольку рассматривается равновесие той части балки, на которой нагрузка отсутствует. Следовательно, ветвь со стороны опор совпадает с осью линии влияния.

Характеристики ЛВ Мn, сечение на консоли:

состоит из двух ветвей;

ветви всегда пересекаются под сечением;

ветвь со стороны опор, заделки всегда нулевая;

ветвь со стороны консоли отсекает на конце консоли ординату, равную расстоянию от сечения до конца консоли.

Линия влияния Qn

Груз F =1 слева от сечения n, равновесие консольной части.

Груз F =1 справа от сечения n, равновесие консольной части.

Qn(x1) = 0 — правая, нулевая ветвь.

Характеристики ЛВ Qn, сечение на консоли:

состоит из двух параллельных ветвей;

ветвь со стороны опор всегда нулевая;

ветвь на консольной части параллельна оси линии влияния и отсекает в сечении ординату равную минус 1, если консоль расположена слева от опор, и плюс 1 – если консоль справа от опор;

в сечении – скачок равный единице.

2.1.2. Кинематический метод построения линий влияния

Кинематический метод основан на принципе возможных перемещений: если система находится в равновесии, то сумма работ всех сил, действующих на систему, на любых возможных бесконечно малых перемещениях равна нулю.

Суть кинематического метода построения линий влияния заключается в следующем:

отбрасывается связь, усилие в которой определяется, получается механизм с одной степенью свободы;

вместо отброшенной связи прикладывается искомое усилие;

по направлению искомого усилия системе даётся единичное перемещение и строится эпюра перемещений полученного механизма. Построенная эпюра перемещений даёт вид линии влияния;

для получения ординат линии влияния записывается уравнение работ при определённом положении груза F = 1;

характерные ординаты линии влияния определяются из геометрических построений.

Вид эпюр перемещений в соответствии с рис. 2.2 получают для построения линий влияния:

опорной реакции R – отбрасыванием опорного стержня, действие которого заменяется силой R;

изгибающего момента М – в каком-либо сечении врезанием шарнира в заданное сечение, действие нарушенной связи компенсируется приложением двух равных и противоположно направленных моментов;

поперечной силы Q – в каком-либо сечении введением в заданное сечение ползуна, при этом, стержни системы всегда остаются параллельными. Замена нарушенной связи осуществляется приложением к концам получившихся частей бруса двух равных и противоположно направленных сосредоточенных сил.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник