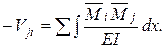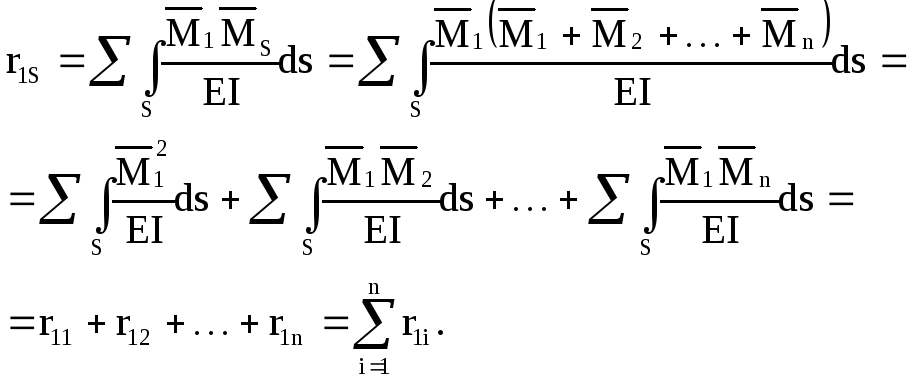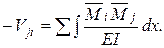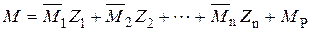- Определение коэффициентов канонических уравнений. Коэффициенты канонических уравнений метода перемещений можно определять статическим или кинематическим способами.
- 4.5 Методы вычисления коэффициентов и свободных членов канонических уравнений
- 4.6 Проверки метода перемещений
- Определение коэффициентов канонических уравнений. Коэффициенты канонических уравнений метода перемещений можно определять статическим или кинематическим способами.
Определение коэффициентов канонических уравнений. Коэффициенты канонических уравнений метода перемещений можно определять статическим или кинематическим способами.
Коэффициенты канонических уравнений метода перемещений можно определять статическим или кинематическим способами.
Статический способ основан на определении реакций во введенных связях основной системы из уравнений статики. Для этого необходимо вырезать отдельные узлы или части основной системы и составлять уравнения равновесия (статики). Если искомая реакция является реактивным моментом, то она определяется из условия равенства нулю момента в узле SM=0, если же она является реактивной силой, то определяется из уравнения проекции на ось (например, на ось x) в направлении этой реакции SX=0. Статический способ достаточно прост для использования, поэтому является основным способом определения коэффициентов системы канонических уравнений.
Докажем одну полезную теорему.
Теорема Релея. Реакция, возникающая в j-ой связи от перемещения i-ой связи на единицу, равна реакции i-ой связи от перемещения j-ой связи на единицу, т.е.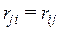 
.
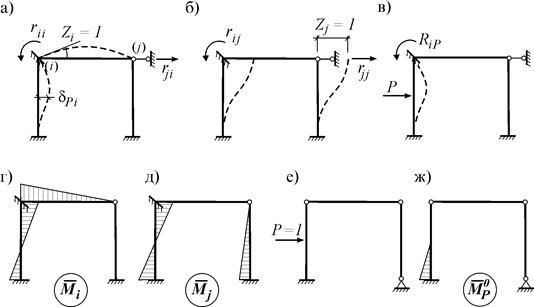
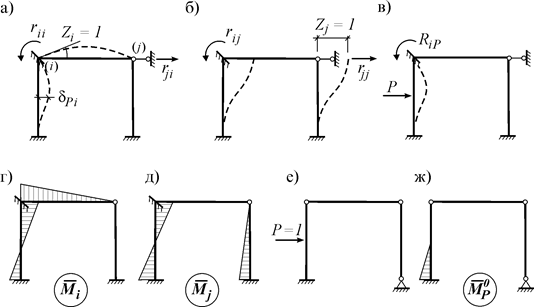
Доказательство. Рассмотрим i-ое и j-ое единичные состояния основной системы некоторой рамы (рис. 11.3 а, б) и соответствующие эпюры моментов в этих состояниях (рис. 11.3 г, д).
Возможная работа сил j-ого единичного состояния (рис. 11.3 б) на перемещениях i-го состояния (рис. 11.3 а) равна
.
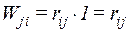
Работа сил i-го состояния на перемещениях j-го состояния будет
.
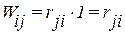
По теореме Бетти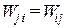 
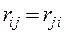
. Значит, равны и правые части, т.е. 
.
Эту теорему иногда называют теоремой о взаимности реакций. Она позволяет сократить объем вычислений побочных коэффициентов канонических уравнений.
Кинематический способ основан на определении коэффициентов канонических уравнений перемножением эпюр. Этот способ применяется при сложности определения коэффициентов статическим способом или для проверки результатов статического способа.
Для вывода формулы кинематического способа определим две возможные работы. Работа внешних сил j-го единичного состояния на перемещениях i-го состояния нам известна: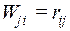 
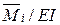
. А возможная работа внутренних сил j-го единичного состояния на деформации i-го состояния 
равна:
По принципу возможных перемещений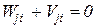 
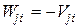
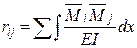
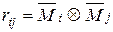
или 
. Отсюда получаем искомую формулу:
или 
.
Формула вычисления грузовых коэффициентов отличается от аналогичной формулы метода сил (дается без вывода):
или 
,
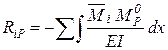
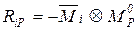
где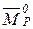 
– грузовая эпюра изгибающих моментов в любой статически определимой системе, полученной из заданной системы удалением лишних связей.
Дата добавления: 2015-06-17 ; просмотров: 1179 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
4.5 Методы вычисления коэффициентов и свободных членов канонических уравнений
В методе перемещений для вычисления коэффициентов и свободных членов канонических уравнений используются два способа: статический и способ интегрирования эпюр.
При статическом способе реактивные усилия во введенных связях определяют из уравнений равновесия отдельных узлов рамы или ее отсеченной части.
Коэффициенты и свободные члены, представляющие собой реактивные моменты во введенных заделках, определяются вырезанием узлов и составлением уравнений вида:
(4.8)
Коэффициенты и свободные члены, представляющие собой реактивные усилия во введенных стержнях, определяются с помощью разреза элементов рамы и составления уравнений равновесия сил, действующих на отсеченную часть:
(4.9)
причем, направление оси L выбирается так, чтобы уравнение получилось наиболее простым. Вычисленное реактивное усилие считается положительным, если его направление совпадает с направлением (соответственно, угловым или линейным) перемещения связи.
Способ интегрирования эпюрцелесообразно применять при расчете рам с наклонными элементами. По этому способу коэффициенты при неизвестных определяют путем интегрирования (перемножения по правилу Верещагина) соответствующих единичных эпюр:
(4.10)
Свободные члены канонических уравнений вычисляются в виде:
(4.11)
где 
— эпюра моментов от нагрузки, построенная в любой статически определимой системе, образованной из заданной.
4.6 Проверки метода перемещений
Так же как и в методе сил, в методе перемещений можно выполнять статическую и кинематическую проверки. Но поскольку основная система метода перемещений кинематически определима, то кинематическая проверка является вспомогательной и выполняется всегда при правильных эпюрах изгибающих моментов в основной системе и при выполненной статической проверке.
Основной проверкойв методе перемещений является проверка равновесия узлов и других частей рамы. Количество проверяемых условий равновесия должно быть не меньше числа неизвестных метода перемещений.
Проверка правильности вычисления коэффициентов при неизвестных системы канонических уравнений метода перемещений выполняется аналогично проверке коэффициентов уравнений при расчете статически неопределимых систем методом сил. Для этого строится суммарная единичная эпюра моментов 
.
Умножая эту эпюру последовательно на каждую из единичных эпюр, получим сумму коэффициентов при неизвестных в соответствующем уравнении; так, умножая эпюру 
на эпюру
, получим:
Аналогично, 
и т.д.
Сумма коэффициентов при неизвестных i-го уравнения должна равняться значению ris, где
(4.12)
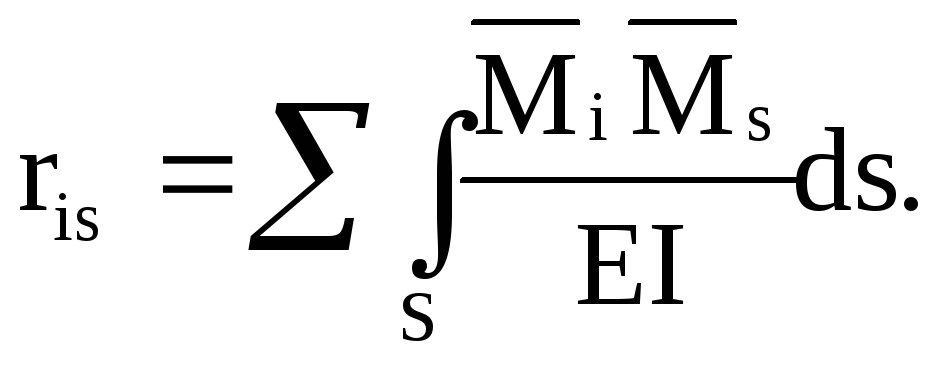
Таким образом, проверка вычисленных значений коэффициентов, входящих в первое каноническое уравнение метода перемещений, состоит в проверке условия:
(4.13)
Аналогично проверяются и коэффициенты всех остальных уравнений. Как и в методе сил, такая проверка называется построчной.
Чаще используется универсальная проверка,которая состоит в том, что результат умножения эпюры
на саму себя должен равняться сумме всех коэффициентов при неизвестных системы канонических уравнений. Действительно,
(4.14)
Для проверки свободных членов канонических уравнений необходимо суммарную единичную эпюру моментов 
умножить на эпюру
, построенную от внешней нагрузки в статически определимой системе, полученной из заданной системы или основной системы метода перемещений устранением лишних связей, в том числе обязательно тех связей, реакции в которых определяются:
(4.15)
Результат перемножения (4.15) должен равняться сумме всех свободных членов канонических уравнений:
(4.16)
Достаточной проверкой правильности окончательной эпюры моментов являются, как уже отмечалось, статические проверки, суть которых будет подробно рассмотрена ниже на конкретных примерах.
Можно также выполнить дополнительную кинематическую проверку подобно тому, как это делается в методе сил. Для этого необходимо построить единичные эпюры в основной системе метода сил и перемножить их или суммарную единичную эпюру с окончательной эпюрой изгибающих моментов. При правильном расчете результат такого перемножения должен быть равен нулю. Эта проверка служит контролем правильности принятых для расчета единичных эпюр и грузовой эпюры изгибающих моментов.
Источник
Определение коэффициентов канонических уравнений. Коэффициенты канонических уравнений метода перемещений можно определять статическим или кинематическим способами.
Коэффициенты канонических уравнений метода перемещений можно определять статическим или кинематическим способами.
Статический способ основан на определении реакций во введенных связях основной системы из уравнений статики. Для этого необходимо вырезать отдельные узлы или части основной системы и составлять уравнения равновесия (статики). Если искомая реакция является реактивным моментом, то она определяется из условия равенства нулю момента в узле SM=0, если же она является реактивной силой, то определяется из уравнения проекции на ось (например, на ось x) в направлении этой реакции SX=0. Статический способ достаточно прост для использования, поэтому является основным способом определения коэффициентов системы канонических уравнений.
Докажем одну полезную теорему.
Теорема Релея. Реакция, возникающая в j-ой связи от перемещения i-ой связи на единицу, равна реакции i-ой связи от перемещения j-ой связи на единицу, т.е.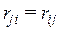 
.
Доказательство. Рассмотрим i-ое и j-ое единичные состояния основной системы некоторой рамы (рис. 11.3 а, б) и соответствующие эпюры моментов в этих состояниях (рис. 11.3 г, д).
Возможная работа сил j-ого единичного состояния (рис. 11.3 б) на перемещениях i-го состояния (рис. 11.3 а) равна
.
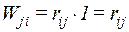
Работа сил i-го состояния на перемещениях j-го состояния будет
.
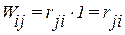
По теореме Бетти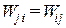 
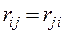
. Значит, равны и правые части, т.е. 
.
Эту теорему иногда называют теоремой о взаимности реакций. Она позволяет сократить объем вычислений побочных коэффициентов канонических уравнений.
Кинематический способ основан на определении коэффициентов канонических уравнений перемножением эпюр. Этот способ применяется при сложности определения коэффициентов статическим способом или для проверки результатов статического способа.
Для вывода формулы кинематического способа определим две возможные работы. Работа внешних сил j-го единичного состояния на перемещениях i-го состояния нам известна: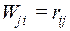 
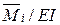
. А возможная работа внутренних сил j-го единичного состояния на деформации i-го состояния 
равна:
По принципу возможных перемещений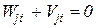 
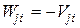
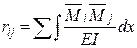
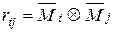
или 
. Отсюда получаем искомую формулу:
или 
.
Формула вычисления грузовых коэффициентов отличается от аналогичной формулы метода сил (дается без вывода):
или 
,
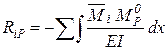
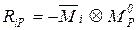
где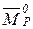 
– грузовая эпюра изгибающих моментов в любой статически определимой системе, полученной из заданной системы удалением лишних связей.
Определение усилий
После определения всех коэффициентов они подставляются в систему канонических уравнений. Затем она решается и определяются неизвестные Z1, Z2, …, Zn. После этого определяются внутренние усилия заданной статически неопределимой системы. Это выполняется аналогично методу сил. Вначале по формуле
определяются моменты. Затем по эпюре M определяются поперечные силы Q, а по ним – продольные силы N.
Источник
