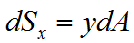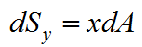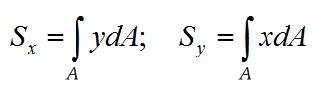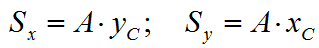Статический момент площади плоской фигуры относительно оси способ вычисления

iSopromat.ru

Формулы для расчета геометрической характеристики статического момента сечений, плоских фигур и площади:

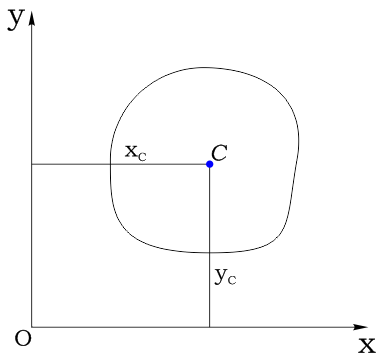
Рассмотрим сечение (плоскую фигуру) произвольной формы площадью A:

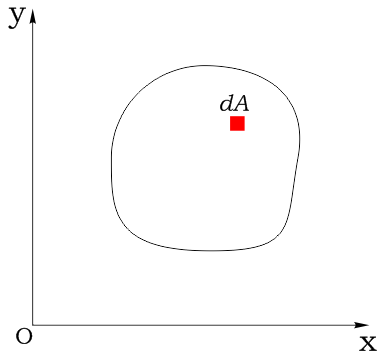
Выделим в нем элементарную площадку dA и зададим систему координат:

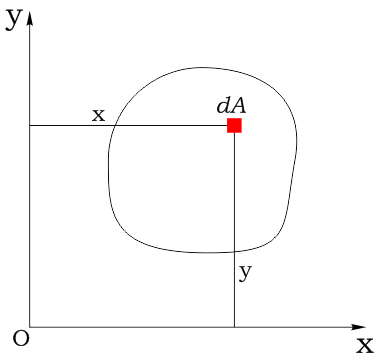
Координаты площадки обозначим соответственно как x и y:

Статический момент элементарной площадки:

• относительно оси x
  
• относительно оси y
  

Суммируя выражения по всей площади фигуры, получим соответственно:

Единица измерения статического момента [м 3 ].

тогда статические моменты относительно осей x и y:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

Набор студента для учёбы

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Источник

Статический момент площади плоской фигуры относительно оси

Статический момент площади плоской фигуры относительно оси

• Формула, стоящая в числителе формулы (7.7), называется статическим моментом в области фигуры относительно осей y, x и обозначается соответственно Sy и Sx. Они равны сумме произведений площадей отдельных элементов фигуры на соответствующие

координаты их центроида: ^=1^-= Людмила Фирмаль

международной системе единиц измерения (Си) статический момент измеряется в кубических метрах (м3). Выражение (7.9)можно использовать для перезаписи выражения (7.7)для определения координат центроида плоскости: xc=Sy / a t US=$x!А — (7.Ага.) Если 64XC и XC равны нулю, то выбранные координатные оси проходят через

центроид фигуры и называются центральной координатной осью. В этом случае, поскольку D=y=OO, s y и Sx равны нулю. Таким образом, статический момент площади относительно центральной оси равен

• нулю. Из Формулы(7.10) следует, что статический момент площади этой фигуры относительно рассматриваемой оси будет равен произведению площади этой фигуры на кратчайшее расстояние от

центра тяжести до оси (рис.). 7.2). =^=DGS. (7.11) Используя формулу (7.11), можно определить статический момент площади данной фигуры относительно любой оси, если известно положение центра тяжести. Статический момент площади любой формы для

любой оси равен сумме статических моментов отдельных деталей для одной и Людмила Фирмаль

той же оси(рис. 7.2). — ■2л / Л=+^2+ • • •+ A p * p=

‘ g+ * * * +k=l (7.12) Где L — A2…, AP-площадь той части, где фигура разделена; pi » Z/2, UP-координата центра тяжести относительно оси//; S^.5, авг. . . Статический момент отдельных частей фигуры относительно оси Snx-X.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Статический момент площади плоской фигуры относительно оси способ вычисления

1. Вычисление объема тела

Пусть функция f ( x ; y ) ≥ 0. Рассмотрим тело, ограниченное поверхностью z = f ( x ; y ), плоскостью z = 0 и цилиндрической поверхно­стью, образующие которой па­раллельны оси 0 z , а направ­ляющей служит граница об­ласти D . Как было показано выше, согласно формуле (6.3) объем данного тела равен

Пример 6.9. Вычислить объём тела, ограниченного параболоидом z = x 2 + y 2 + 1, плоскостью x + y –3=0 и координатными плоскостями.

Решение. Основанием тела служит треугольник ОАВ. Область D в данном случае определяется неравенствами:

2. Вычисление площади плоской фигуры

Если положить в формуле (6.18) f ( x , y )=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой h = 1. Объем такого цилиндра,

как известно, численно равен площади S основания D . Получаем формулу для вычисления площади S области D :

или, в полярных координатах,

Пример 6.10. Вычислить площадь фигуры, ограниченной прямой y = 2 x + 1 и параболой y = x 2 + 1.

Решение. Решая совместно систему

Применяя формулу (6.19), будем иметь:

Решение. Переходим к полярной системе координат, полагая x = r cos φ и y = r sin φ ; тогда получаем

3. Вычисление массы плоской фигуры (пластины)

Масса плоской пластинки D с переменной плотностью γ =γ ( x , y ) находится по формуле

4. Определение статических моментов и координат центра тяжести плоской фигуры

Статические моменты фигуры D относительно осей 0 x и 0 y могут быть вычислены по формулам

а координаты центра масс фигуры – по формулам

Статические моменты широко используются в сопротивлении материалов и других технических науках.

5. Определение моментов инерции плоской фигуры

Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т.е. . Моменты инерции плоской фигуры относительно 0 x и 0 y могут быть вычислены по формулам:

Момент инерции фигуры относительно начала координат – по формуле

Пример 6.12 . Найти массу, статические моменты и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом и координатными осями. Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.

Решение. По формуле (6.21) находим массу пластины. По условию, γ =γ ( x , y )= k ∙ xy , где k – коэффициент пропорциональности.Тогда

Находим статические моменты пластинки по формулам (6.22):

Находим координаты центра тяжести пластинки, используя формулы (6.23):

6. Поверхностный интеграл I рода

Обобщением двойного интеграла является поверхностный интеграл. Пусть в трехмерном пространстве О xyz в точках некоторой поверхности площади S определена непрерывная функция u = f ( x ; y ; z ). Разобьем поверхность на конечное число n частей S_i , площади которых равны ∆ S_i , а диаметры – d_i , . Выберем в каждой части S_i произвольную точку M_i ( x_i ; y_i ; z_i ) и составим сумму произведений вида

Она называется интегральной суммой для функции f ( x ; y ; z ) по поверхности S . Если при интегральная сумма (6.26) имеет предел, который не зависит ни от способа разбиения поверхности S, ни от выбора точек M_i ( x_i ; y_i ; z_i ), то он называется поверхностным интегралом I рода от функции f ( x ; y ; z ) по поверхности S и обозначается . Следовательно,

Теорема 6.3 (о существовании поверхностного интеграла). Если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f ( x ; y ; z ) непрерывна на этой поверхности, то поверхностный интеграл существует

Формула (6.28)

выражает интеграл по поверхности S через двойной интеграл по проекции S на плоскость x 0 y . Отметим, что если поверхность S задана уравнением вида y=y(x;z) или x=x(y;z), то аналогично получим:

где D ₁ и D ₂ – проекции поверхности S на координатные плоскости xО z и y О z соответственно.

Пример 6.13. Вычислить , где S – часть цилиндрической поверхности , отсеченной плоскостями z = 0 и z = 3.

Решение . Из уравнения заданной цилиндрической поверхности выразим и учтём, что при x = 0 в плоскости x О y : . Так как частные производные равны , то согласно формуле (6.30), имеем

6.1. Площадь поверхности

Если поверхность S задана уравнением z = f ( x ; y ), a ее проекция на плоскость x 0 y есть область D , в которой z = f ( x ; y ), z_x ( x ; y ) и z_y ( x ; y ) – непрерывные функции, то ее площадь S вычисляется по формуле:

Пример 6.14. Вычислить площадь части плоскости x + y + z = 4, вырезаемой цилиндром x 2 + y 2 = 4 (рис. 6.10).

Чтобы вычислить этот интеграл, введём полярные координаты. Область D определяется: . Следовательно,

Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы γ =γ ( x ; y ; z ) . Все эти величины определяются одним и тем же способом:

– данную область разбивают на конечное число мелких частей;

– делают для каждой такой части предположения, упрощающие задачу;

– находят приближенное значение искомой величины;

– переходят к пределу при неограниченном измельчении разбиения области.

Проиллюстрируем описанный способ на примере определения массы материальной поверхности.

6.2. Масса поверхности

Пусть плотность распределения массы материальной поверхности есть γ =γ ( x ; y ; z ) . Для нахождения массы поверхности:

1. Разбиваем поверхность S на n частей S_i , , площадь которых обозначим ∆ S_i .

2. Выберем произвольную точку M_i ( x_i ; y_i ; z_i ) в каждой области S_i . Предполагаем, что в переделах области S_i плотность постоянна и равна её

4. Суммируя m_i по всей области, получаем: .

5. За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей S_i , то есть

6.3. Моменты и центр тяжести поверхности. С татические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:

Пример 6.15. Вычислить координаты центра тяжести однородной поверхности параболоида z = x 2 + y 2 , ограниченной плоскостью z = 1.

Решение. Вершина заданного параболоида совпадает с началом координат. Так как поверхность однородная (постоянная плотность массы), то, основываясь на ее симметрии, можно сделать вывод, что центр тяжести расположен на оси 0 z . Тогда x_c = 0, y_c = 0 и по формуле (6.36) аппликата . Пересечем параболоид поверхностью z = 1, спроектируем линию пересечения на плоскость x 0 y – получим окружность x 2 + y 2 =1 в качестве области D . Вычислим элемент поверхности параболоида z = x 2 + y 2 по формуле (6.31), учитывая, что :

Аналогично, переходя к полярным координатам на плоскости x 0 y , получим:

Источник