Старинный способ решения задач по способу магницкого

Решение задач на смеси и сплавы методом Магницкого

Рассматривается применение метода Магницкого «Рыба» при решении задач на смеси и сплавы.

Просмотр содержимого документа
«Решение задач на смеси и сплавы методом Магницкого»

ЗАДАЧИ НА СМЕСИ И СПЛАВЫ

«Для каждого ребенка должен индивидуально

проектироваться его «коридор ближайшего развития».

Понятие «ребенок, не способный к математике»

должно потерять смысл и исчезнуть из лексикона

учителей, родителей, школьников и общества».

Концепция развития математического

образования в Российской Федерации

В 2016 году я принимала участие в региональном этапе конкурса «Учитель года Дона-2016», при подготовке конкурсного урока по теме «Проценты», урок обобщения в 11 классе, я познакомилась с методом Магницкого при решении задач на смеси и сплавы. Меня заинтересовал этот метод, так как я уже много лет применяю мнемонические приемы на своих уроках. Я уверена, что использование мнемотехники дает возможность свободного выбора усвоения нового материала и развития индивидуальных мнемических процессов.

При подготовке к ЕГЭ в 2015-2016 учебном году я познакомила своих одиннадцатиклассников с методом Магницкого.

Результаты моих выпускников по решению задачи на смеси и сплавы на ЕГЭ по математике профильного уровня показали, что 68% справились с этой задачей, по России этот показатель составил 40% (http://fipi.ru/sites/default/files/document/1476454097/matematika.pd ).

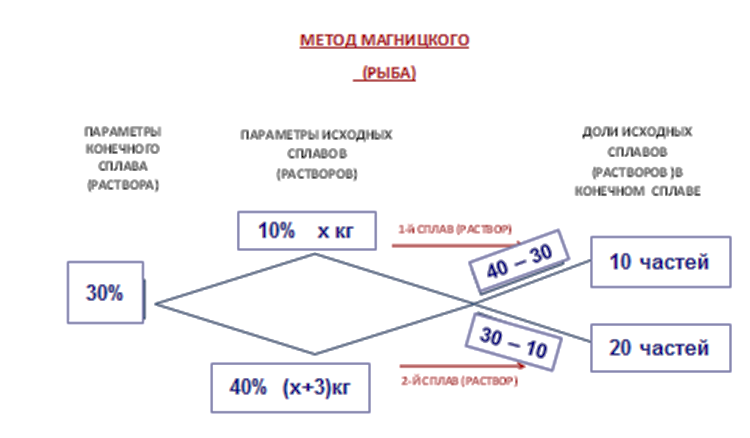
В основу метода Магницкого положено составление пропорции с помощью шаблона «Рыба».

Предлагаю рассмотреть решение задач:

Необходимо правильно внести данные в шаблон, от этого зависит успех решения задачи:

Когда «работаем» с концентрацией, то составляем разность: от большей величины вычитаем меньшую. Следующий шаг, составляем пропорцию 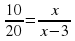и решаем ее. По условию задачи даем ответ на вопрос, выполняя необходимые вычисления.

В данной задаче неизвестна концентрация конечного продукта. Эти задачи вызывают у школьников затруднения при заполнении шаблона. Нужен дополнительный комментарий учителя, что величина концентрации полученного раствора больше концентрации данного раствора с меньшим процентным содержанием кислоты, но меньше концентрации данного раствора с большим процентным содержанием кислоты.

Составляем и решаем пропорцию: .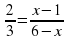

Составляем и решаем пропорцию: .

Данного вида задачи встречаются и в ОГЭ по математике в 9 классе, во II части, т.е. требуется представить развернутое решение. При оформлении решения с помощью шаблона «Рыба», не требуются «лишние» слова. В заполненной «Рыбе» видно, какая величина принята за «х», как с ней связаны остальные данные. Полученное уравнение в виде пропорции школьники решают лучше.

Задачи для самостоятельного решения:

1. В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

2. Имеется два сплава. Первый содержит 10% никеля, второй − 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

3. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 13% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

4.Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

5. Имеются два слитка, состоящие из цинка, меди и олова. Известно, что первый слиток массой 150 кг содержит 40% олова, а второй массой 250 кг — 26% меди. Процентное содержание цинка в обоих слитках одинаково. Сплавив первый и второй слитки, получили сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в полученном сплаве?

Н.А. Чупихина, МБОУ лицей №8, г. Кисловодск, Ставропольский край, «Решение задач на смеси и сплавы»

Источник

Старинный способ решения задач на смешивание (сплавление) любого числа веществ. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Леонтия Филипповича Магницкого (1703 г)

Старинный способ решения

задач на смешивание (сплавление) любого числа веществ. Задачам подобного типа уделялось значительное внимание в старинных рукописях и «Арифметике» Леонтия Филипповича Магницкого (1703 г).

(Леомнтий Филимппович Магнимцкий (при рождении Телятин; 9 (19) июня 1669, Осташков — 19 (30) октября 1739, Москва) — русский математик, педагог. Преподаватель математики в Школе математических и навигацких наук в Москве (с 1701 по 1739), автор первой в России учебной энциклопедии по математике).

Данный способ позволяет получить правильный ответ за очень короткое время и с минимальными усилиями.

Задача 1. Имеются два сплава с 72% содержанием меди и с 80% содержанием меди. Сколько грамм каждого сплава надо взять, чтобы получить 800г сплава с 75% содержанием меди?

Решим задачу 1 старинным способом.

Друг под другом пишутся процентные содержания меди в имеющихся сплавах, слева от них и примерно посередине – процентное содержание меди в сплаве, который должен получиться после сплавления. Соединив написанные числа черточками, получим такую схему:

Рассмотрим пары 75 и 72; 75 и 80. В каждой паре из большего числа вычтем меньшее, и результат запишем в конце соответствующей стрелочки. Получится такая схема:

Из нее делается заключение, что 72%-ного сплава следует взять 5 частей, а 80%-ного – 3 части 800:(5 + 3) = 100 г приходится на одну часть. Таким образом, для получения 800 г 75%-ного сплава нужно взять 72%-ного сплава 100·5 = 500 г, а 80%-ного – 100·3 = 300 г.

Задача 2. В каких пропорциях нужно сплавить золото 375-й пробы с золотом 750-й пробы, чтобы получить золото 500-й пробы?

Ответ: Нужно взять две части 375-й пробы и одну часть 750-й пробы.

Правило креста или квадрат Пирсона

(Карл (Чарлз) Пирсон (27 марта 1857, Лондон — 27 апреля 1936, там же) — выдающийся английский математик, статистик, биолог и философ; основатель математической статистики, автор свыше 650 опубликованных научных работ).

Очень часто при решении задач приходится встречаться со случаями приготовления растворов с определенной массовой долей растворенного вещества, смешением двух растворов разной концентрации или разбавлением крепкого раствора водой. В некоторых случаях можно провести достаточно сложный арифметический расчёт. Однако это малопродуктивно. Чаще для этого лучше применить правило смешения (диагональную модель «квадрата Пирсона», или, что тоже самое, правило креста).

Допустим, нужно приготовить раствор определенной концентрации, имея в распоряжении два раствора с более высокой и менее высокой концентрацией, чем нужно нам. Тогда, если обозначить массу первого раствора через m1, а второго – через m2, то при смешивании общая масса смеси будет складываться из суммы этих масс. Пусть массовая доля растворённого вещества в первом растворе – 1, во втором – 2, а в их смеси – 3. Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах:

m1∙1 + m2∙2 = 3(m1 + m2). Отсюда m1(1 – 3) = m2(3 – 2), .

Видно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворённого вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.

При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешения. При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.

щ1, щ2 – массовые части первого и второго растворов соответственно.

Для пояснения этого правила сначала решим простейшую задачу.

Задача 3. Морская вода содержит 5% соли (по массе). Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составила 1,5%?

Ответ: 7 килограммов.

Данный метод может использоваться и при решения задач на смеси и сплавы. Отлили часть раствора, отрезали кусок сплава. При этой операции остается неизменной концентрация веществ.

Таким образом, дополнительная работа по развитию и совершенствованию навыка решения задач на проценты имеет значимость не только для будущих абитуриентов, которые возможно встретятся с такими заданиями на ЕГЭ, но и для всех учащихся, так как современная жизнь неминуемо заставит в своей повседневности решать задачи на проценты.

Жизнь украшается двумя вещами: занятием математикой и ее преподаванием!
С. Пуассон

Источник

Старинный способ решения задач по способу магницкого

Арифметика Магницкого

Автор работы награжден дипломом победителя III степени

Обогащение науки и практики тесно связаны с глубоким анализом идей, накопленных человеческой цивилизацией в прошлые эпохи. Особый интерес в этом отношении представляет изучение творческого наследия Л.Ф. Магницкого, автора первого учебника математики «Арифметика» в России. А ведь учебник- это источник знаний! В течение полстолетия книга с честью выполняла свою роль, став пособием русских людей, которые стремились к математическому образованию. Об авторе и этой замечательной книге, к сожалению, современные ученики, живущие в постиндустриальном мире XXI века, знают немного. Я решила проверить, действительно ли это так или я ошибаюсь. Проведя социологический опрос среди учащихся своего класса, «Знаете ли вы автора первого учебника математики в России?», я убедилась в том, что моё предположение подтвердилось. Я собрала, изучила материал по данной теме, решила некоторые задачи из учебника «Арифметика» и на классном часе решила рассказать одноклассникам о великом русском математике Л.Ф. Магницком и о роле «Арифметики» в России, тем самым пополнить их знания в истории математики.

Проблема: отсутствие у учащихся знаний о великом математике Л.Ф. Магницком и о первом российском учебнике по математике «Арифметика».

Цель исследования: изучить творчество Л.Ф. Магницкого и показать роль первого печатного учебника «Арифметика» в России.

1.Провести социологический опрос.

2.Собрать информацию об интересующем нас учёном- математике Л.Ф. Магницком, его учебнике «Арифметика», информацию о старинных мерах длины, денежных единицах.

3.Проследить за развитием математической мысли на Руси.

4.Продемонстрировать приёмы решения задач и показать значимость «Арифметики» Магницкого.

5.Познакомить одноклассников с биографией Л.Ф.Магницкого и с решением некоторых задач из учебника «Арифметика».

Задачи из учебника Л.Ф. Магницкого оказались весьма жизнеспособными, многие из них перешли в последующие учебники, и до настоящего времени они часто приводятся авторами арифметических и алгебраических задачников. Эти задачи весьма интересны, они дают возможность почувствовать колорит и особенности языка той эпохи. Поэтому, я считаю, что выбранная мною проблема актуальна в наше время.

Объект исследования: математик Л.Ф. Магницкий.

Предмет исследования: биография Магницкого, книга «Арифметика», его задачи.

Если я изучу биографию Л.Ф. Магницкого и способы решения задач, я смогу рассказать учащимся нашего класса о роли математики в современном обществе. Это будет увлекательно и повысит интерес к изучению математики.

Методы исследования: социологический опрос, поисковый, теоретико-практический, анализ и синтез источников информации, самостоятельное решение задач.

Новизна данной работы заключается в демонстрации приёмов решения задач, с использованием денежных величин, старинной меры длины, посвящённые вопросам хронологии и календаря которые не рассматриваются в школьных учебниках.

Обзор изучаемой литературы

В ходе работы я столкнулась с тем, что книги «Арифметика» Магницкого нет в переизданном виде. Приходилось брать много информации из справочной литературы. Использовала исторические материалы о замечательном учёном, различные пособия, энциклопедии по математике, а также электронные пособия и Интернет- ресурсы, откуда узнала биографию и творческий путь Л.Ф. Магницкого, роль учебника «Арифметика» в России.

Глава 1. Биография Леонтия Филипповича Магницкого

1.1 Биографические сведения о Л. Магницком
Леонтий Филиппович Магницкий

Русский математик, педагог. Преподаватель математики в Школе математических и навигацких наук в Москве, автор первого в России учебного пособия по математике.

Родился: 9 июня 1669 г., Осташков

Умер: 30 октября 1739 г. (70 лет), Москва

В браке с: Мария Гавриловна

Дети: Иван Леонтьевич

Магницкий Леонтий Филиппович (1669—1739), математик, педагог.

В 1932 году при постройке московского метро на глубине одного метра обнаружилась плита из крепкого известняка, на обратной стороне которой оказалась тонко выбита «эпитафия» надгробия Л. Ф. Магницкого, написанная его сыном Иваном:

«В вечную память христианину, благочестно, целомудренно, благоверное и добродетельно пожившему Леонтию Филипповичу Магницкому, первому в России математики учителю, здесь погребенному, (. ) который путь его временного и прискорбного жития начал 1669 года июня 9-го дня, наукам изучался дивным и неудобовероятным способом, (. ) и от Его Величества, по усмотрению нрава ко всем приятнейшего и к себе влекущего, пожалован прозванием Магницкий и учинён российскому благородному юношеству учителем математики. В котором звании ревностно, верно, честно, всеприлежно и беспорочно служа четырём самодержцам всероссийским и прожив в мире 70 лет, 4 месяца и 10 дней, 1739 года, октября 19-го дня, о полуночи в 1 часу, оставят добродетельным своим житием и благовестною христианскою кончиною пример жития отставшим по нем, (. )» (в сокращении).

На другой день под плитой-памятником на глубине четырёх метров обнаружена была гробница. Она была выложена из хорошего кирпича и залита со всех сторон известью. В могиле находилась дубовая колода, в ней лежал невредимый скелет Леонтия Филипповича с некоторыми сохранившимися на нём покровами, под головой находилась стеклянная чернильница, имевшая форму лампадки, и рядом лежало полуистлевшее гусиное перо.

О создателе уникального учебника, Леонтии Магницком, известно не так уж и много. Основными источниками биографии Л. Магницкого являются: некоторые тверские архивные материалы, частично опубликованные; археографические источники, связанные с московской Математико-навигацкой школой; отдельные архивные документы, а также надписи на надгробиях Магницкого и его жены, выполненные их сыном Иваном.

Большинство сведений о нем относится к годам, когда он уже преподавал в Навигационной школе.

1.2 Детство и юность 1 Леонтия Магницкого

О детских годах известно лишь то, что родился он в крестьянской семье в Осташковской монастырской слободе на берегу озера Селигер. Отца будущего математика звали Филиппом, прозвище его было Теляшин, фамилии же в то время крестьянам не полагались. Мальчик еще в детстве научился самостоятельно читать, благодаря чему временами исполнял обязанности псаломщика в местной церкви.

Судьба юноши резко изменилась, когда из родной слободы его отправили с возом мороженой рыбы в Иосифо-Волоколамский монастырь. Видимо, в монастыре паренек проявил интерес к книгам, и игумен, убедившись в его грамотности, оставил Леонтия чтецом. Уже через год игумен благословил юношу на учебу в Славяно-греко-латинскую академию, бывшую в тот период основным учебным заведением в России. В академии Леонтий проучился около восьми лет.

Любопытно, что математику, которой Магницкий затем занимался до конца жизни, в академии не преподавали. Следовательно, её Леонтий изучил самостоятельно, как и основы навигации и астрономии. Закончив академию, Леонтий не стал постригаться в священнослужители, как надеялся отправлявший его на учебу игумен, а стал преподавать математику, а, возможно, и языки, в семьях московских бояр.

1.3 Происхождение фамилии

В Москве и произошла его встреча с Петром I, который умел находить людей, полезных для России, из каких бы слоев общества они ни происходили. Безродный учитель, не имевший даже фамилии, понравившийся царю глубокими знаниями, получил от монарха своеобразный подарок. Петр повелел ему впредь именоваться Магницким 2 , так как он притягивал своей ученостью отроков к себе, как магнитом.

Цитата: «из уст Петра поименован из Теляшина Магницким, в сравнении того, как магнит привлекает к себе железо, так он природными и самообразованными способностями своими обратил внимание на себя». Для современных людей значимость этого подарка не совсем понятна, а ведь в то время фамилии имели только представители высшей знати.

Глава 2. Арифметика Магницкого

2.1 Об арифметике

«Арифметика, сиречь наука числительная. С разных диалектов на славянский язык переведённая, и в едино собрана и на две книги разделена. Ныне же повелением благочестивейшего Великого Государя нашего царя и Великого Князя Петра Алексеевича всея Великие и Малые и Белые России самодержца. При благороднейшем, Великом Государе нашем царевиче и великом князе Алексии Петровиче, в богоспасаемом царствующем великом граде Москве типографским тиснением ради обучения мудролюбивых российских отроков, и всякого чина и возраста людей на свет произведена первое, в лето от сотворения мира 7211, от рождества же по плоти Бога слова 1703, индикта 11 месяца ианнуария. Сочинил сия книга чрез труды Леонтия Магницкого.» 3
Так начинается первый в России учебник математики, который появился более 300 лет назад в январе 1703 года . Его автором был Леонтий Филиппович Магницкий (1669 — 1739) преподаватель, созданной по указу Петра I «Школы математических и навигационных наук». В этом труде кроме сведений по арифметике, содержались начала алгебры, геометрии и тригонометрии, а также практические расчеты по коммерческим вычислениям, технике и навигации. Книга состояла из 326 листов, т.е. из 652 страниц, включая заглавный лист и 3 листа гравюр на меди. Кроме того, к книге еще отдельно приложены 5 листов с таблицами. Печать двухцветная — красная с черным: все страницы — в рамках из наборных украшений. Фронтиспис с изображением Аристотеля и Пифагора и две остальные гравюры на меди выполнены Михаилом Карновским.

Начальная, гравированная на дереве аллегорическая заставка изображает Арифметику в виде женщины, сидящей на престоле в храме наук. Книга снабжена многочисленными чертежами и табличками.

М. В. Ломоносов назвал эту первую отечественную печатную учебную книгу «вратами своей учености».

2.2. «Арифметика» Леонтия Магницкого

До петровского времени государственной системы образования не существовало. В августе 1701 года Пётр I издал указ об открытии в Москве Школы навигационных наук: нарождавшаяся морская держава нуждалась в грамотных корабелах и мореходах. Преподавать в новой школе, расположившейся в Сухаревой башне («ради смотрения в совершенстве горизонта на месте высоком»), были приглашены профессор А. Д. Фарварсон, учителя С. Гвин, Р. Грейс и «помоществователь» Леонтий Филиппович Магницкий.

Один из первых выпускников Славяно-греко-латинской академии, изучивший, помимо академических предметов, немецкий, голландский и итальянский языки, Магницкий вскоре заявил о себе как об образованнейшем человеке и хорошем преподавателе точных наук. Дьяк Оружейной палаты А. А. Курбатов, присматривавший за школой, докладывал царю, что «рыцари» Гвин и Грейс, «хотя и навигаторы написаны, только и до Леонтия наукою не дошли». Неслучайно именно Магницкому было велено «через труд свой издать на словенском диалекте, избрав от арифметики, и геометрии, и навигации, поелику возможно, годную к тиснению книгу». Так в январе 1703 года появилась «Арифметика, сиречь наука числительная».

По содержанию она представляла собой своеобразную энциклопедию, включавшую сведения об арифметике, алгебре, геометрии, тригонометрии, астрономии, геодезии, навигации. О форме изложения материала свидетельствовало уже начало книги: «Что есть арифметика? ¨C Арифметика, 1-ти числительница, есть художество честное, независтное и всем удобопонятное, многополезнейшее».

Учебник Магницкого впервые вводил в широкий обиход арабские цифры вместо прежних буквенных обозначений чисел. «Что есть нумерация? ¨C вопрошалось в одном из начальных параграфов „Арифметики“. ¨C Нумерация есть счисление, еже совершенно вся числа речию именовати, яже в десяти знаменованиях или изображениях содержатся и изображаются сице: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, ¨C из них же девять незнаменательны суть, последнее же 0 (еже цифрою или ничем именуется), егда убо оно едино стоит, тогда само о себе ничто же значит; егда же коему оних знаменований приложено будет, тогда умножает вдесятеро».

В XVII и начале XVIII века математика считалась очень трудным предметом. Если она вводилась в школьную практику, то лишь в старших классах. Арифметическое деление оставалось недоступным для многих. Вплоть до XVIII века ни в России, ни на Западе почти не встречается учебников по арифметике. В обращении находились ученые сочинения, усвоение которых предназначалось для особых любителей математических вычислений.

Автор каждого учебника математики до Магницкого стремился обнять всю математику, не делая принципиального различия между ее отделами. В сочинении Магницкого в одно гармоническое целое были соединены не только арифметика, геометрия, тригонометрия, но и астрономия, понятия о вычислении тригонометрических таблиц, необходимые начальные сведения из геодезии и навигации. Впервые для русской и иностранной литературы приведены градусы широты и долготы Москвы, Киева, Архангельска и Астрахани.

Вышла «Арифметика» в январе 1703 г., как о том сказано на титульном листе книги. Итак, от начала оплачиваемой работы до факта издания прошло почти два года.

Полное название учебника: «Арифметика, сиречь наука числительная. С разных диалектов на славенский язык преведеная, и во едино собрана, и на две книги разделена». Упомянутые в названии две книги имеют следующие наименования: «Арифметика политика, или гражданская» и «Арифметика логистика не по гражданству токмо, но и к движению небесных кругов принадлежащая».

Первая книга разделена на пять частей. Начальная из них содержит сведения о нумерации и четырех арифметических действиях с целыми числами, раздел о денежном счете, мерах и весах, следующая посвящена дробям. Третья и четвертая к практическим задачам. В последней рассматриваются (в применении к морскому и военному делу) алгебраические правила, прогрессии и корни. В завершение даются десятичные дроби, которые были внове для соответствующей учебной литературы.

Вторая книга (арифметика-логистика) поделена на три части. В первой речь идет о квадратных уравнениях. Вторая посвящена геометрии и тригонометрии: задачам на измерение площадей, теоремам на тригонометрические функции различных углов. Заключительная часть относится к математическим основам навигации «Обще о земном размерении и яже к мореплаванию надлежит». Здесь рассматривается математическое приложение к мореплаванию уже полученных сведений по арифметике, алгебре, геометрии и тригонометрии. При помощи прилагаемых таблиц решается навигационная задача определения широты места по наклонению магнитной стрелки, рассчитывается время приливов и отливов и пр.

Математические задачи основываются на близких тогдашнему читателю примерах из земледельческого и воинского быта. Некоторые задачи и примеры, использованные Магницким, вошли в современные школьные учебники. Автор постоянно напоминает, что все рассматриваемые действия, правила, примеры имеют практическое приложение: случаи, «бывающие в гражданстве» («купецкая всякая действа, яже во всяких куплях, продажах, менах, сложениях и делениях. в заимодавствах, и платежах. во убытках и прибытках и во всяких действах. » «И от сего величайшая полза, всякому чину, не токмо купецкому, но и воинскому, и икономам, и всякому и везде сущему человеку. «).

Излагается материал в «Арифметике» 4 Магницкого в вопросно-ответной форме; например, глава о вычитании целых чисел начинается так: «Что есть субстракция? Субстракция, или вычитание есть, также малое число из большого вычитаем и излишнее объявляем K яко егда случится тебе ситцев перечень 57 вычитати из 89, и оставшееся объявить; и ты поставь меньший перечень под большей сице 89 57, прочертив же под ними черту, якоже есть 57, и начни вычитати от правой руки, умствуй 7 из 9, останется 2 еже постави против 7 под чертою

потом таки умствуй 5 из 8 останется 3: и ты тое постави против 5 под чертой же

и объяви излишнее большего перечня пред меньшим под чертой».

Магницкий впервые ввел термины «множитель», «делитель»,

«произведение», «извлечение корня», а также заменил устаревшие слова «тьма, легион» словами «миллион, биллион, триллион, квадриллион».

Главным педагогическим достоинством «Арифметики» является доступность изложения и занимательность. И Магницкий использовал любую возможность привлечь внимание читателей всевозможными курьезными случаями из мира чисел. Разбирая арифметические примеры, сопровождающиеся акростихами, гравюрами с изображениями царицы-арифметики, восседающей на троне, основателей этой науки Архимеда и Пифагора и другими, стихотворными высказываниями и поучениями («. Архимед и Пифагор, излиша мудрости яко воды от гор», «К двум един то есть три, два же к трем пять смотри. Так и все назирай, таблицу разбирай»), невольно поддаешься обаянию магии цифр. Многие приемы, изложенные в учебнике (умножение «на пальцах», вычисление квадратных и кубических корней без применения специальных таблиц, столбиком) применимы и сегодня.

«Ахиллесовой пятой» математического образования того времени является слабая его связь с практикой, жизнью. Содержание «Арифметики» довольно тесно связано с жизнью через кораблевождение. По данным, основанным на долголетних исследованиях российских историков астрономии и навигации, «Арифметика» Магницкого стала практическим пособием для всех путешественников и мореплавателей с 1703 г.

2.3 Единицы измерений, используемые в учебнике Магницкого

Верста межевая = 2 верстам путевым = 1000 саженям = 2,160 км.

Верста путевая = 500 саженям =1,080 км.

Сажень = 3 аршинам = 12 четвертям = 48 вершкам = 216 см.

Аршин = 4 четвертям = 16 вершкам = 72 см.

Четверть (пядь) = 4 вершкам = 18 см.

Меры поверхности (площади).

В переводе на метрическую систему казенная десятина XVII в. в 2400 квадратных сажен равнялась 11 197,44 кв. м, или 1 га и 1197,44 кв. м.

Система поземельных мер Русского государства представляется в следующем виде:

Десятина = 2 четвертям = 4 осьминам = 8 полось-минам = 16 четверикам.

Четверть = 2 осьминам = 4 полосьминам = 8 четверикам = 3 третникам.

Осьмина = 2 полосьминам = 4 четверикам.

В Русском централизованном государстве употреблялись следующие меры сыпучих тел: четверть = 2 осьминам = 8 четверикам

В 1679 г. объем казенной четверти был увеличен до 8 пудов ржи

Вощаная четверть = 12 пудам. . Берковец = 10 пудам.

Контарь = 2,5 пуда.

Пуд = 16 безменам = 40 большим гривенкам, или фунтам = 80 малым гривенкам.

Большая гривенка = 2 малым гривенкам = 4 полугривенкам малым = 96 золотникам.

Малая гривенка = 2 полугривенкам малым = 48 золотникам.

Полугривенка малая = 24 золотникам.

Основными мерами веса являлись: для более крупного веса пуд, для более мелкого веса фунт с его частями. Драгоценные металлы и камни взвешивались золотниками и почками.

В переводе на десятичную систему мер пуд весил 16,38 кг, фунт — 409,512 г, золотник 4,267 г.

Мера измерения жидких тел

Мерник, или бочка = 40 ведрам = 4 десятням.

Десятня = 10 ведрам.

Ведро = 2 полуведрам = 4 четвертям ведра = 6 шестерикам.

Ведро = 8 кружкам = 16 полукружкам = 32 четвертям кружки.

Ведро = 10 кружкам.

Кружка = 10 чаркам.

Ведро около 12,5 кг воды.

Кружка = около 1,5 кг воды.

Фунтовик = 2 полуфунтовикам.

Полуфунтовик = 5 водочным копеечникам.

Денежный счет Русского централизованного государства сложился на рубеже XV-XVI вв. Он включал в себя три основные счетные единицы рубль, алтын и деньгу. Встречалась и четвертая единица полушка, равная половине деньги:

Рубль = 33 алтынам 2 деньгам = 200 деньгам. Алтын = 6 деньгам. Деньга = 2 полушкам.

Это официальный счет. Но наряду с ним встречалось и другое деление рубля:

1 рубль = 2 полтинам = 4 полуполтинам (четвертинам) = 10 гривнам = 200 деньгам.

Полтина = 2 полуполтинам = 5 гривнам =100 деньгам.

Полуполтина = 2,5 гривнам = 50 деньгам. Гривна = 20 деньгам.

Все названные единицы были счетными. Монетных же было всего три: Копейка = 2 деньгам. Деньга = 2 полушкам. Полушка = 0,5 деньги

2.4 Задачи из «Арифметики» 5 Л.Ф. Магницкого

Некто оставил в наследство жене, дочери и трем сыновьям 48000 тысяч рублей и завещал жене 1/8 всей суммы, а каждому из сыновей вдвое больше, чем дочери. Сколько досталось каждому из наследников?

48000:8=6000 (руб.) – завещал жене

48000-6000=42000 (руб.) – завещал детям

Пусть х — сумма денег, завещанная дочери, тогда 2х — сумма денег завещанная каждому из сыновей.

х=6000 (руб.) – некто завещал дочери

2*6000=12000 (руб.) – некто завещал каждому из сыновей

Ответ: некто завещал жене 6000 рублей, дочери 6000 рублей и 3-м сыновьям по 12000 каждому.

Капитан на вопрос: “Сколько он имеет в своей команде людей?”- отвечал: “На лицо 9 человек, то есть 1/3 команды, остальные в карауле”. Сколько в карауле?

9*3=27 (чел.) – вся команда

27-9=18 (чел.) – в карауле

Ответ: в карауле 18 человек.

Некий купец купил колокол весом 2546 пудов. А за всякий пуд дати по 550 копеек, и восхотев ведати, какая цена за вест колокол будет?

550*2546=1400300 (копеек) или 14003 рубля

Ответ: 14003 рубля будет за вест колоко.

Некто пришел в яд, купил игрушек для малых ребят. За первую игрушку заплатил 1/5 часть своих денег, за вторую 3/7 остатка от первой покупки. По приезде в дом нашел в кошельке денег 1 рубль 92 копейки. Спрашивается, сколько было в кошельке?”

1 рубль 92 копейки = 192 копейки .

Пусть х сумма денег оставшаяся после первой покупки, тогда после второй покупки осталось х*4/7.

х=336 (коп.) — осталось после первой покупки

336 копеек = 4/5 всех денег в кошельке

420 копеек= 4 рубля 20 копеек

Ответ: в кошельке было 4 рубля 20 копеек.

Скажите мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твою беседу?». «-Вот сколько, — ответил Пифагор, — половина изучают математику, четверть ¨C музыку, седьмая часть пребывает в молчании, и кроме того, есть ещё три женщины. Итак, сколько учеников было у Пифагора?”

Пусть х — число учеников Пифагора, тогда
x — (1/2 + 1/4 + 1/7)x = 3

x – (14/28 + 7/28 +4/28)x=3

Ответ: у Пифагора было 28 учеников.

Лошадь съедает воз сена за месяц, коза за два месяца, овца за три месяца. За какое время лошадь, коза и овца вместе съедят такой воз сена?

Чтобы получить целое количество возов сена, возьмем период 6 месяцев и узнаем сколько животные съедят за это время.

Лошадь — 6 возов, коза — 3 воза, овца — 2 воза. Вместе — 11 возов.

1 воз = 6:11= 6/11 месяца

Ответ: 1 воз сена лошадь, коза и овца съедят за 6/11 месяца.

Лев может съесть овцу за 2 часа, волк за 3 часа, а собака за 6 часов. За какое время они вместе съели бы овцу?

Надо найти целое число, за которое каждый из них съел хотя бы 1 овцу. Нам подходит число 6, так как именно за это время собака съедает 1 одну овцу.

За 6 часов лев съест 3 овцы, волк 2 овцы, а собака 1. Вместе они за 6 часов съедают 6 овец. Значит, 6:6=1.

Ответ: за 1 час лев, волк и собака вместе съедят одну овцу.

Купил некто трех сукон 108 аршин; единого взял 12-ю больше перед другим, а другого 9-ю больше перед третьим, и ведательно есть, колико коего сукна взято было.

Пусть х — аршин 1-го сукна , тогда 2-го (х+12), а 3-го (х+12+9) и всего купили (х+х+12+х+12+9) аршин, а по условию общее количество — 108, тогда

х=25(аршин) — купили 1-го сукна

25+12=37 (аршин) — купили 2-го сукна

25+12+9=46 (аршин) — купили 3-го сукна

Ответ: некто купил 1-го сукна 25 аршин, 2-го сукна 37 аршин, а 3-го 46 аршин.

Один человек выпьет кадь пития в 14 дней, а со женою выпьет ту же кадь в 10 дней, и ведательно есть, в колико дней жена его особо выпьет ту же кадь.

В один день муж выпивает1/14 кади, за 10 дней он выпивает 10/14, выходит, что его жена за 10 дней выпивает 4/14 кади или 2/7.

1 (кадь)=2/7+2/7+2/7+1/7, т. е. 3 раза по 10 дней и половина 10-ти дней, т. е. 5 дней

10 + 10 +10 +5 = 35 (дней)

Ответ: жена выпьет одну кадь пития за 35 дней.

Один путник идет от града в дом, а ходу его будет 10 дней, а другой от дому в град тот же путь творящее, может пройти в 15 дней, оба же сии человека пойдоша во един и тот же час от мест своих, и ведательно есть, в колико дней сойдутся.

Первый путник за 1 день проходит 1/10 части пути, а второй 1/15 части пути. Пусть х – количество дней, через которое они встретятся, тогда 1-й путник пройдет х*1/10, а 2-й х*1/15.

Ответ: путники встретятся через 6 дней.

В некоей единой мельнице были трои жерновы, и едины жерновы в сутки могут смолоти 60 четвертей, а другие в толикое же время могут смолоти 54 четверти, третьи же в толикое же время могут смолоти 48 четвертей, и некий человек даде жита 81четверть, желал в скорости оно смолоти, и насыпа на все три жерновы, и ведательно есть, в колико часов оно жито смолотися и колико на всякие жерновы достоит мельнику насыпати.

Решение: 60+54+48= 162 (четверти) – могут смолоть все 3 жернова за сутки.

81/162=1/2 (суток) – смелют все 3 жернова 81 четверть

½ *60=30 (четверт.) – смелет 1-й жернов

½*54=27(четверт.) – смелет 2-й жернов

½*48=24(четверт.) – смелет 3-й жернов

Ответ: 81 четверь жита все три жернова смелят за пол суток, 1-й жернов смелет 30 четвертей, 2-й жернов смелет 27 четвертей, 3-й жернов смелет 24 четвертей.

В жаркий день 6 косцов выпили бочонок кваса за 8 часов. Нужно узнать, сколько косцов за 3 часа выпьют такой же бочонок кваса.

В один день муж выпивает1/14 кади, за 10 дней он выпивает 10/14, выходит, что его жена за 10 дней выпивает 4/14 кади или 2/7.

1 (кадь)=2/7+2/7+2/7+1/7, т. е. 3 раза по 10 дней и половина 10-ти дней, т. е. 5 дней

10 + 10 +10 +5 = 35 (дней)

Ответ: жена выпьет одну кадь пития за 35 дней

Некий человек нанял работника на год, обещал ему дати 12р. и кафтан, но тот, проработав 7 месяцев, восхотел уйти и просил достойные платы с кафтаном. Он же даде ему по достоинству расчет 5р. и кафтан, и ведательно есть, какой цены оный кафтан был?

1/12 кафтана — в 1 месяц

за 7 месяцев надо было заплатить 7 рублей, а дали 5

1) 7-5=2 (руб.)=200 (коп.) — стоит недостающая часть кафтана

2) 200:5=40 (коп.) — 1/12 кафтана

3) 40х12=480 (коп.) =4 руб. 80 коп. — стоит кафтан

Ответ: кафтан стоит 4 рубля 80 копеек.

Арифметика Магницкого появилась в тот период, когда царь Петр I спешил увеличить число образованных граждан в России, создавая новые учебные заведения для обучения навигацкому делу, строительному, медицинскому и др. Царь Петр I для распространения математических знаний в 1714 году открывает много цифирных школ для преподавания молодым отрокам математических наук, что тоже способствовало повышению образовательного уровня граждан России и формированию новых образовательных стандартов для государственных служащих и военных.

Историческое значение Арифметики Магницкого, как учебного пособия по математике, в том, что он вводит удобную, схожую с арабской, нумерацию, записывает передовые алгоритмы того времени сложения, вычитания, умножения, деления. Изложение материала опирается на решение практических задач, что позволяет использовать учебник для самообразования.

Я составила сборник задач из «Арифметики Магницкого». Результаты исследования могут быть использованы для дополнительных занятий по математике в форме факультативов, как дополнительный материал к урокам. Считаю, что цель, которую я ставила перед собой достигнута.

Список литературы и интернет-ресурсов

Арифметика Магницкого. Точное воспроизведение подлинника. С приложением статьи П. Баранова. — М.: Издание П. Баранова, 1914. URL: http://elibrary.orenlib.ru/index.php?dn=down&to=open&id=1261

Беленчук Л.Н., Просвещение в эпоху Петра Первого// Отечественная и зарубежная педагогика. И. Институт стратегии развития образования Российской академии образования. — 2016. — № 3 (30). — С. 54-68. URL:http://elibrary.ru/download/elibrary_26286817_93418862.pdf

Денисов А.П., Леонтий Филиппович Магницкий (1669–1739)// М.: Просвещение. — 1967. — 143 с.

Магницкий Леонтий Филиппович// Энциклопедический словарь Брокгауза и Эфрона:В 86 томах (82 т. и 4 доп.), Санкт-Петербург: 1890-1907.

Малых А.Е., Данилова В.И,, Леонтий Филиппович Магницкий (1669–1739)// Вестник Пермского университета, Математика. Механика. Информатика. – 2010. – Вып. 4 (4). – С. 84-94. URL:http://elibrary.ru/download/elibrary_15624452_71219613.pdf

Степаненко Г.А., Арифметика Магницкого и современные учебники математики начальной школы// Таврический научный обозреватель, И. Общество с ограниченной ответственностью «Межрегиональный институт развития территорий», г. Ялта. – 2016. – 1-3 (6) – С. 38-43. URL : http://elibrary.ru/download/elibrary_25473094_94425485.pdf

Тихонова О. Ю. Леонтий Филиппович Магницкий – математик и христианин // Научно-методический электронный журнал «Концепт». – 2016. – № 3 (март). – С. 71–75. – URL:http://e-koncept.ru/2016/16053.htm

Чекин А.Л., Борисова Е.В., Первый отечественный печатный учебник «Арифметика» Л.Ф. Магницкого// Журнал «Начальная школа», И. Общество с ограниченной ответственностью Издательство «Начальная школа и образование», г. Москва. – 2013. — №9. – С.12-15.

http://museum.lomic.ru/trip.html — сайт музея М.В. Ломоносова в селе Ломоносово.

Сборник, составленный из задач, приведенных в «Арифметике» Л. Магницкого.

Некто оставил в наследство жене, дочери и трем сыновьям 48000 тысяч рублей и завещал жене 1/8 всей суммы, а каждому из сыновей вдвое больше, чем дочери. Сколько досталось каждому из наследников?

Капитан на вопрос: “Сколько он имеет в своей команде людей?”- отвечал: “На лицо 9 человек, то есть 1/3 команды, остальные в карауле”. Сколько в карауле?

Некий купец купил колокол весом 2546 пудов. А за всякий пуд дати по 550 копеек, и восхотев ведати, какая цена за вест колокол будет?”

Некто пришел в ряд, купил игрушек для малых ребят. За первую игрушку заплатил 1/5 часть своих денег, за вторую ¨C 3/7 остатка от первой покупки. По приезде в дом нашел в кошельке денег 1 рубль 92 копейки. Спрашивается, сколько было в кошельке?”

Скажите мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твою беседу?». «-Вот сколько, — ответил Пифагор, — половина изучают математику, четверть ¨C музыку, седьмая часть пребывает в молчании, и кроме того, есть ещё три женщины. Итак, сколько учеников было у Пифагора?”

Лошадь съедает воз сена за месяц, коза ¨C за два месяца, овца ¨C за три месяца. За какое время лошадь, коза и овца вместе съедят такой воз сена?

Лев может съесть овцу за 2 часа, волк ¨C за 3 часа, а собака ¨C за 6 часов. За какое время они вместе съели бы овцу?

Купил некто трех сукон 108 аршин; единого взял12-ю больше перед другим, а другого 9-ю больше перед третьим, и ведательно есть, колико коего сукна взято было.

Один человек выпьет кадь пития в 14 дней, а со женою выпьет ту же кадь в 10 дней, и ведательно есть, в колико дней жена его особо выпьет ту же кадь.

Один путник идет от града в дом, а ходу его будет 10 дней, а другой от дому в оград тот же путь творящее, может пройти в 15 дней, оба же сии человека пойдоша во един и тот же час от мест своих, и ведательно есть, в колико дней сойдутся.

В некоей единой мельнице были трои жерновы, и едины жерновы в сутки могут смолоти 60 четвертей, а другие в толикое же время могут смолоти 54 четверти, третьи же в толикое же время могут смолоти 48 четвертей, и некий человек даде жита 81четверть, желал в скорости оно смолоти, и насыпа на все три жерновы, и ведательно есть, в колико часов оно жито смолотися и колико на всякие жерновы достоит мельнику насыпати.

В жаркий день 6 косцов выпили бочонок кваса за 8 часов. Нужно узнать, сколько косцов за 3 часа выпьют такой же бочонок кваса.

Некий человек нанял работника на год, обещал ему дати 12р. и кафтан, но тот, проработав 7 месяцев, восхотел уйти и просил достойные платы с кафтаном. Он же даде ему по достоинству расчет 5р. и кафтан, и ведательно есть, какой цены оный кафтан был?

48000:8=6000 (руб.) — завещал жене

48000-6000=42000 (руб.) — завещал детям

Пусть х — сумма денег, завещанная дочери, тогда 2х — сумма денег завещанная каждому из сыновей.

х=6000 (руб.) — некто завещал дочери

2*6000=12000 (руб.) — некто завещал каждому из сыновей

Ответ: некто завещал жене 6000 рублей, дочери 6000 рублей и 3-м сыновьям по 12000 каждому.

9*3=27 (чел.) — вся команда

2) 27-9=18 (чел.) — в карауле

Ответ: в карауле 18 человек.

550*2546=1400300 (копеек) или 14003 рубля

Ответ: 14003 рубля будет за вест колокол

1 рубль 92 копейки = 192 копейки

Пусть х сумма денег оставшаяся после первой покупки, тогда после второй покупки осталось х*4/7.

х=336 (коп.) — осталось после первой покупки

336 копеек = 4/5 всех денег в кошельке

420 копеек= 4 рубля 20 копеек

Ответ: в кошельке было 4 рубля 20 копеек

Пусть х — число учеников Пифагора, тогда
x — (1/2 + 1/4 + 1/7)x = 3

x – (14/28 + 7/28 +4/28)x=3

Ответ: у Пифагора было 28 учеников

Чтобы получить целое количество возов сена, возьмем период 6 месяцев и узнаем сколько животные съедят за это время.

Лошадь — 6 возов, коза — 3 воза, овца — 2 воза. Вместе — 11 возов.

1 воз = 6:11= 6/11 месяца

Ответ: 1 воз сена лошадь, коза и овца съедят за 6/11 месяца

Надо найти целое число за которое каждый из них съел хотя бы 1 овцу. Нам подходит число 6, так как именно за это время собака съедает 1 одну овцу.

За 6 часов лев съест 3 овцы, волк 2 овцы, а собака 1. Вместе они за 6 часов съедают 6 овец. Значит

Ответ: за 1 час лев, волк и собака вместе съедят одну овцу

Пусть х — аршин 1-го сукна ,тогда 2-го (х+12), а 3-го (х+12+9) и всего купили (х+х+12+х+12+9) аршин, а по условию общее количество — 108, тогда

х=25(аршин) — купили 1-го сукна

25+12=37 (аршин) — купили 2-го сукна

25+12+9=46 (аршин) — купили 3-го сукна

Ответ: некто купил 1-го сукна 25 аршин, 2-го сукн 37 аршин, а 3-го 46 аршин

В один день муж выпивает1/14 кади, за 10 дней он выпивает 10/14, выходит что его жена за 10 дней выпивает 4/14 кади или 2/7.

1 (кадь)=2/7+2/7+2/7+1/7, т. е. 3 раза по 10 дней и половина 10-ти дней, т. е. 5 дней

10 + 10 +10 +5 = 35 (дней)

Ответ: жена выпьет одну кадь пития за 35 дней

Первый путник за 1 день проходит 1/10 части пути, а второй 1/15 части пути. Пусть х – количество дней, через которое они встретятся, тогда 1-й путник пройдет х*1/10, а 2-й х*1/15.

Ответ: путники встретятся через 6 дней

60+54+48= 162 (четверти) – могут смолоть все 3 жернова за сутки

81/162=1/2 (суток) – смелют все 3 жернова 81 четверть

½ *60=30 (четверт.) – смелет 1-й жернов

½*54=27(четверт.) – смелет 2-й жернов

½*48=24(четверт.) – смелет 3-й жернов

Ответ: 81 четверь жита все три жернова смелят за пол суток, 1-й жернов смелет 30 четвертей, 2-й жернов смелет 27 четвертей, 3-й жернов смелет 24 четвертей,

В один день муж выпивает1/14 кади, за 10 дней он выпивает 10/14, выходит что его жена за 10 дней выпивает 4/14 кади или 2/7.

1 (кадь)=2/7+2/7+2/7+1/7, т. е. 3 раза по 10 дней и половина 10-ти дней, т. е. 5 дней

10 + 10 +10 +5 = 35 (дней)

Ответ: жена выпьет одну кадь пития за 35 дней

1/12 кафтана — в 1 месяц

за 7 месяцев надо было заплатить 7 рублей, а дали 5.

1) 7-5=2 (руб.)=200 (коп.) — стоит недостающая часть кафтана

2) 200:5=40 (коп.) — 1/12 кафтана

3) 40х12=480 (коп.) =4 руб. 80 коп. — стоит кафтан

Ответ: кафтан стоит 4 рубля 80 копеек.

1 См. Денисов А.П., Леонтий Филиппович Магницкий (1669–1739)// М.: Просвещение. — 1967. — 143 с.

2 См. Тихонова О. Ю. Леонтий Филиппович Магницкий – математик и христианин // Научно-методический электронный журнал «Концепт». – 2016. – № 3 (март). – С. 71–75.

3 См. Арифметика Магницкого. Точное воспроизведение подлинника. С приложением статьи П. Баранова. — М.: Издание П. Баранова, 1914

4 См. Арифметика Магницкого. Точное воспроизведение подлинника. С приложением статьи П. Баранова. — М.: Издание П. Баранова, 1914.

5 См. Арифметика Магницкого. Точное воспроизведение подлинника. С приложением статьи П. Баранова. — М.: Издание П. Баранова, 1914.

Источник