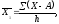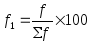- Вычисление средней арифметической по способу моментов
- 5.3 Вычисление средней арифметической способом моментов
- 5.2. Вычисление средней из вариационного ряда «способом моментов»
- Определение средней арифметической по способу моментов. Свойства средней арифметической
- Алгоритм нахождения средней по способу моментов
- Алгоритм нахождения средней по способу моментов
- Расчет средней арифметической величины способом моментов
Вычисление средней арифметической по способу моментов
При большом числе наблюдений или при большом числовом значении вариант применяют
упрощенный способ вычисления средней арифметической- способ моментов.
где М — средняя арифметическая; А — условная средняя; i — интервал между группами вариант;
S — знак суммирования.; а- условное отклонение каждой варианты от условной средней;
р — частота встречаемости вариант; n — число наблюдений.
Пример вычисления средней арифметической по способу моментов (средней массы тела
юношей в возрасте 18 лет)
| V(n в кг) | Р | а (V-А) | а . Р |
| +2 | +4 | ||
| +1 | +3 | ||
| Мо=62 | |||
| -1 | -6 | ||
| -2 | -8 | ||
| -3 | -3 | ||
| п = 25 | Sар = — 10кг |
Этапы расчета средней по способу моментов:
1) за условную среднюю А рекомендуется принять Моду или Медиану, например А = 62кг, так как 62 кг было у 9 юношей из 25;
2) определяем «а» — условное отклонение варианты от условной средней, для этого из каждой варианты вычитаем условную среднюю: а = V — А, ( например, а = 64 — 62 = +2 и т.д.).
3) умножаем условное отклонение «а» на частоту «р» каждой варианты и получаем произведение а р;
4) находим сумму Sа . р = — 10кг
5) рассчитываем среднюю арифметическую по способу моментов:
М = А + i SаР = 62 — 1×0,4 = 61,6кг
Таким образом, можно сделать вывод, что в изучаемой нами группе юношей средняя масса тела
Средняя арифметическая сама по себе ничего не говорит о том вариационном ряде, из которого
она была вычислена. На ее типичность (достоверность) влияет однородность рассматриваемого
материала и колеблемость ряда.
Пример: даны два одинаковых по числу наблюдений вариационных ряда, в которых
представлены данные измерений окружности головы детей в возрасте от 1 года до 2-х лет
| Ряд 1 | Ряд 2 | |
| Окружность головы(в см) Частота | 41, 45, 46, 47, 48 7, 8, 25, 6, 2 | 42, 43, 44, 45, 46, 47, 48, 49, 50 1, 2, 4, 6, 14, 10, 3, 0, 2 |
Имея одинаковое число наблюдений и одинаковые средние арифметические (М= 46 см), ряды
имеют различия в распределении внутри. Так варианты первого ряда отклоняются в целом от
средней арифметической с меньшим значением, чем варианты второго ряда, что дает
возможность предположить, что средняя арифметическая (46 см) более типична для первого
ряда, чем для второго.
В статистике для характеристики разнообразия вариационного ряда употребляют среднее
квадратическое отклонение (s)
Существует два способа расчета среднего квадратического отклонения: среднеарифметический
способ и способ моментов. При среднеарифметическом способе расчета применяют формулу:
где d истинное отклонение каждой варианты от истиной средней М. Формула используется при
Источник
5.3 Вычисление средней арифметической способом моментов
Способ моментов применяется для упрощения вычисления средней арифметической при условии, что варианты большие числа. Применяется в основном для рядов с равными интервалами.
1 Выбираем так называемый «ложный ноль» – это варианта, имеющая наибольшую частоту или находящаяся в середине вариационного ряда.
Замечание: в качестве «ложного ноля» можно взять и любую другую варианту, но тогда вычисления будут более сложными.
Определяем условную варианту по формуле
где А – «ложный ноль»
h – величина интервала.
3 Если частоты большие числа, то можно перевести их в проценты:
4 Вычисляем момент первого порядка по формуле
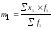
5 Вычисляем среднюю по формуле:
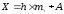
Пример 3 Вычисление средней арифметической способом моментов
Имеются следующие данные:
Группы рабочих по размеру месячной заработной платы, тыс. р.
Источник
5.2. Вычисление средней из вариационного ряда «способом моментов»
«Способ моментов» применяется в рядах с равными интервалами на основе свойств средней арифметической. Средняя арифметическая исчисляется по формуле
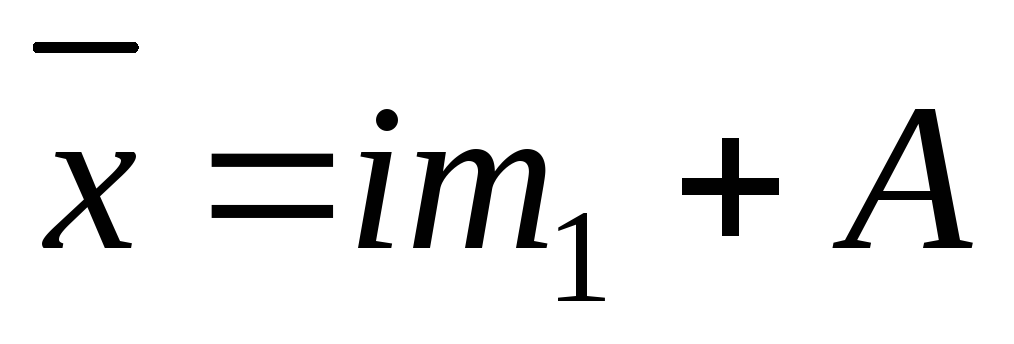
где i – размер интервала;
m1 – момент первого порядка (средняя арифметическая из новых упрощенных вариант 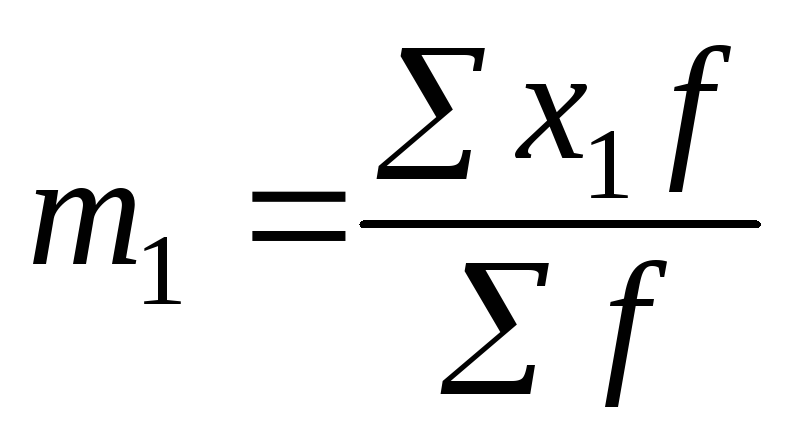
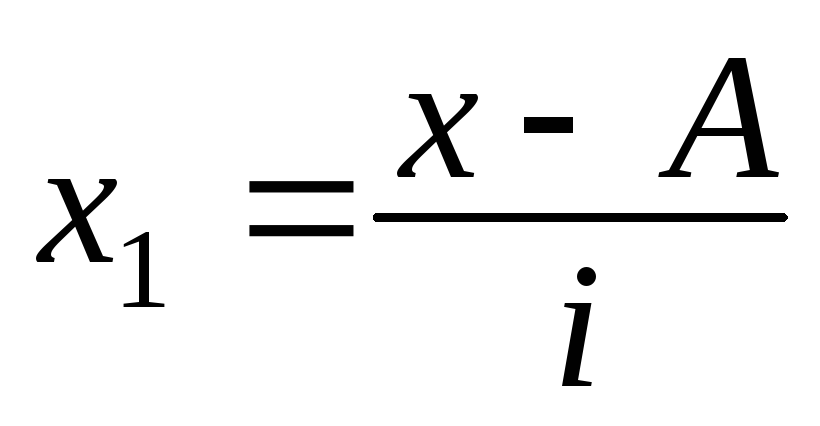
А– постоянное число (лучше всего взять его равным варианте, у которой наибольшая частота).
Определим среднее значение признака «способом моментов» на следующем примере.
Пример 5. Имеются следующие данные о распределении магазинов облпотребсоюза по торговой площади (табл. 14).
Группировка магазинов по торговой площади, м 2 (х)
Удельный вес магазинов, % ( f )
Следует определить среднюю площадь магазинов, применив «способ моментов».
Данные распределения магазинов по торговой площади представлены в виде интервального ряда распределения с равными интервалами (i = 20 м 2 ), следовательно, расчет средней площади магазина можно провести по формуле 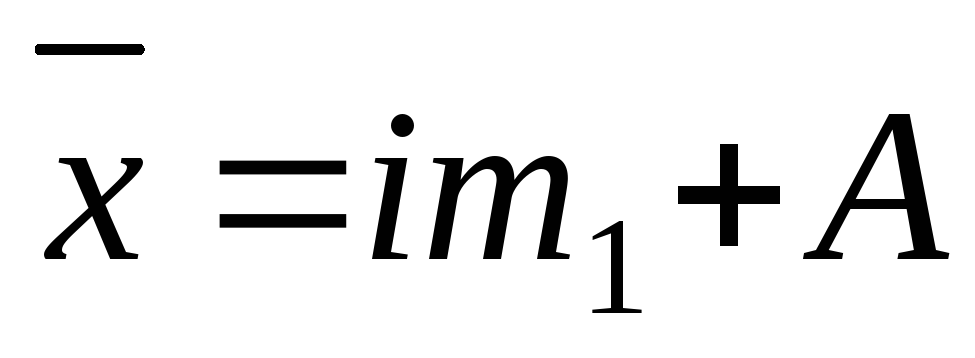
Первый и последний интервалы даны открытыми, т. е. не имеют границ нижней и верхней соответственно. Для определения среднего значения в них границы интервалов следует закрыть. Для первой группы с размером площади до 40 м 2 условно считаем, что интервал также равен 20 м 2 , затем вычитаем 20 м 2 из 40 м 2 и находим условную нижнюю границу первого интервала (20 – 40). Условную верхнюю границу последнего интервала определяем аналогично (100 – 120).
Расчеты следует проводить в табл. 15.
Группировка мага- зинов по торговой площади, м 2 (х)
Источник
Определение средней арифметической по способу моментов. Свойства средней арифметической
Где А – условный нуль, равный варианте с максимальной частотой (середина интервала с максимальной частотой), h – шаг интервала,
Назначение сервиса . С помощью онлайн-калькулятора вычисляется среднее значение по способу моментов. Результат решения оформляется в формате Word .
Инструкция . Для получения решения необходимо заполнить исходные данные и выбрать параметры отчета для оформления в Word.
Алгоритм нахождения средней по способу моментов
Пример . Затраты рабочего времени на однородную технологическую операцию распределялись между рабочими следующим образом:
Требуется определить среднюю величину затрат рабочего времени и среднеквадратическое отклонение по способу моментов; коэффициент вариации; моду и медиану.
Таблица для расчета показателей.
| Группы | Середина интервала, x i | Кол-во, f i | x i ·f i | Накопленная частота, S | (x-x ) 2 ·f |
| 5 — 10 | 7.5 | 20 | 150 | 20 | 4600.56 |
| 15 — 20 | 17.5 | 25 | 437.5 | 45 | 667.36 |
| 20 — 25 | 22.5 | 50 | 1125 | 95 | 1.39 |
| 25 — 30 | 27.5 | 30 | 825 | 125 | 700.83 |
| 30 — 35 | 32.5 | 15 | 487.5 | 140 | 1450.42 |
| 35 — 40 | 37.5 | 10 | 375 | 150 | 2200.28 |
| 150 | 3400 | 9620.83 |
Мода
где x 0 – начало модального интервала; h – величина интервала; f 2 –частота, соответствующая модальному интервалу; f 1 – предмодальная частота; f 3 – послемодальная частота.
Выбираем в качестве начала интервала 20, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 22.78 мин.
Медиана
Медианным является интервал 20 — 25, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
Таким образом, 50% единиц совокупности будут меньше по величине 23 мин.
.
Находим А = 22.5, шаг интервала h = 5.
Средний квадрат отклонений по способу моментов . 
| x ц | x * i | x * i f i | 2 f i |
| 7.5 | -3 | -60 | 180 |
| 17.5 | -1 | -25 | 25 |
| 22.5 | 0 | 0 | 0 |
| 27.5 | 1 | 30 | 30 |
| 32.5 | 2 | 30 | 60 |
| 37.5 | 3 | 30 | 90 |
| 5 | 385 |

Среднее квадратическое отклонение .
мин.
Коэффициент вариации — мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Поскольку v>30% ,но v . С помощью онлайн-калькулятора вычисляется среднее значение по способу моментов. Результат решения оформляется в формате Word .
Инструкция . Для получения решения необходимо заполнить исходные данные и выбрать параметры отчета для оформления в Word.
Алгоритм нахождения средней по способу моментов
Пример . Затраты рабочего времени на однородную технологическую операцию распределялись между рабочими следующим образом:
Требуется определить среднюю величину затрат рабочего времени и среднеквадратическое отклонение по способу моментов; коэффициент вариации; моду и медиану.
Таблица для расчета показателей.
| Группы | Середина интервала, x i | Кол-во, f i | x i ·f i | Накопленная частота, S | (x-x ) 2 ·f |
| 5 — 10 | 7.5 | 20 | 150 | 20 | 4600.56 |
| 15 — 20 | 17.5 | 25 | 437.5 | 45 | 667.36 |
| 20 — 25 | 22.5 | 50 | 1125 | 95 | 1.39 |
| 25 — 30 | 27.5 | 30 | 825 | 125 | 700.83 |
| 30 — 35 | 32.5 | 15 | 487.5 | 140 | 1450.42 |
| 35 — 40 | 37.5 | 10 | 375 | 150 | 2200.28 |
| 150 | 3400 | 9620.83 |
Мода
где x 0 – начало модального интервала; h – величина интервала; f 2 –частота, соответствующая модальному интервалу; f 1 – предмодальная частота; f 3 – послемодальная частота.
Выбираем в качестве начала интервала 20, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 22.78 мин.
Медиана
Медианным является интервал 20 — 25, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).
Таким образом, 50% единиц совокупности будут меньше по величине 23 мин.
.
Источник
Расчет средней арифметической величины способом моментов



Этот способ расчета средней арифметической величины основан на использовании ее математических свойств. Среднюю арифметическую величину вычисляют по формуле
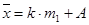
где 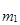
k – величина равного интервала или любое постоянное число, отличное от нуля;
А – любое постоянное число.
Момент 1-го порядка вычисляют по формуле
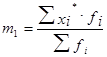
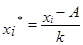
Пример 3. По исходным данным примера 2 вычислить средний размер премии одного работника способом моментов.
Решение. Пусть А = 6 000 и k = 500. Расчеты представлены в таблице:
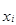 | 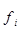 | 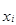 | 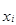 – 6000 – 6000 | 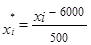 | 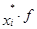 |
| 3 000–5 000 | 4 000 | – 2 000 | – 4 | – 16 | |
| 5 000– 7000 | 6 000 | ||||
| 7 000–10 000 | 8 500 | 2 500 | |||
| 10 000–15 000 | 12 500 | 6 500 | |||
| Итого |
Вычислим момент первого порядка
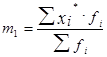
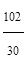
Средний размер заработной платы одного работника составил
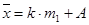
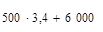
Источник