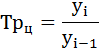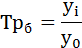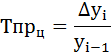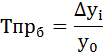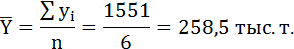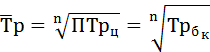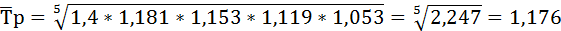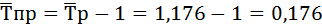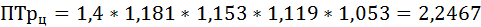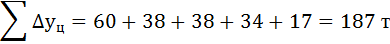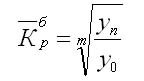Средний темп прироста базисным способом

Задача №56. Расчёт аналитических показателей динамики

Добыча нефти характеризуется следующими данными:

Годы	Добыча нефти, тыс. т
1-ый	150
2-ой	210
3-ий	248
4-ый	286
5-ый	320
6-ой	337

Произвести анализ ряда динамики по:

1) показателям, характеризующим рост добычи нефти (на цепной и базисной основе): абсолютный прирост, темпы роста и прироста (по годам к базисному году); результаты расчетов изложить в табличной форме;

2) средний уровень и среднегодовой темп ряда динамики;

3) показать взаимосвязь между цепными и базисными показателями.

Решение:

Абсолютный прирост цепной (Δy_ц) – это разность между текущим уровнем ряда и предыдущим:

Так, во 2-ом г. прирост добычи нефти в сравнении с первым годом составит:

= 210 – 150 = 60 тыс. т.

В 3-ем году прирост добычи нефти в сравнении со 2-м годом составит:

Δy_{ц 3-й год} = 248 – 210 = 38 тыс. т.

Аналогично исчисляются абсолютные приросты за последующие годы. Результаты расчётов занесём в таблицу.

Абсолютный прирост базисный (Δy_б) – это разность между текущим уровнем ряда и уровнем ряда, выбранным за базу сравнения:

Так как в задании не указано, какой год взять в качестве базисного года, по умолчанию будем считать базисным 1-й год.

Абсолютный прирост базисный во 2-ом г. совпадает с цепным абсолютным приростом в этом году:

Δy_б = 210 – 150 = 60 тыс. т

в 3-ем году базисный абсолютный прирост равен:

Δy_б = y₃ – y₂ = 248 – 150 = 98 тыс. т и т.д (гр. 3 расчётной таблицы).

Темп роста (Тр) – отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.

Цепной темп роста исчисляют отношением текущего уровня к предыдущему:

(гр. 5 расчётной таблицы);

базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения:

(гр. 4 расчётной таблицы).

Темп прироста (Тпр) так же может быть цепной или базисный.

Цепной рассчитывается как отношение абсолютного прироста к предыдущему уровню ряда динамики:

Базисный темп прироста рассчитывается как отношение абсолютного прироста к базисному уровню ряда динамики:

Если предварительно был вычислен темп роста, то темп прироста можно рассчитать как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах:

или как разность между темпами роста и 100%, если темпы роста выражены в процентах:

Тпр= Тр – 100% (гр. 6 и 7 расчётной таблицы).

Годы	Добыча нефти, тыс. т	Абсолютный прирост базисный, тыс. т	Абсолютный прирост цепной, тыс. т	Темп роста базисный, %	Темп роста цепной, %	Темп прироста базисный, %	Темп прироста цепной, %
А	1	2	3	4	5	6	7
1-ый	150	0	—	100,00	—	—	—
2-ой	210	60	60	140,00	140,0	40,00	40,0
3-ий	248	98	38	165,33	118,1	65,33	18,1
4-ый	286	136	38	190,67	115,3	90,67	15,3
5-ый	320	170	34	213,33	111,9	113,33	11,9
6-ой	337	187	17	224,67	105,3	124,67	5,3

Из таблицы видно, что добыча нефти росла от года к году. Однако прирост добычи с каждым годом становился меньше.

2) Средний уровень ряда определяется в данном случае по формуле средней арифметической простой, где в числителе сумма уровней динамического ряда, а в знаменателе их число:

Среднегодовой темп роста ряда динамики рассчитывается по формуле средней геометрической

где ПТр – произведение цепных темпов роста (в коэффициентах),

– конечный базисный темп роста (в коэффициентах),

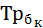
n – число темпов.

Среднегодовой темп прироста ряда динамики:

Добыча нефти ежегодно возрастала в среднем на 17,6%.

3) Между цепными и базисными темпами роста имеется взаимосвязь:

произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста.

Сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту:

Выводы: С 1 по 6 годы добыча нефти росла от года к году. Объём добычи нефти за эти годы вырос на 124,7%, что в абсолютном выражении составило 187 т. Однако ежегодный прирост добычи с каждым годом снижался. В среднем добыча нефти ежегодно возрастала на 17,6%.

Источник

СПИСОК ЛИТЕРАТУРЫ ОНЛАЙН

Как рассчитать темп роста и прироста?

Темп роста — это прирост какой-либо изучаемой величины за один временной период (обычно применяется к году).

Темп прироста — это прирост какой либо изучаемой величины за один временной период за вычетом 100%.

Темп роста и темп прироста измеряются в процентах и являются относительными величинами. Темп роста — всегда величина положительная, темп прироста может быть отрицательным. Темп прироста равен темп роста минус 100%.

Теперь рассмотрим расчет темпа роста и темпа прироста более подробно.

Расчет темпа роста и прироста

Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: темп роста и темп прироста. Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов — формулы расчета темпа роста и прироста.

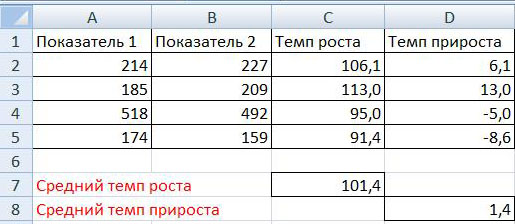
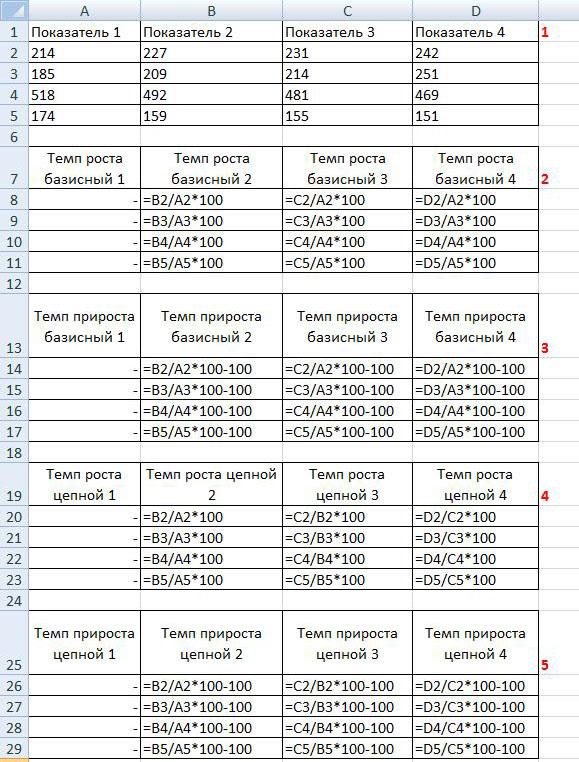
На рисунке представлен пример расчета темпа роста и прироста:

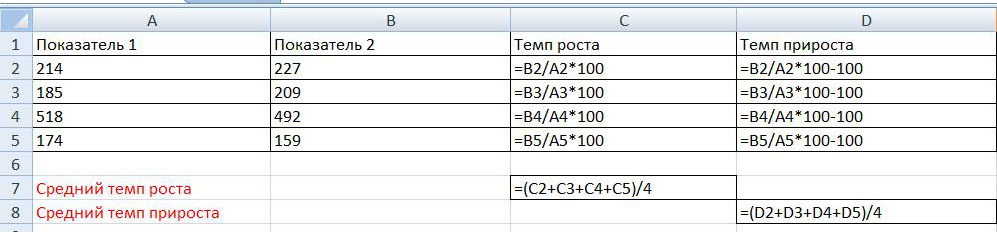
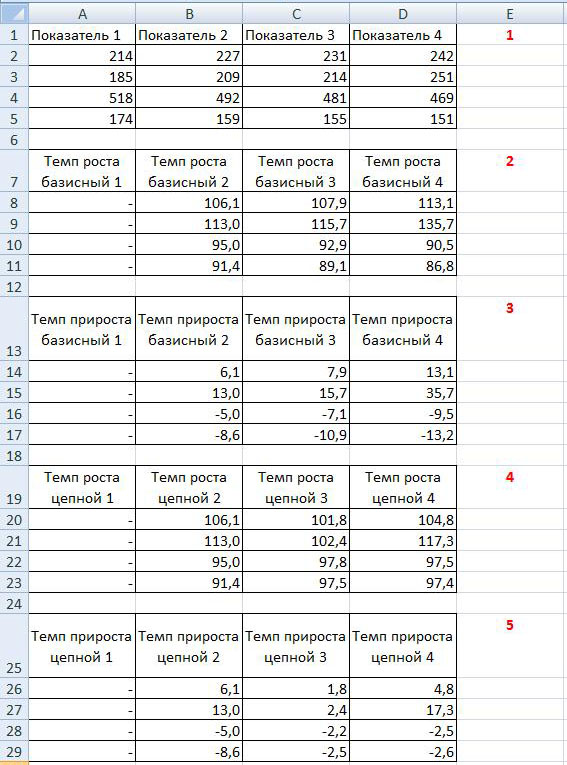
Для наглядности на рисунке ниже приведен этот же пример, только с открытыми формулами:

На рисунке видно, что определение темпа роста осуществляется путем деления Показателя 2 на Показатель 1 и умножения на 100%. При этом темп прироста равен: деление показателя 2 на показатель 1 умножение на 100% и минус 100%, то есть темп прироста равен темп роста минус 100%.

Расчет средних темпов роста и прироста

Так же на рисунках указано как рассчитывается средний темп роста и средний темп прироста. Для определения среднего темпа роста необходимо сложить показатели за все четыре периоды и разделить полученную сумму на количество периодов, то есть на 4. Аналогично рассчитывается средний темп прироста — сумма темпов прироста за все периоды делится на количество периодов.

Расчет базисного темпа роста и базисного темпа прироста

Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста. Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов — формулы расчета темпа роста и прироста.

На рисунке ниже представлен расчет базисного темпа роста и прироста (таблицы 2 и 3):

Расчет базисного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей. Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя.

В примере за базисный показатель принят Показатель 1, поэтому базисный темп роста или базисный темп прироста рассчитывается исходя из этого положения, то есть при расчете базисного темпа роста Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, при расчете базисного темпа прироста из каждого показателя базисного темпа роста вычитаем 100.

Расчет цепного темпа роста и цепного темпа прироста

На рисунке выше представлен расчет базисного темпа роста и прироста (таблицы 4 и 5).

Расчет цепного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей. Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя. В отличие от базисного темпа роста или прироста, цепной темп роста или прироста рассчитывается из текущего и предыдущего показателя.

То есть цепной темп роста или цепной темп прироста рассчитывается следующим образом: Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 2 и умножаем на 100, далее Показатель 4 делим на Показатель 3 и умножаем на 100, при расчете цепного темпа прироста из каждого показателя цепного темпа роста вычитаем 100.

Для того, чтобы закрепить полученную информацию, обратите внимание на рисунок ниже, в котором отражены формулы расчета: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста:

Обратите внимание, что при расчете базисного и цепного показателей, значения базисного и цепного темпов роста и прироста равны, так как при избрании в качестве базисного показателя первого из ряда, они рассчитываются одинаково.

Источник

Средние показатели динамики: уровень ряда, абсолютный прирост, темп роста

Средний уровень ряда в статистике

Средний уровень ряда определяет обобщенную величину абсолютных уровней. Он определяется по средней, исчисленной из значений, меняющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики разные.

Средний уровень из абсолютных уровней для интервальных рядов динамики рассчитывается по формуле средней арифметической:

1. При равных интервалах используют среднюю арифметическую простую:

где у — абсолютные уровни ряда;

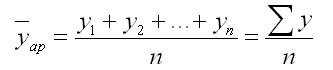
n — число уровней ряда.

2. При неравных интервалах используют среднюю арифметическую взвешенную:

где у1,…,уn — уровни ряда динамики;

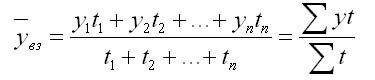
t1,… tn — веса, длительность интервалов времени.

Средний уровень моментного ряда динамики рассчитывается по формуле:

1. С равностоящими уровнями рассчитывается по формуле средней хронологической моментного ряда:

где у1,…,уn — уровни периода, за который делается расчет;
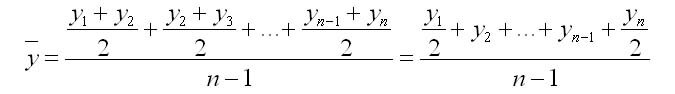
n — число уровней;
n-1 — длительность периода времени.

2. С неравностоящими уровнями рассчитывается по формуле средней хронологической взвешенной:

где у1,…,уn — уровни рядов динамики;
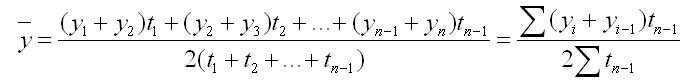
t — интервал времени между смежными уровнями

Средний абсолютный прирост в задачах статистики

Средний абсолютный прирост определяется как среднее из абсолютных приростов за равные промежутки времени одного периода. Он рассчитывается по формулам:

1. По цепным данным об абсолютных приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую:

где n — число степенных абсолютных приростов в исследуемом периоде.

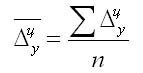
2. Средний абсолютный прирост рассчитывают через базисный абсолютный прирост в случае равных интервалов

где m — число уровней ряда динамики в исследуемом периоде, включая базисный.

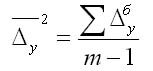
Средний темп роста

Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.

В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую.

Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»:

где n — число цепных коэффициентов роста;
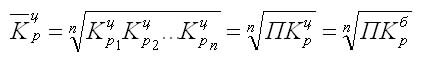
Кц — цепные коэффициенты роста;
Кб — базисный коэффициент роста за весь период.

Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста.

Формула для определения среднего коэффициента роста для равностоящих рядов динамики по «базисному способу» будет такая:

Средний темп прироста

Средние темпы прироста рассчитываются на основе средних темпов роста (Тр) вычитанием из последних 100%:

Для того чтобы определить средний коэффициент прироста (Кпр), нужно из значений коэффициентов роста (Кр) вычесть единицу.

Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.

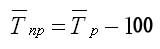
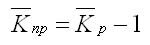
Источник