Сравнение треугольников способом наложения

Знакомство с треугольником
план-конспект занятия по математике (младшая группа)

Программное содержание: Познакомить с треугольником: учить различать и называть фигуру. Совершенствовать умение сравнивать две равные группы предметов способом наложения, обозначать результаты сравнения словами много, поровну, столько — сколько. Закреплять навыки сравнения двух предметов по ширине, учить пользоваться словами широкий — узкий, шире — уже, одинаковые по ширине. Развивать логическое мышление у детей, наблюдательность, умение сопоставлять, сравнивать.

Воспитывать интерес к математике, дружеские взаимоотношения с детьми.

Скачать:

Вложение	Размер
f3.docx	19.34 КБ

Предварительный просмотр:

ФЭМП Знакомство с треугольником

Программное содержание : Познакомить с треугольником : учить различать и называть фигуру. Совершенствовать умение сравнивать две равные группы предметов способом наложения, обозначать результаты сравнения словами много, поровну, столько — сколько. Закреплять навыки сравнения двух предметов по ширине, учить пользоваться словами широкий — узкий, шире — уже, одинаковые по ширине. Развивать логическое мышление у детей, наблюдательность, умение сопоставлять, сравнивать.

Воспитывать интерес к математике, дружеские взаимоотношения с детьми.

I.Введение в игровую ситуацию

Воспитатель : Ребята, посмотрите, кто к нам пришел? К нам пришел зайчик.

Зайчик здоровается с детьми.

Воспитатель : Зайчик, ты почему такой грустный. (Зайчик протягивает конверт.)

Зайчик : Здесь какие-то фигуры, а я не знаю, как они называются.

Воспитатель : Не огорчайся, Зайка, ребята тебе расскажут, что это за фигуры. Правда, дети? (Да.)

II.Основной этап занятия.

1.В письме геометрические фигуры : круг и треугольник . Воспитатель достает круг:

— Что нам принес зайчик?

— Какого цвета круг?

Воспитатель предлагает обвести круг пальчиком.

Затем достает треугольник и кладет рядом с кругом :

— Что нам еще принес зайчик? Кто знает, как называется эта фигура?

— Это треугольник . Какого цвета треугольник ?

— Что есть у треугольника ?

— Дети : Стороны, углы

-. Сколько сторон (углов)?

Воспитатель предлагает детям хором вместе с ним посчитать углы и повторить название фигуры.

Воспитатель обобщает ответы и действия детей.

2 .Малышарики. Умные песенки. Треугольник. https://www.youtube.com/watch?time_continue=80&v=b_MRFWzytRs&feature=emb_logo

3.Открытие нового знания

(дети сидят за столами)

Игровое упражнение «Найди такую же» .

Перед детьми на столе разложены геометрические фигуры — круг и треугольник .

Зайчик по очереди «показывает» фигуры, дети находят у себя такие же и называют их.

Затем воспитатель предлагает обвести фигуры рукой и наложить круг на треугольник так , чтобы углы треугольника были видны . Дети выясняют, чем треугольник отличается от круга .

4. Физминутка «Зайка»

Зайка серенький сидит

И ушами шевелит.

Вот так, вот так,

И ушами шевелит.

Зайке холодно сидеть,

Надо лапочки погреть.

Вот так, вот так.

Надо лапочки погреть.

Надоело зайке спать,

Надо зайке поскакать.

Вот так, вот так,

Надо зайке поскакать.

5.Игровое упражнение «Достроим домики для зайчиков» .

— Ребята, смотрите, наш Зайчик опять загрустил. Что случилось, Зайка?

Зайка : У моих зайчат нет домиков.

— Не расстраивайся, Зайчик мы поможем тебе построить домики.

Воспитатель : Ребята, посмотрите. А ведь у нас с вами есть домики!

— Сколько у нас домиков?

— Чего не хватает у домиков?

— Какую фигуру надо взять, чтобы сделать домику крышу?

Воспитатель : У вас есть треугольники? Сколько у вас треугольников?

Воспитатель : Положите свои треугольники на домики.

— Сколько получилось крыш?

— Что можно сказать о количестве крыш и наложенных треугольников ?»

— Дети : Домов и крыш поровну.

— Домов столько сколько и крыш.

— Ребята, сколько крыш и домов? (Воспитатель добивается вариативных ответов для обозначения равенства предметов.)

(широкая, узкая дорожка на паласе)

6. Игровое упражнение «Перепрыгнем через ледяную дорожку» .

— Ребята, чтобы зайчатам добраться до домиков им необходимо помочь перепрыгнуть через ледяные дорожки.

На полу — две «ледяные» дорожки. Воспитатель предлагает детям сравнить их по ширине, показать широкую (узкую) дорожку. Одинаковые ли по ширине дорожки? (Да.) Затем ребята по очереди перепрыгивают через дорожки. Воспитатель выясняет : «Через какую дорожку — широкую или узкую — вы прыгнули дальше?»

Зайчик благодарит детей за помощь и прощается. (Дети прощаются с Зайчиком.)

— Ребята, вы молодцы!

— С какой фигурой мы познакомились ?

— Сколько домиков, крыш?

— Через что мы перепрыгивали? Какой ширины дорожки?

По теме: методические разработки, презентации и конспекты

НОД «Знакомство с треугольником»

Интеграция образовательных областей «Познание», «Коммуникация», «Художественное творчество», «Социализация». Способ организации детей на занятии: с подгруппой детей.Цель: познакомить с геом.

Презентация «Знакомство с ТРЕУГОЛЬНИКОМ»

1. Вспоминаем известные фигуры: — КРУГ: Нет углов у меня И похож на блюдце я, На медаль, на блинок, На осиновый листок. Людям я старинный друг. Называют меня … — КВАДРАТ Что пох.

Конспект непрерывной образовательной деятельности «Знакомство с треугольником» (вторая младшая группа)

Конспект непосредственной оразовательной деятельности по формированию элементарных математических представлений для детей младшего возраста.

Знакомство с треугольником, на основе сравнения его с квадратом.

Формирование умения сравнивать и различать геометрические фигуры по одному из признаков.

Конспект НОД по ФЭМП во второй младшей группе «Знакомство с треугольником».

Конспект НОД по ФЭМП во второй младшей группе «Знакомство с треугольником».

План-конспект открытого занятия по формированию элементарных математических представлений Тема: «Знакомство с треугольником».

1. Познакомить с новой геометрической фигурой – треугольником, формировать умение различать и называть фигуру, обследовать форму осязательно-двигательным путём.2. Совершенствовать умение с.

Конспект занятия по математике в младшей группе «Знакомство с треугольником. Сравнение двух предметов по ширине и двух равных групп предметов по количеству».

Конспект занятия по математике в младшей группе.Тема: «Знакомство с треугольником. Сравнение двух предметов по ширине и двух равных групп предметов по количеству».

Источник

Признаки равенства треугольников

О чем эта статья:

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

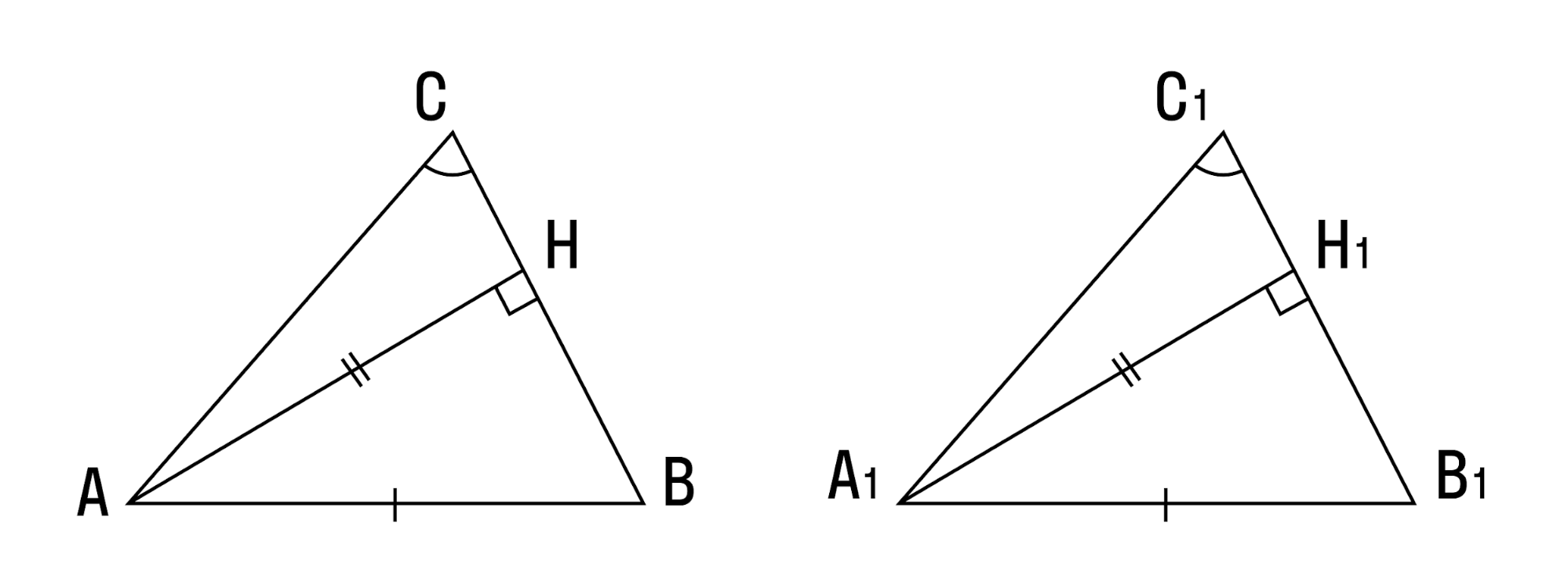
1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
   
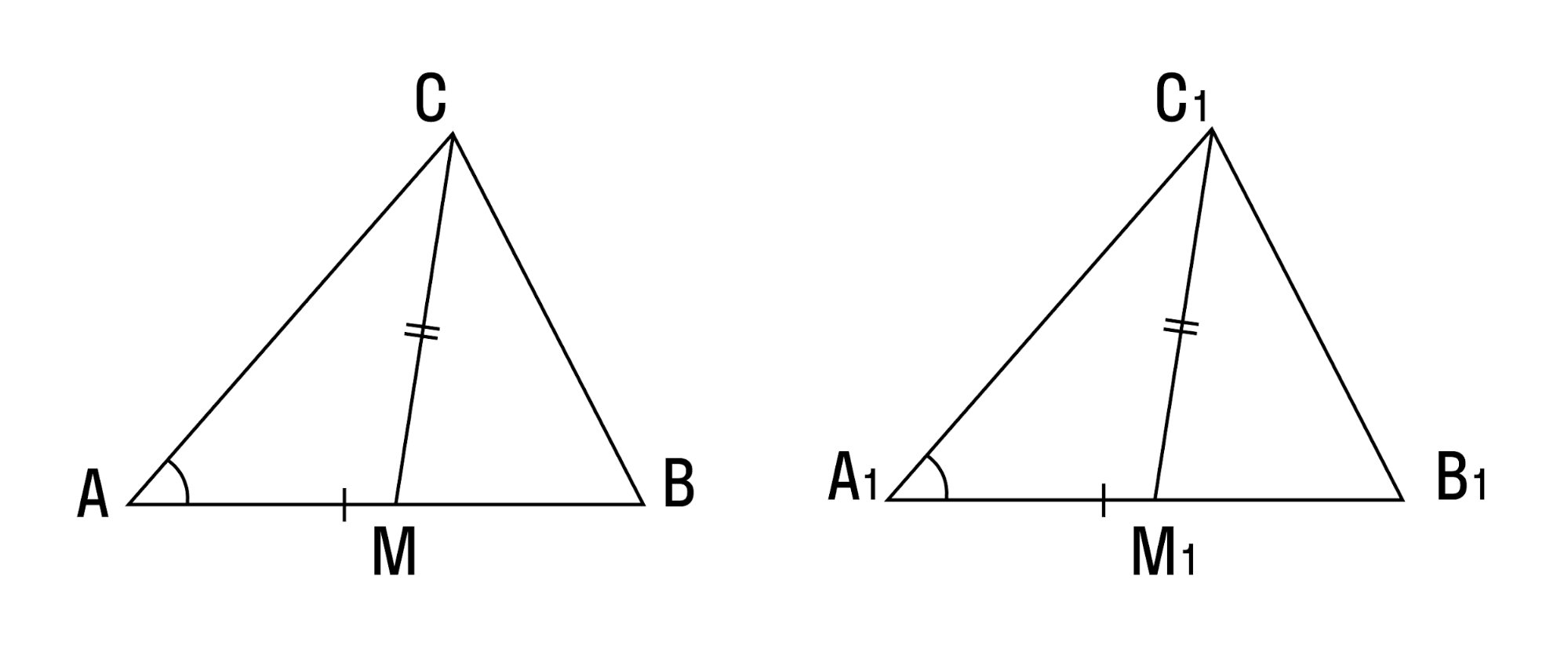
2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
   
3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
   
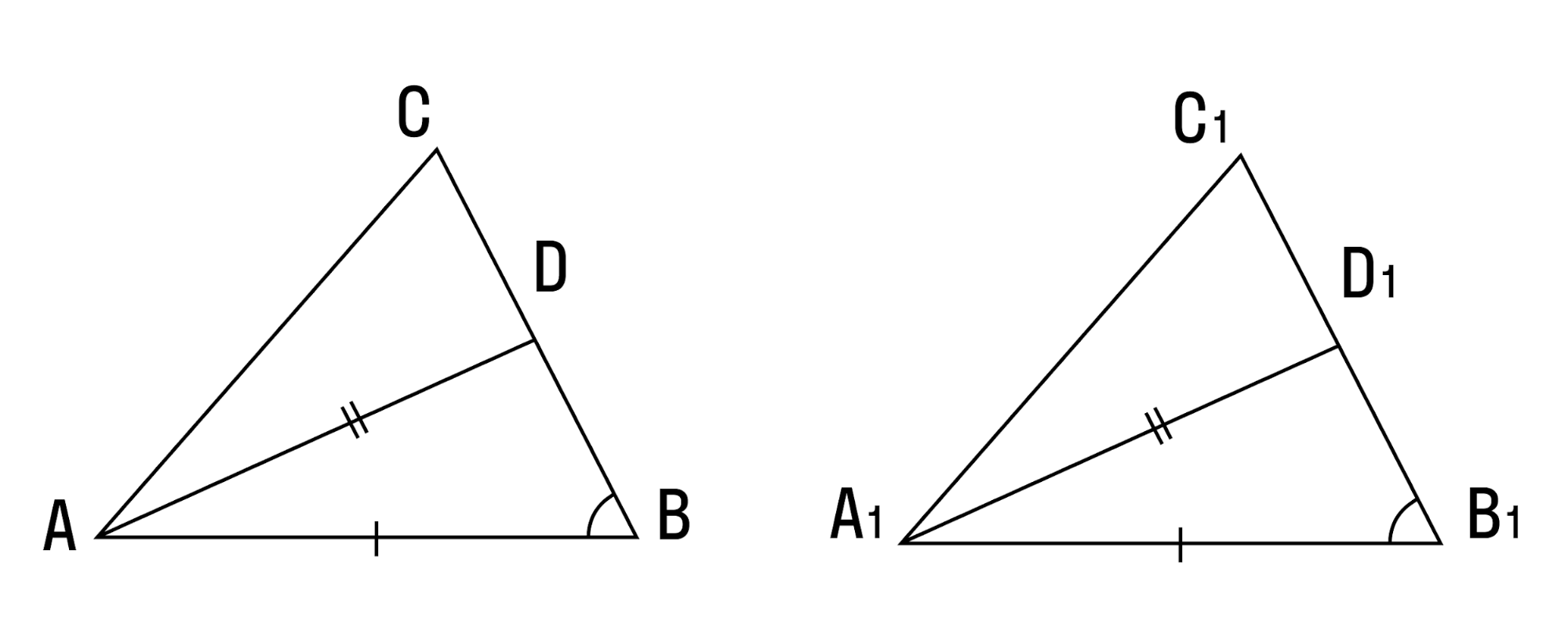
4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
   
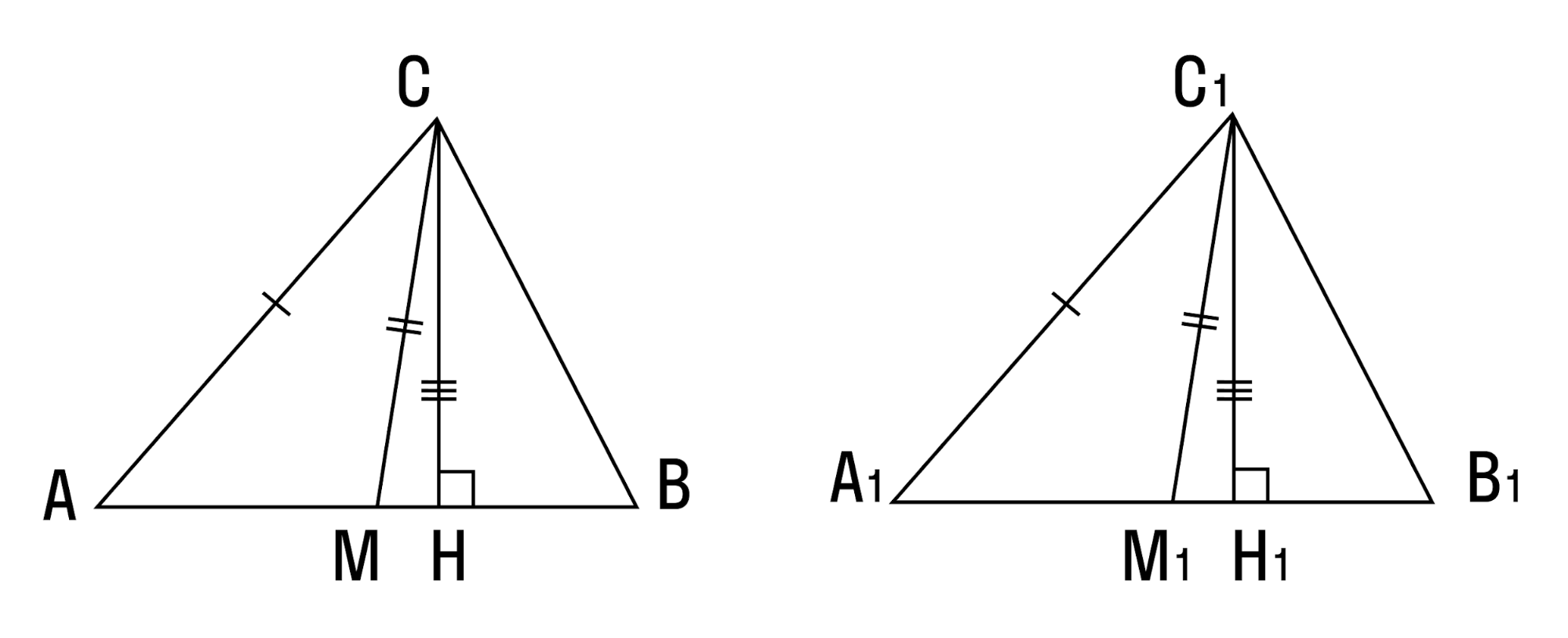
5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
   

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Источник

Геометрия. 7 класс

Конспект урока

Первый признак равенства треугольников

Перечень рассматриваемых вопросов:

• Равные треугольники.
• Первый признак равенства треугольников.
• Решение задач с применением теоремы о равенстве треугольников.

Стороны треугольника– отрезки, соединяющие вершины треугольника

Равные треугольники – треугольники,которые можно совместить наложением.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

2. Погорелов А. В. Геометрия: 7–9 класс. // Погорелов А. В. – М.: Просвещение, 2017. – 224 с.

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Мы уже познакомились со способом сравнения треугольников путем наложения. Например, поворачивая треугольники, построенные Фалесом, на 180°, мы совмещали стороны и углы.

Но бывают ситуации, в которых этот способ неприменим. Например, если возникает необходимость сравнивать земельные участки треугольной формы.

Сегодня мы узнаем, как можно установить равенство треугольников без наложения их друг на друга.

Мы познакомились со способом определения расстояния до недоступной точки, предложенным Фалесом. Этот способ примечателен не только своей новизной по меркам древней Греции, но и тем, что Фалес впервые в истории науки понял необходимость доказательства.

Сравнить треугольники можно используя, так называемые, признаки равенства треугольников.

Чтобы убедиться в равенстве треугольников способом наложения, необходимо проверить равенство 6 соответственных элементов: 3 сторон и 3 углов треугольников.

Оказывается, что все 6 проверять нет необходимости. Мы сегодня докажем, что достаточно проверить только 3 пары элементов.

Будем утверждать, что достаточно сравнить только 3 пары элементов – 2 стороны и угол между ними.

В математике любое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой.

А сами рассуждения называются доказательством теоремы.

Рассмотрим теорему о равенстве треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Формулировка теоремы состоит из двух частей. Первая часть начинается словом «если». В ней говорится о том, что дано. Это часть называется условием теоремы.

Вторая часть теоремы начинается словом «то». В ней говорится о том, что надо доказать. Вторая часть формулировки теоремы называется её заключением.

Дано: ∆ ABC, ∆А₁В₁С₁, АВ = А₁В₁, АС = А₁С₁, А =А₁.

вершина А совместится с вершиной А₁, стороны АВ и АС наложатся соответственно на лучи А1В1 и А₁С₁.

В частности, совместятся точки В и В_1, С и С₁. Сторона ВС совпадет со стороной В₁С_1.

Доказанная теорема позволит нам сделать вывод о равенстве треугольников, сравнивая 3 пары элементов – по 2 сторонам и углу между ними каждого треугольника.

Такая теорема называется признаком.

В частности, первым признаком равенства треугольников.

Разбор заданий тренировочного модуля.

Доказать, что треугольники АВD и АСD равны.

Рассмотрим ∆ROS и ∆РОТ:

Из равенства треугольников следует, что ∠Т =∠R (как соответствующие элементы равных треугольников). Значит, ∠Т = 30°.

Докажите, что центрально симметричные отрезки равны.

Доказательство: Точки А и В являются центрально симметричными относительно точки О, если они лежат на одной прямой , проходящей через центр О, на равных расстояниях от центра О.

Добавим еще одну пару центрально симметричных точек относительно точки О – точки С и D.

Соединим отрезками точки А и С, В и D. Получим отрезки АС и ВD, которые являются центрально симметричными относительно точки О.

Докажем, что отрезки АС и ВD равны.

Рассмотрим треугольники АОС и ВОD:

Из равенства треугольников следует равенство соответственных элементов, т.е. АС = ВD.

Таким образом, мы доказали равенство центрально симметричных отрезков.

Источник