Способы заполнения пропущенных значений

К сожалению, на практике в ходе сбора данных далеко не всегда удается полностью укомплектовать исходные таблицы. Пропуски отдельных значений являются повсеместным явлением и поэтому, прежде чем начать применять статистические методы, обрабатываемые данные следует привести к “каноническому” виду. Для этого необходимо либо удалить фрагменты объектов с недостающими элементами, либо заменить имеющиеся пропуски на некоторые разумные значения.

Проблема “борьбы с пропусками” столь же сложна, как и сама статистика, поскольку в этой области существует впечатляющее множество подходов. В русскоязычных книгах по использованию R (Кабаков, 2014; Мастицкий, Шитиков, 2015) бегло представлены только некоторые функции пакета mice, который, несмотря на свою “продвинутость”, мало удобен для практической работы с данными умеренного и большого объема. Хорошей альтернативой являются методы «knnImpute» , «bagImpute» и «medianImpute» функции preProcess() из пакета caret , которую мы рассмотрели в разделе 3.3 как инструмент для трансформации данных.

Используем в качестве примера для дальнейших упражнений таблицу algae , включенную в пакет DMwR и содержащую данные гидробиологических исследований обилия водорослей в различных реках. Каждое из 200 наблюдений содержит информацию о 18 переменных, в том числе:

три номинальных переменных, описывающих размеры size = c(«large», «medium», «small») и скорость течения реки speed = c(«high», «low», «medium») , а также время года season = c(«autumn», «spring», «summer», «winter») , сопряженное с моментом взятия проб;
8 переменных, составляющих комплекс наблюдаемых гидрохимических показателей: максимальное значение рН mxPH (1), минимальное содержание кислорода mnO2 (2), хлориды Cl (10), нитраты NO3 (2), ионы аммония NH4 (2), орто-фосфаты oPO4 (2), общий минеральный фосфор PO4 (2) и количество хлорофилла а Chla (12) (в скобках приведено число пропущенных значений);
средняя численность каждой из 7 групп водорослей a1 — a7 (видовой состав не идентифицировался).

Читатель может самостоятельно воспользоваться функциями описательной статистики summary() или describe() из пакета Hmisc , а мы постараемся поддержать добрую традицию и привести парочку примеров диаграмм, построенных с использованием пакета ggplot2 (рис. 3.4):

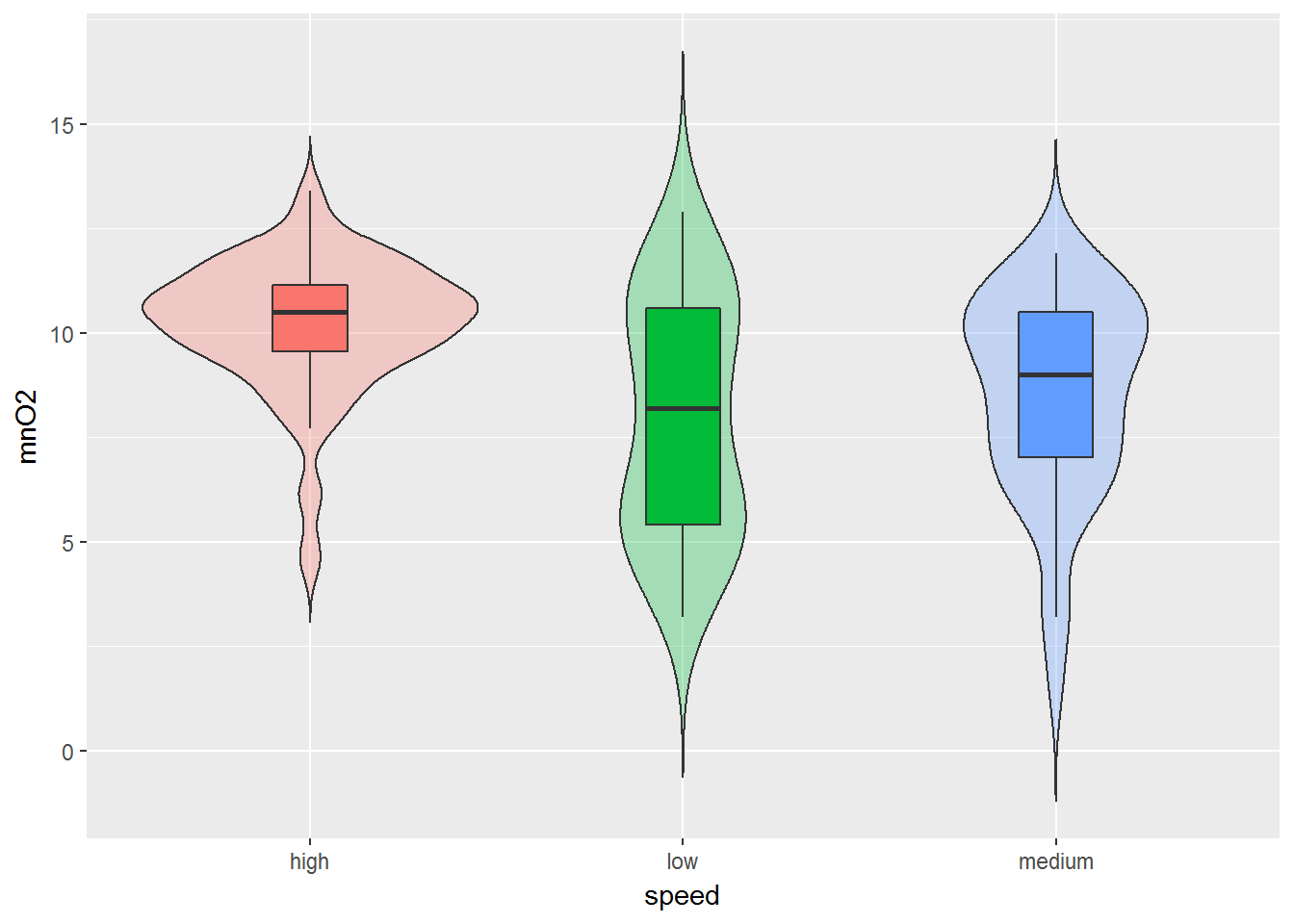
Рисунок 3.4: Распределения значений содержания кислорода в воде рек с разной скоростью течения

На рис. 3.4 мы получили так называемую “скрипичную диаграмму” (violin plot), которая объединяет в себе идеи диаграмм размахов и кривых распределения вероятности. Суть достаточно проста: продольные края “ящиков с усами” (для сравнения приведены тоже) замещаются кривыми плотности вероятности. В итоге, например, легко можно выяснить не только тот факт, что в потоках с быстрым течением (high) содержание кислорода выше, но и ознакомиться с характером распределения соответствующих значений.

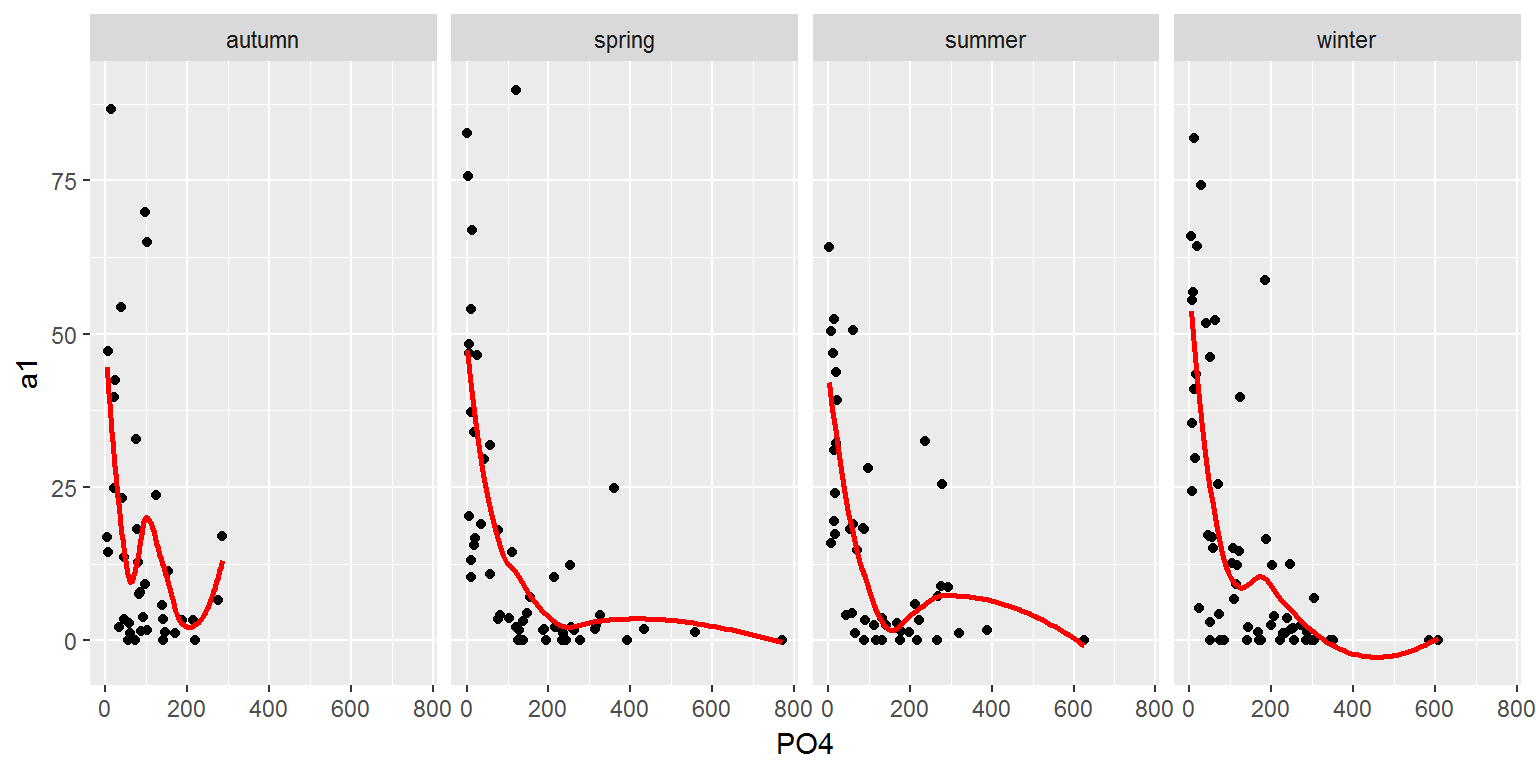
Другой пример — категоризованные графики, удобные для визуализации данных, разбитых на отдельные подмножества (категории), каждое из которых отображается в отдельной диаграмме подходящего типа. Такие диаграммы, или “панели” (от англ. panels, facets или multiples), определенным образом упорядочиваются и размещаются на одной странице. Из графиков, представленных на рис. 3.5, легко увидеть, что численность водорослей группы а1 падает с увеличением концентрации фосфатов.

Рисунок 3.5: Графики изменения обилия водорослей в зависимости от содержания минерального фосфора в разное время года

Однако в контексте темы этого раздела важно обратить внимание на то, что мы все время старались блокировать появление пропущенных значений: algae[!is.na(algae$PO4), ] . Если в обрабатываемой таблице обнаружены недостающие данные, то в общих чертах можно избрать одну из следующих возможных стратегий:

удалить строки с неопределенностями;
заполнить неизвестные значения выборочными статистиками соответствующей переменной (среднее, медиана и т.д.), полагая, что взаимосвязь между переменными в имеющемся наборе данных отсутствует (это соответствует известному “наивному” подходу);
заполнить неизвестные значения с учетом корреляции между переменными или меры близости между наблюдениями; постараться обходить эту неприятную ситуацию, используя, например, формальный параметр na.rm некоторых функций.

Последняя альтернатива является наиболее ограничивающей, поскольку она далеко не во всех случаях позволяет осуществить необходимый анализ. В свою очередь, удаление целых строк данных слишком радикально и может привести к серьезным потерям важной информации:

Можно удалить не все строки, а только те, в которых число пропущенных значений превышает, например, 20% от общего числа переменных, для чего существует специальная функция из пакета DMwR :

В результате мы удалили только две строки (62-ю и 199-ю), где число пропущенных значений больше одного. Обратите внимание, что выполняя команду data(algae) , мы каждый раз обновляем в памяти содержимое этого набора данных.

Если мы готовы принять гипотезу о том, что зависимостей между переменными нет, то простым и часто весьма эффективным способом заполнения пропусков является использование средних значений. В том случае, если есть сомнения в нормальности распределения данных, предпочтительнее использовать медиану. Покажем, как это можно сделать с использованием функции preProcess() из пакета caret :

Альтернативой “наивному” подходу является учет структуры связей между переменными. Например, можно воспользоваться тем, что между двумя формами фосфора oPO4 и PO4 существует тесная корреляционная связь. Тогда, например, можно избавиться от некоторых неопределенностей в показателе PO4 , вычислив его пропущенные значения по уравнению простой регрессии:

Одно из пропущенных значений удалось восстановить.

Разумеется, легко придти к мысли не утруждать себя перебором всех возможных корреляций, а учесть все связи одновременно и целиком. Использование метода «bagImpute» осуществляет для каждой из имеющихся переменных построение множественной бутстреп-агрегированной модели, или бэггинг-модели (bagging), на основе деревьев регрессии, используя все остальные переменные в качестве предикторов. Этот метод мудр и точен, но требует значительных затрат времени на вычисление, особенно при работе с данными большого объема:

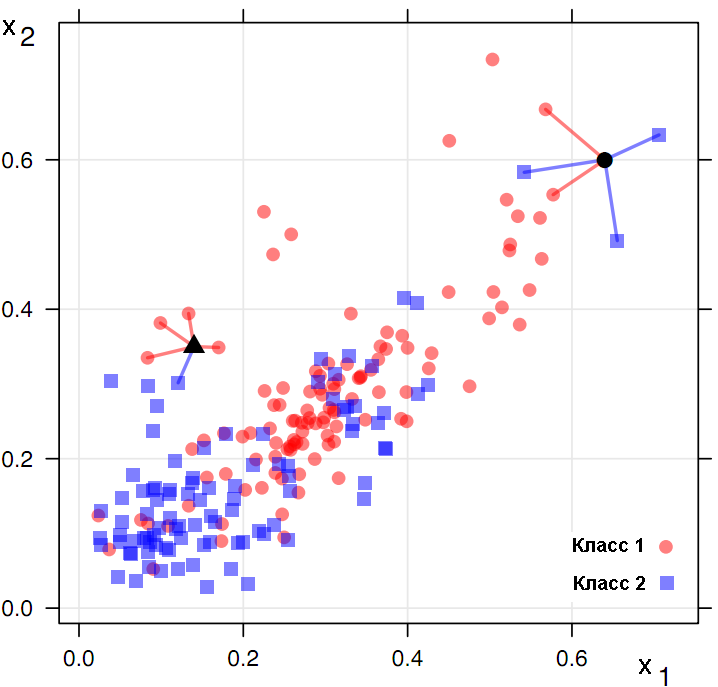
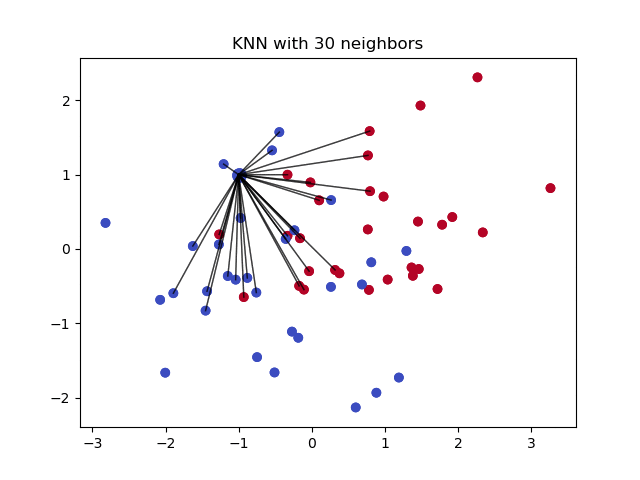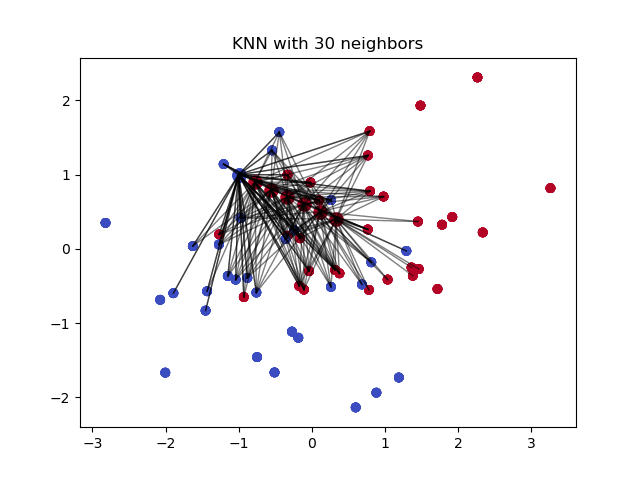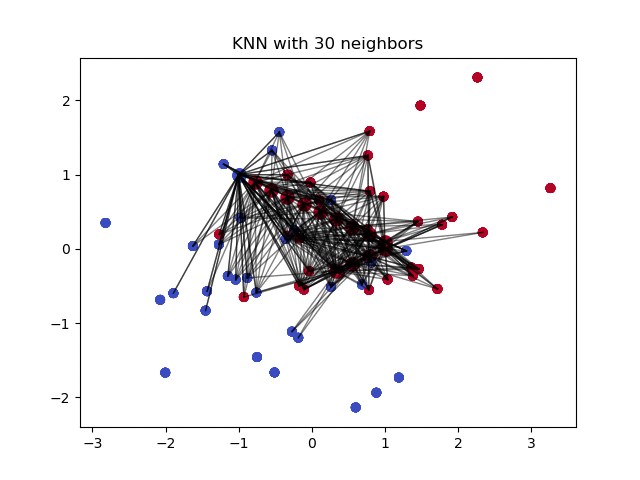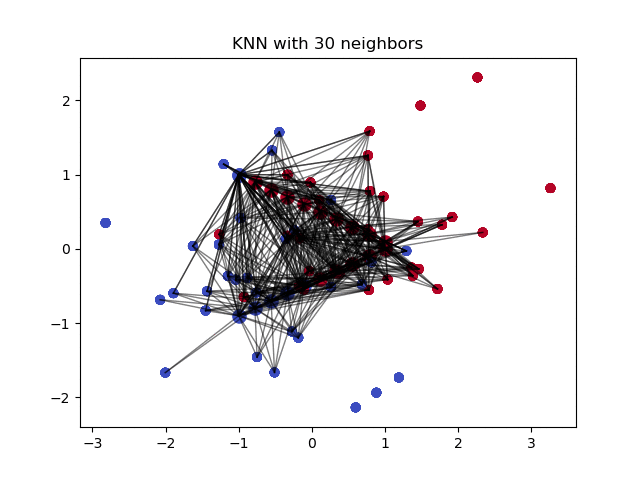
Наконец, третий метод функции preProcess() для заполнения пропусков — «knnImpute» — основан на простейшем, но чрезвычайно эффективном алгоритме k ближайших соседей (k-nearest neighbours) или kNN. В основе метода kNN лежит гипотеза о том, что тестируемый объект d будет иметь примерно тот же набор признаков, что и обучающие объекты в локальной области его ближайшего окружения (рис. 3.6).

Рисунок 3.6: Интерпретация метода k ближайших соседей

Если речь идет о классификации, то неизвестный класс объекта определяется голосованием $k$ его ближайших соседей (на рис. 3.6 $k = 5$ ). kNN-регрессия оценивает значение неизвестной координаты $Y$ , усредняя известные ее величины для тех же $k$ соседних точек.

Одна из важных проблем kNN — выбор метрики, на основе которой оценивается близость объектов. Наиболее общей формулой для подсчета расстояния в m-мерном пространстве между объектами $\mathbf$ и $\mathbf$ является мера Минковского: \[ D_S (\mathbf, \mathbf) = (\sum |x_ <1i>— x_<2i>|^p )^<1>,\]

где $i$ изменяется от 1 до $m$ , а $r$ и $p$ — задаваемые исследователем параметры, с помощью которых можно осуществить нелинейное масштабирование расстояний между объектами. Мера расстояния по Евклиду получается, если принять в метрике Минковского $r = p = 2$ , и является, по-видимому, наиболее общей мерой расстояния, знакомой всем со школы по теореме Пифагора. При $r = p = 1$ имеем “манхеттенское расстояние” (или “расстояние городских кварталов”), не столь контрастно оценивающее большие разности координат $x$ . Вторая проблема метода kNN заключается в решении вопроса о том, на мнение какого числа соседей $k$ нам целесообразно положиться? В свое время мы обсудим этот вопрос детально, а сейчас будем ориентироваться на значение $k = 5$ , используемое по умолчанию:

Получив в результате применения predict() матрицу переменных с пропущенными значениями, заполненными этим методом, мы с удивлением обнаруживаем, что данные оказались стандартизованными (т.е. центрированными и нормированными на стандартное отклонение). Но а как иначе можно было вычислить меру близости по переменным, измеренным в разных шкалах? Пришлось для возвращения в исходное состояние применить обратную операцию:

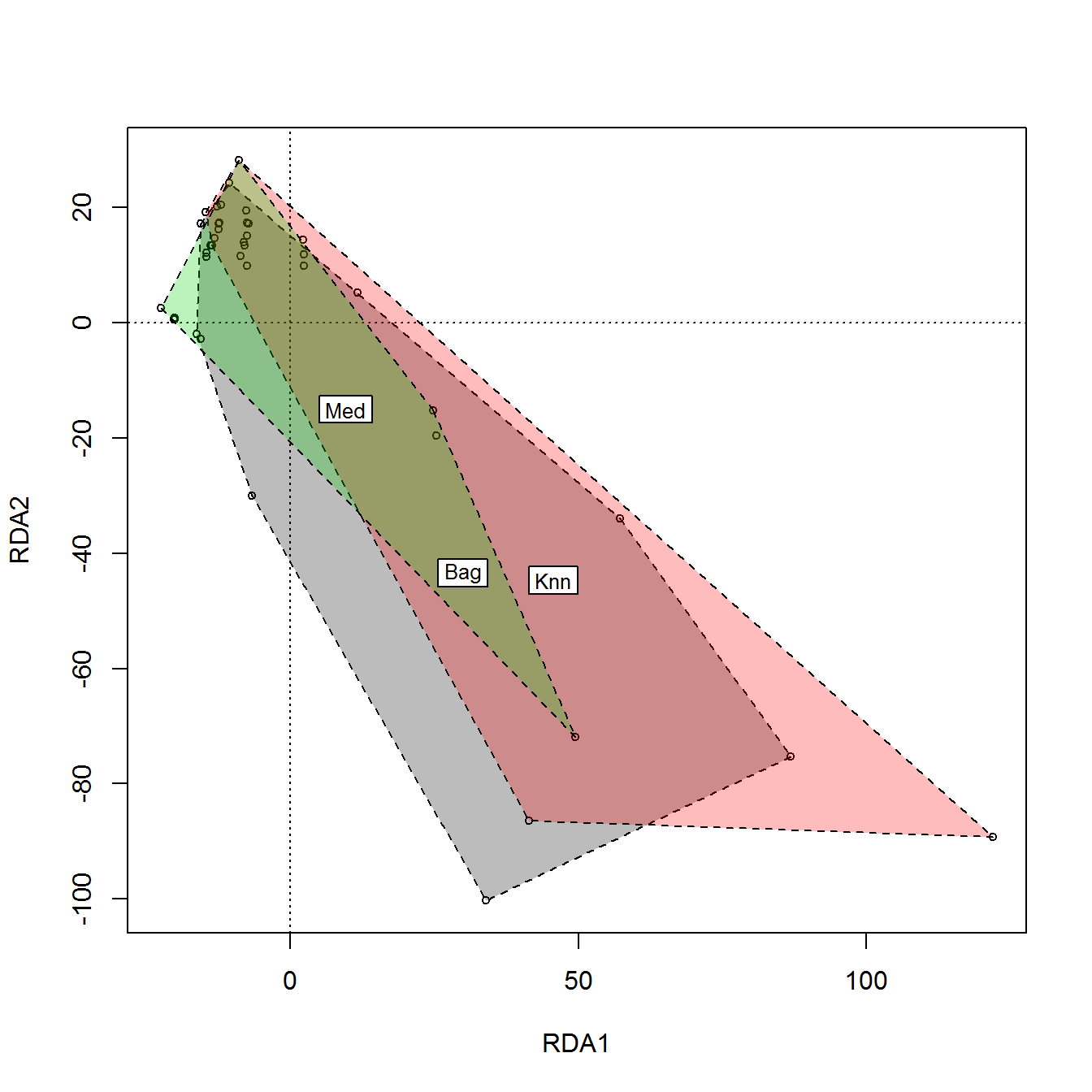
Наконец, зададимся следующим закономерным вопросом: а какой метод лучше? Обычно эта проблема не имеет теоретического решения, и исследователь полагается на собственную интуицию и опыт. Но мы можем оценить, насколько расходятся между собой результаты, полученные каждым способом заполнения. Для этого сформируем блок данных из $3 \times 16 = 48$ строк исходной таблицы с пропусками, заполненными тремя методами ( «Med» , «Bag» , «Knn» ), и выполним снижение размерности пространства переменных методом главных компонент в двумерное (см. раздел 2.4). Посмотрим, как “лягут карты” на плоскости (рис. 3.7):

Рисунок 3.7: Ординационная диаграмма блоков данных таблицы algae с пропущенными значениями, заполненными разными способами

На рис. 3.7 мы выделили контуром (hull), проведенным через крайние точки, области каждого из трех блоков данных и поместили метку метода в центры тяжести полученных многоугольников. Понятно, что медианное заполнение характеризуется меньшей вариацией результатов, поскольку игнорирует специфичность свойств каждого объекта. Оба других метода, учитывающих внутреннюю структуру данных, дали приблизительно похожие результаты.

Источник

Что делать, если в датасете пропущены данные? — 6 способов импутации данных с примерами

Авторизуйтесь

Что делать, если в датасете пропущены данные? — 6 способов импутации данных с примерами

Автор перевода Алексей Морозов

Реальные наборы данных могут быть неполными. Не в том смысле, что в анализ не вошли какие-то важные точки или неудачно были выбраны параметры, а просто отсутствуют некоторые данные, которые в принципе должны были там быть.

Это может случиться из-за технических проблем, или если датасет собран из нескольких источников с разными наборами параметров; важно то, что в таблице присутствуют пустые ячейки. Вместо значений в них ставится какая-нибудь заглушка — NaN, просто пустая ячейка или ещё что-нибудь в этом роде. Если их много — тренировка на таких данных сильно ухудшит качество модели, а то и окажется вовсе невозможной. Многие алгоритмы того же scikit-learn не только требуют массив чисел (а не NaN или «missing»), но и ожидают, что этот массив будет состоять из валидных данных.

Что делать? Можно, конечно, просто выкинуть все неполные наблюдения, но так можно потерять ценную информацию. Лучше попытаться восстановить недостающие значения на основании остальных данных в наборе, или хотя бы вставить в пустые ячейки что-нибудь более-менее осмысленное. Этот процесс называется импутацией данных.

3–4 декабря, Онлайн, Беcплатно

В этой статье будет описано 6 популярных способов импутации для наборов однородных точек. Для временных серий они непригодны, там всё делается совсем иначе.

Способ первый: не делать ничего

Тут всё просто: отдаём алгоритму датасет в исходном виде и надеемся, что он с ним как-нибудь разберётся. Некоторые алгоритмы умеют принимать во внимание и даже восстанавливать пропущенные значения в данных. Например, XGBoost делает это за счёт уменьшения функции потерь при обучении. У алгоритма может быть параметр, позволяющий их проигнорировать (пример — LightGBM с параметром use_missing=False ). Но таких опций может и не быть: линейная регрессия в scikit-learn просто объявит массив некорректным и выбросит исключение. Так что в её случае (как и в случае многих других алгоритмов) готовить данные к анализу всё-таки придётся пользователю.

Плюсы:

Не надо думать об алгоритмах импутации — выставил соответствующие параметры и всё работает.

Минусы

Нужно понимать, как именно алгоритм обойдётся с недостающими данными. В противном случае есть риск получить какие-нибудь артефакты и даже не узнать, какие именно.

Способ второй: импутация данных средним/медианой

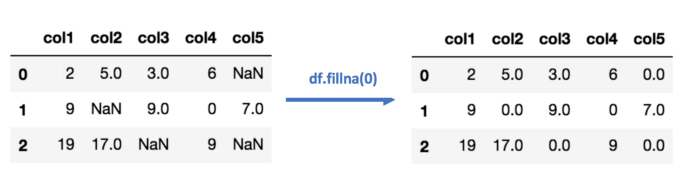
Тоже не особенно сложно: считаем среднее или медиану имеющихся значений для каждого столбца в таблице и вставляем то, что получилось, в пустые ячейки. Естественно, этот метод работает только с численными данными.

В коде это выглядит примерно так:

Плюсы:

Просто и быстро.
Хорошо работает на небольших наборах численных данных.

Минусы:

Значения вычисляются независимо для каждого столбца, так что корреляции между параметрами не учитываются.
Не работает с качественными переменными.
Метод не особенно точный.
Никак не оценивается погрешность импутации.

Способ третий: импутация данных самым частым значением или константой

Импутация самым часто встречающимся значением — ещё одна простая стратегия для компенсации пропущенных значений, не учитывающая корреляций между параметрами. Плюсы и минусы те же, что и в предыдущем пункте, но этот метод предназначен для качественных переменных.

В случае импутации нулём или константой (как можно догадаться из названия) все пропущенные значения в данных заменяются определённым значением.

Способ четвёртый: импутация данных с помощью k-NN

k-Nearest Neighbour (k ближайших соседей) — простой алгоритм классификации, который можно модифицировать для импутации недостающих значений. Он использует сходство точек, чтобы предсказать недостающие значения на основании k ближайших точек, у которых это значение есть. Иными словами, выбирается k точек, которые больше всего похожи на рассматриваемую, и уже на их основании выбирается значение для пустой ячейки. Это можно сделать с помощью библиотеки Impyute:

Алгоритм сперва проводит импутацию простым средним, потом на основании получившегося набора данных строит дерево и использует его для поиска ближайших соседей. Взвешенное среднее их значений и вставляется в исходный набор данных вместо недостающего.

Плюсы:

На некоторых датасетах может быть точнее среднего/медианы или константы.
Учитывает корреляцию между параметрами.

Минусы:

Вычислительно дороже, так как требует держать весь набор данных в памяти.
Важно понимать, какая метрика дистанции используется для поиска соседей. Имплементация в impyute поддерживает только манхэттенскую и евклидову дистанцию, так что анализ соотношений (скажем, количества входов на сайты людей разных возрастов) может потребовать предварительной нормализации.
Чувствителен к выбросам в данных (в отличие от SVM).

Способ пятый: импутация данных с помощью MICE

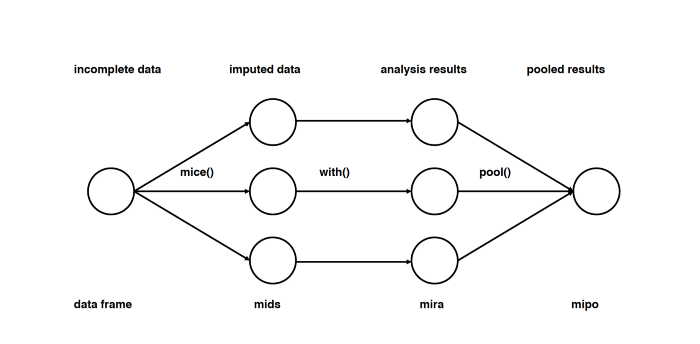
Этот подход основан на том, что импутация каждого значения проводится не один раз, а много. Множественные импутации, в отличие от однократных, позволяют понять, насколько надёжно или ненадёжно предложенное значение. Кроме того, MICE позволяет работать с переменными разных типов (например двоичными и количественными), а также со сложными штуками вроде предельных значений и паттернов артефактов в исходных данных. Подробный разбор математики есть в оригинальной статье.

Прим. пер. Судя по статье, метод MICE подразумевает не просто множественные импутации, а многократное повторение дальнейшего анализа на разных импутированных наборах данных и интеграцию получившихся результатов.

Способ шестой: импутация данных с помощью глубокого обучения

Показано, что глубокое обучение хорошо работает с дискретными и другими не-численными значениями. Библиотека datawig позволяет восстанавливать недостающие значения за счёт тренировки нейросети на тех точках, для которых есть все параметры. Поддерживается тренировка на CPU и GPU.

Плюсы:

Точнее других методов.
Может работать с качественными параметрами.
Поддерживает CPU и GPU.

Минусы:

Восстанавливает только один столбец.
На больших наборах данных может быть вычислительно дорого.
Нужно заранее решить, какие столбцы будут использоваться для предсказания недостающего значения.

Другие методы импутации данных

Стохастическая регрессия

Примерно похоже на регрессионную импутацию, в которой значения восстанавливаются регрессией от имеющихся значений для той же точки, но добавляет случайный шум.

Экстраполяция и интерполяция

Пытается восстановить значения на основании ограниченного набора известных точек.

Hot-deck

Значение берётся из другой точки, похожей по имеющимся параметрам на восстанавливаемую. Грубо говоря, это похоже на k-NN, но используется только один «сосед».

Как мы видим, универсального метода импутации не существует. Одни стратегии работают лучше на одних наборах данных или типах недостающих переменных, другие на других. Если не считать очевидных правил насчёт типов данных (например, у качественных переменных просто не может быть среднего), то можно только посоветовать экспериментировать и смотреть, какой метод сработает лучше на данном конкретном датасете.

Источник