Способы замены плоскостей способ параллельного перемещения

Способы замены плоскостей способ параллельного перемещения

Контрольные задания по теме: Рабочая тетрадь задача 50

Трудоемкость и точность графического решения задач часто зависит не только от сложности задач, но и от того, какое положение занимают геометрические фигуры по отношению к плоскостям проекций. Наиболее выгодными являются положения, параллельные плоскостям проекций или перпендикулярные им.

Переход от общего положения геометрической фигуры к частному можно осуществить двумя путями:

а) перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения;

б) выбором новой плоскости проекций, по отношению к которой фигура, не имеющая своего положения в пространстве, окажется в частном положении. Первый путь лежит в основе способа плоскопараллельного перемещения, а второй — в основе способа замены плоскостей проекций.

Существует несколько способов плоскопараллельного перемещения:

1. Способ параллельного перемещения. При этом плоскости, по которым двигаются точки фигуры, параллельны плоскости проекций. Траектория — произвольная плоская линия;

2. Способ вращения вокруг оси, перпендикулярной к плоскости проекций. Траектории перемещаемых точек — дуги окружностей, центры которых находятся на оси вращения;

3. Способ вращения вокруг оси параллельной плоскости проекций (вокруг линии уровня).

Это частный случай параллельного перемещения. За траекторию движения точки принимается не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между осью вращения и данной точкой.

При вращении точки вокруг оси перпендикулярной, П 2 , фронтальная проекция точки перемещается по окружности, а горизонтальная — по прямой, перпендикулярной оси вращения. Если же точка вращается вокруг оси, перпендикулярной П 1 , то в горизонтальной плоскости траекторией ее движения будет окружность, а во фронтальной – прямая, перпендикулярная оси вращения. На рисунке 32 показано построение новых проекций точек при помощи способа вращения. На рисунке 32 а – вращение вокруг фронтально-проецирующей оси, на рисунке 32 б – вокруг горизонтально-проецирующей оси.

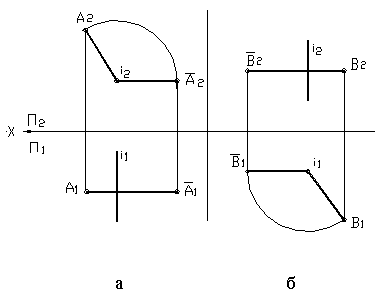
Рисунок 32

Этим способом удобно находить натуральные величины отрезков и фигур, занимающих проецирующее положение.

На рисунке 33 показан пример определения натуральной величины треугольника АВС, плоскость которого перпендикулярна П 2 . За ось вращения необходимо взять фронтально-проецирующую прямую, проходящую через точку, принадлежащую этой плоскости. В данном случае выбрана точка А — вершина треугольника. Плоскость треугольника вращается во фронтальной плоскости вокруг оси до положения, параллельного горизонтальной плоскости. Во фронтальной плоскости точки С и В перемещаются по окружностям, радиус которых равен расстоянию от оси вращения до фронтальных проекций точек. В горизонтальной плоскости траектории движения точек – прямые, перпендикулярные оси. Полученная проекция треугольника А´В´С´, является его натуральной величиной.

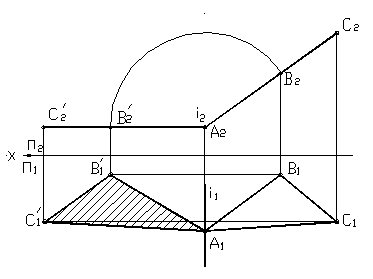
Рисунок 33

Способ вращения наиболее часто применяется при определении натуральных величин сечений поверхностей плоскостями частного положения.

Сущность этого способа состоит в том, что положение фигуры в пространстве не меняется, а вводится новая система плоскостей проекций. Новая плоскость проекции выбирается перпендикулярно к одной из старых. При этом, проецируемая фигура по отношению к новой плоскости занимает частное положение, обеспечивая наиболее удобное решение задачи. Если замена одной плоскости не обеспечивает требуемый результат, то новую плоскость заменяют еще раз.

На рисунке 34 показано построение проекции точки А в новой системе плоскостей проекций при замене плоскости П 1 на П 4 . Плоскость П 4 перпендикулярна П 2 . Проекция точки А1 заменяется на А 4 . По линии связи откладывается расстояние от заменяемой проекции точки до новой оси.

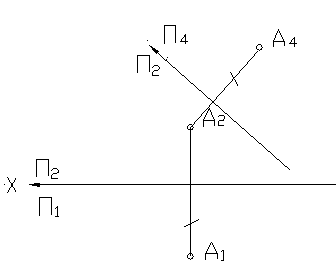
Рисунок 34

На рисунке 35 дан пример определения натуральной величины отрезка общего положения. Новая плоскость П 4 выбирается параллельно одной из проекций отрезка. При этом проекция отрезка на эту плоскость будет являться его натуральной величиной.

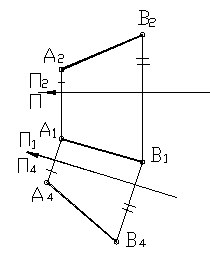
Рисунок 35

В некоторых случаях требуется замена двух плоскостей проекции. Например, при определении расстояния от точки до прямой. При этом прямую необходимо спроецировать в точку. На рисунке 36 отрезок общего положения переведен в проецирующее положение по отношению к плоскости П₅.

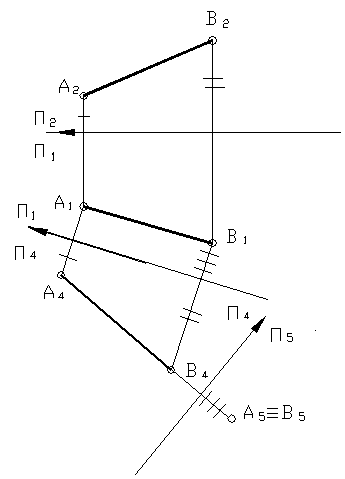
Рисунок 36

1. Назовите, какие вы знаете способы преобразования чертежа. Для чего они применяются?

2. Какие задачи можно решать при помощи способа вращения вокруг проецирующей оси?

3. По каким линиям перемещаются проекции точки при вращении вокруг горизонтально проецирующей оси?

4. Можно ли определить натуральную величину фигуры общего положения способом вращения вокруг проецирующей оси?

5. В чем суть способа замены плоскостей проекций?

6. Как построить проекцию точки в новой системе плоскостей проекций? Этапы построения.

7. Сколько замен нужно осуществить, чтобы перевести отрезок общего положения в проецирующее положение?

8. Как нужно выбрать новую плоскость, для того, чтобы сделать плоскость общего положения проецирующей?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Метод плоскопараллельного перемещения

В начертательной геометрии метод плоскопараллельного перемещения используется, как правило, для определения натуральных величин плоских фигур, отрезков и углов.

Свойства плоскопараллельного перемещения:

1. При перемещении любой фигуры параллельно плоскости проекции, проекция фигуры на эту плоскость остается неизменной.
2. При перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. На рисунке ниже точки C» и D», следуя этому свойству, заняли положение C»₁ и D»₁.
3. При перемещении точки параллельно фронтальной плоскости проекции, её горизонтальная проекция движется по прямой, параллельной оси X.

Рассмотрим перевод произвольно расположенного отрезка CD в положение, параллельное горизонтальной плоскости проекций П₂.

• Используя первое свойство параллельного перемещения, на любом свободном месте чертежа строим отрезок C’₁D’₁ = C’D’.
• По линиям связи определяем недостающие проекции C»₁ и D»₁. Стрелками показано перемещение точек C» и D» параллельно оси X в соответствии со вторым свойством рассматриваемого метода.

Следующий рисунок иллюстрирует перевод отрезка MN в проецирующее положение по отношению к фронтальной плоскости проекций П₂. В общем случае для решения подобной задачи необходимо дважды воспользоваться методом плоскопараллельного перемещения.

• После первого преобразования отрезок MN займет положение параллельно плоскости П₁. Сначала строится M»₁N»₁ = M»N» на произвольном месте чертежа, после чего по линиям связи находятся недостающие проекции M’₁ и N’₁.
• Второе преобразование заключается в параллельном переносе горизонтальной проекции отрезка M’₁N’₁ в положение M’₂N’₂, перпендикулярное оси X. После этого точки M»₂ = N»₂ определяются по линиям связи.

Определение натуральной величины треугольника

Рассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.

1. Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
2. Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим C’₁D’₁ = C’D’ перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения достраиваем треугольник A’₁B’₁C’₁ = A’B’C’. По линиям связи определяем точки A»₁, B»₁, C»₁.
3. Перемещаем проекцию A»₁B»₁C»₁ треугольника ABC в положение A»₂B»₂C»₂, параллельное оси X, соблюдая равенство A»₂B»₂C»₂ = A»₁B»₁C»₁. По линиям связи определяем точки A’₂, B’₂, C’₂. Теперь треугольник ABC расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину A’₂B’₂C’₂.

Определение расстояния между параллельными прямыми

Расстояние между двумя параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки первой прямой на вторую прямую. Рассмотрим, как указанное расстояние определяется на практике с помощью метода плоскопараллельного перемещения.

Путем двух последовательных преобразований прямые a и b переводятся в положение, перпендикулярное горизонтальной плоскости. Таким образом, они проецируются на неё в точки A’₂ и B’₂, расстояние между которыми является искомым. Показанные на рисунке величины d₁ и d₂ являются вспомогательными для выполнения построений согласно свойствам плоскопараллельного перемещения.

Источник

Метод замены плоскостей проекций

Для решения целого ряда задач начертательной геометрии наиболее рациональным является метод замены плоскостей проекций. Например, с его помощью можно определить натуральную величину плоской фигуры, расстояние между параллельными прямыми, опорные точки пересечения поверхностей.

Замена одной плоскости проекции

Сущность метода заключается в замене одной из плоскостей проекций на дополнительную плоскость, выбранную так, чтобы в новой системе плоскостей решение поставленной задачи значительно упрощалось. Положение фигур в пространстве при этом не меняется.

Рассмотрим на примере точек A и B, как осуществляются построения на комплексном чертеже. Изначально точка A находится в системе плоскостей П₁, П₂. Введем дополнительную горизонтальную пл. П₄. Она будет перпендикулярна фронтальной плоскости проекций П₂ и пересечет её по оси x₁. Эту ось необходимо провести на комплексном чертеже с учётом цели построения. Здесь мы расположили её произвольно.

В новой системе плоскостей положение точки A» не изменится. Чтобы найти точку A’₁, которая является проекцией т. А на плоскость П₄, проведем из A» перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок A_x1А’₁, равный отрезку A_xA’.

Данные построения основаны на равенстве ординат точек A’ и А’₁. Действительно, в системе плоскостей П₁, П₂ и в системе П₂, П₄ точка A удалена от фронтальной плоскости проекций П₂ на одно и то же расстояние.

Теперь осуществим перевод точки B в новую систему плоскостей П₁, П₄ (рис. ниже). Для этого введем произвольную фронтальную пл. П₄, которая будет перпендикулярна горизонтальной плоскости проекций П₁ и пересечет её по оси x₁.

В системе П₁, П₄ положение точки B’ останется неизменным. Чтобы найти точку B»₁, проведем из B’ перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок B_x1B»₁ равный отрезку B_xB». Описанные построения основаны на равенстве аппликат точек B» и B»₁.

Замена двух плоскостей проекций

Иногда для решения поставленной задачи требуется замена двух плоскостей проекций (рис. ниже). Пусть A’ и A» – исходные проекции точки A, находящейся в системе пл. П₁, П₂. Введем первую дополнительную плоскость П₄ и определим новую горизонтальную проекцию A’₁ точки A, как это было описано ранее.

Для осуществления второй замены плоскости проекций будем рассматривать систему пл. П₂, П₄ в качестве исходной. Введем новую фронтальную плоскость П₅ перпендикулярно горизонтальной пл. П₄. Для этого на произвольном месте чертежа проведем ось x₂ = П₄ ∩ П₅. Из точки A’₁, положение которой останется неизменным, восстановим перпендикуляр к оси x₂. На нем от точки A_x2 отложим отрезок A_x2A»₁ равный отрезку A»A_x1.

Использование метода замены при решении задач

Владея методом замены применительно к одной точке, можно построить дополнительные проекции любых фигур, поскольку они представляют собой множество точек. На рисунке ниже показан перевод отрезка AB в частное положение. Новая плоскость П₄ проведена параллельно AB, поэтому отрезок проецируется на неё в натуральную величину.

На следующем рисунке показана плоскость общего положения α, заданная следами. Переведем её в новую систему плоскостей П₁, П₄ так, чтобы α занимала проецирующее положение. Для этого перпендикулярно горизонтальному следу h_0α введем дополнительную фронтальную плоскость П₄.

Новый фронтальный след f_0α1 строится по двум точкам. Одна из них, X_α1, лежит на пересечении h_0α с осью x₁. Дополнительно возьмем точку N, принадлежащую α, и укажем её фронтальную проекцию N»₁ на плоскости П₄.

Определение расстояния между параллельными плоскостями

Параллельные плоскости α и β расположены так, как показано на рисунке. Чтобы найти расстояние между ними, необходимо из произвольной точки A, взятой на пл. α, опустить перпендикуляр AB на пл. β и определить его настоящую длину.

Для уменьшения количества геометрических построений α и β предварительно переводятся в проецирующее положение с помощью метода замены плоскостей проекций. Вспомогательная точка M используется для определения направления следов f_0β1 и f_0α1, параллельных друг другу.

Источник