Способы замены плоскостей проекций начертательная геометрия

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф Ф.,

5.3. Преобразование комплексного чертежа способом замены плоскостей проекций

Рассмотрим решение задач, используя способ замены плоскостей проекций. При этом способе объект сохраняет своё положение в пространстве,а положение плоскостей проекций последовательно меняется. Любые две взаимно перпендикулярные плоскости могут быть приняты за новую систему плоскостей проекций, но при этом понятие горизонтальной и фронтальной плоскостей проекций сохраняется.

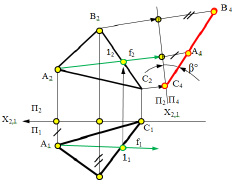
Задача №1. Преобразовать комплексный чертеж так, чтобы прямая общего положения АВ оказалась параллельной одной из плоскостей проекций т.е. прямой уровня (горизонталь или фронталь) новой системы (рис. 5.1).

Для решения задачи необходимо заменить плоскость проекций П1, или П2 новой плоскостью проекций П4, параллельной прямой АВ и перпендикулярной к незаменяемой плоскости проекций.

Такая задача решается на комплексном чертеже при необходимости определения натуральной длины отрезка прямой и угла наклона этого отрезка к плоскостям проекций. Для того чтобы прямая АВ в новой системе плоскостей проекций стала, например, фронталью, нужно заменить фронтальную плоскость проекций П2новой плоскостью П4 ⊥ П1 и параллельной прямой АВ.

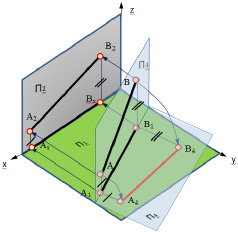
Рис. 5.1. Изображение в пространстве преобразования прямой линии
общего положения в прямую линию уровня

Рассмотрим подробно этапы построения на комплексном чертеже (рис. 5.2), необходимые для решения первой основной задачи на преобразование комплексного чертежа:

1) провести новую ось проекций х14 параллельно А1В1 на произвольном расстоянии от нее; такое положение оси х14 обусловливается тем, что П4 параллельна АВ. В частном случае, если плоскость П4 проведена непосредственно через прямую АВ, ось х14 = А1В1;

2) выбрать на прямой две точки А(А1А2) и В(В1В2);

3) построить проекции точек А и В на плоскости П4.

Прямая А4В4 является проекцией прямой АВ на плоскость П4. Прямая AB в новой системе плоскостей проекций П1/П4 является фронталью.

Отрезок [АВ] прямой проецируется на плоскость П4 в истинную величину, т.е. |А4В4| = |АB|, α°– величина угла наклона прямой АВ к плоскости П1.

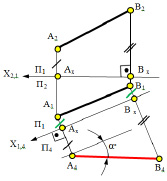
Рис. 5.2. Изображение преобразования прямой линии общего положения
в прямую линию уровня

3адача 2. Преобразовать комплексный чертеж так, чтобы линия общего положения АВ стала проецирующей (рис. 5.3).

Для решения задачи необходимо выполнить две замены плоскостей проекций – заменить фронтальную плоскость проекций П2 исходной системы П2/П1 вспомогательной проецирующей плоскостью П4 || А1В1.При этом плоскость П4 будет перпендикулярной П1 так как АВ || П4 и образует с ней новую систему плоскостей проекций П1/П4.

Построения на комплексном чертеже:

1) провести новую ось проекций х14 || А1В1;

2) построить проекции точек А и В на плоскости П4, взяв координаты точек из плоскости П2;

3) заменить плоскость П1 на новую П5, которая будет ⊥ А4В4. Для этого нужно провести новую ось проекций х4,5.

Так как расстояния точек А и В до плоскости П4 одинаковы, то проекции их на плоскости П5 совпадут, А5 ≡ В5, прямая АВ (А5В5) в новой системе плоскостей проекций займёт проецирующее положение и станет горизонтально проецирующей.

Прямую линию общего положения преобразовать в проецирующую линию, заменой, только одной плоскости проекций, нельзя, потому, что плоскость П5 перпендикулярная прямой, не будет перпендикулярна ни одной из «старых» плоскостей проекций, и, следовательно, не сможет образовать, ни с одной из них, прямоугольной системы плоскостей проекций. Для того, чтобы, прямую общего положения преобразовать в проецирующую, необходимо выполнить две последовательные замены плоскостей проекций: прямую общего положения следует преобразовать в линию уровня, а затем линию уровня преобразовать в проецирующую (рис. 5.3).

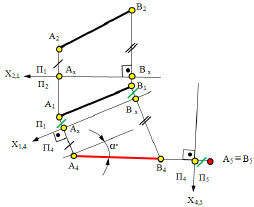
Рис. 5.3. Изображение преобразования прямой линии АВ общего положения
в прямую горизонтально-проецирующую линию.

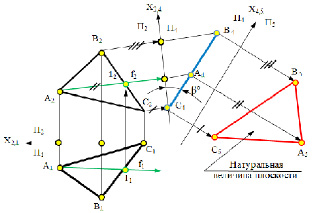
Задача №3. Преобразовать комплексный чертеж так, чтобы плоскость общего положения стала проецирующей (рис. 5.4, 5.5).

Для решения задачи необходимо заменить плоскость П1 или П2исходной системы П2/П1 новой плоскостью П4, перпендикулярной плоскости (АВС).

Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Следовательно, если какую-либо прямую, принадлежащую плоскости , преобразовать в проецирующую, то данная плоскость в новой системе плоскостей проекций станет проецирующей. Проще всего для этой цели воспользоваться линией уровня.

На рис. 5.4 плоскость (АВС) общего положения преобразована во фронтально-проецирующую путем преобразования её горизонтали h(h1,h2), во фронтально-проецирующее положение. В новой системе плоскостей проекций П1/П4 плоскость является фронтально проецирующей ( ⊥ П4), и поэтому её проекция на П4 вырождается в прямую линию 4 (С4, А4, В4).

В этом случае α° – величина угла наклона плоскости к плоскости П1.

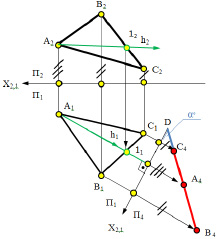
Рис. 5.4. Преобразование плоскости общего положения
в проецирующую плоскость для определения угла наклона α°к П1

Для определения угла наклона (β°), заданной плоскости к фронтальной плоскости проекций (П4), необходимо выполнить преобразования построения, аналогичные преобразованиям, рассмотренным выше (рис.5.5), используя фронталь.

Рис. 5.5. Преобразование плоскости общего положения
в проецирующую плоскость для определения угла наклона β° к П2

В этом случае плоскость преобразуется в горизонтально проецирующую плоскость с помощью её фронтали, которая преобразуется в горизонтально – проецирующую линию.

Задача № 4. Преобразовать комплексный чертеж так, чтобы плоскость общего положения стала плоскостью уровня (параллельной одной из плоскостей проекций) новой системы (рис.5.6).

Плоскость общего положения преобразовать в плоскость уровня заменой только одной плоскости проекций нельзя, так как плоскость П4, параллельная ей, не будет перпендикулярна ни одной из старых плоскостей проекций и, следовательно, не образует ни с одной из них прямоугольной системы плоскостей проекций.

Для того чтобы плоскость общего положения преобразовать в плоскость уровня, необходимо выполнить две последовательные замены плоскостей проекций. В начале решения плоскость необходимо преобразовать в проецирующую, т. е. решить задачу 3 на преобразование комплексного чертежа, а затем проецирующую плоскость преобразовать в плоскость уровня.

На рис. 5.6 показан алгоритм преобразования плоскости Δ(АВС) в плоскость уровня.

Рис. 5.6. Решение задачи на преобразование плоскости общего положения
в плоскость уровня.

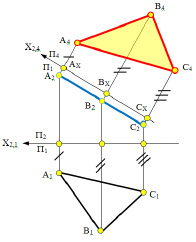
Рассмотрим ещё один возможный вариант (рис. 5.7). Допустим, что необходимо определить натуральную величину фронтально проецирующей плоскости Г(ΔАВС). Для этого заменим плоскость П1 новой плоскостью проекций П4, параллельной плоскости Г(ΔАВС) и, перпендикулярной незаменяемой плоскости П1. В новой системе плоскостей проекций П2/П4 плоскость Г(АВС) станет плоскостью уровня новой плоскости проекций.

Построения на комплексном чертеже:

1) провести новую ось проекций х2,4 параллельно А2С2 на произвольном от нее расстоянии;

2) построить проекции точек А, В и С на плоскость П4;

3) треугольник А4В4С4 является проекцией плоскости треугольника АВС на плоскость П4.

Примечание. Так как плоскость треугольника АВС параллельна П4, значит отображение этого треугольника на П4 величина натуральная. Значит, третья задача на преобразование плоскости уже решена и для решения четвёртой задачи необходимо выполнить одну замену плоскостей проекций. Необходимо горизонтальную плоскость проекций заменить на плоскость П4 и создать новую систему П2 /П4.

Рис. 5.7. Решение четвертой задачи на преобразование фронтально проецирующей плоскости в плоскость уровня

Источник

СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ

Решение пространственных задач на комплексном чертеже значительно упрощается, если интересующие нас элементы фигуры занимают частное положение.

Переход от общего положения геометрической фигуры к частному выполняется следующим способом: введением дополнительных плоскостей проекций, расположенных либо параллельно, либо перпендикулярно рассматриваемому геометрическому элементу.

Сущность способа заключается в том, что пространственное положение объекта не изменяют, а вводят новую, дополнительную плоскость проекций, расположенную таким образом, чтобы интересующие нас элементы фигуры или весь объект целиком проецировался на неё в удобном для решения задачи положении. При этом новая плоскость проекций должна быть перпендикулярна к одной из имеющихся плоскостей проекций. В результате образуется новая система взаимно перпендикулярных плоскостей проекций, заменяющая прежнюю.

На рис. 54 в систему плоскостей проекций введем новую плоскость проекций . Новой осью проекций будет . Заметим, что координаты Z точек А и В в плоскостях и будет одна и та же. И кроме того, если новую ось выберем параллельно проекции прямой , то на плоскости проекций проекция проектируется в натуральную величину прямой АВ.

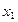
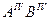
ПЕРЕВОД ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ В ПОЛОЖЕНИЕ ПРЯМОЙ УРОВНЯ

(т.е. параллельно новой плоскости проекций )

Для преобразования прямой АВ в прямую уровня (рис. 55) вводят новую плоскость проекций так, чтобы ось проекций была параллельна проекции (рис. 54), затем откладывают на новой плоскости проекций от оси ( ) координаты Z точек и , равные координатам Z точек и .

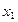
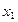
Новая проекция прямой дает натуральную величину отрезка АВ и угол наклона прямой к плоскости проекций .

ПЕРЕВОД ПРЯМОЙ УРОВНЯ В ПРОЕЦИРУЮЩЕЕ ПОЛОЖЕНИЕ

(т.е. перпендикулярно плоскости проекций)

Чтобы на новой плоскости проекций изображение прямой уровня преобразовалось в точку (рис. 56), надо эту плоскость расположить перпендикулярно данной прямой, т.е. провести на комплексном чертеже ось проекций перпендикулярно направлению проекции прямой на общую плоскость проекций. Горизонталь будет иметь своей проекцией точку на плоскости .

Для построения вырожденной в точку проекции прямой общего положения необходимо последовательно решить две предыдущие задачи: на рис. 57 представлено такое решение.

ПЕРЕВОД ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ В ПРОЕЦИРУЮЩЕЕ

Известно, что если одна плоскость перпендикулярна другой, то она должна содержать прямую, перпендикулярную этой плоскости. В качестве такой прямой можно взять прямую уровня, например, горизонталь, как это показано на рис. 58.

Переведем горизонталь h в проецирующее положение, вводя новую плоскость проекций . Поскольку проекция плоскости АВС на плоскости вырождена ыв прямую, она будет служить геометрическим местом всех точек, принадлежащих этой плоскости. Проецируем точки плоскости на , беря их координаты Z с плоскости .

ПЕРЕВОД ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТИ В ПОЛОЖЕНИЕ ПЛОСКОСТИ УРОВНЯ

Решение этой задачи позволяет определить натуральную величину плоской фигуры (рис. 59.).

Пусть задана фронтально-проецирующая плоскость . Вводим новую плоскость проекций , параллельную . Новая ось проекций по этой причине будет расположена параллельно , т.е. в системе плоскостей проекций плоскость займет положение плоскости уровня, а треугольник АВС будет проецироваться на плоскость в натуральную величину.

Если в исходном положении плоскость занимает общее положение, а нужно получить её изображение как плоскости уровня, то прибегают к двойной замене плоскостей проекций, решая последовательно две предыдущие задачи. При первой замене плоскость становится проецирующей (вырождается в линию), а при второй – плоскостью уровня (рис. 60 – не приведён). Расстояние для построения проекций точек на плоскости нужно брать с плоскости , отмеряя их от оси проекций .

Источник