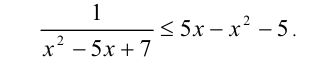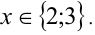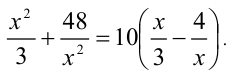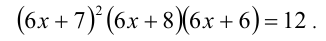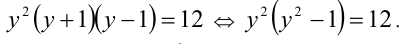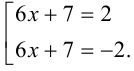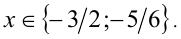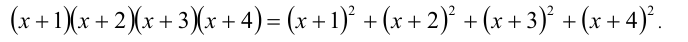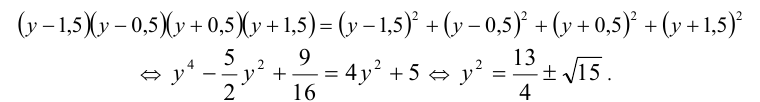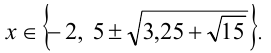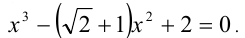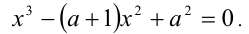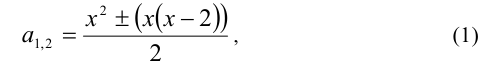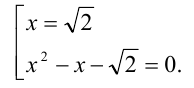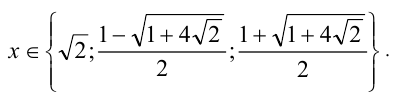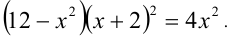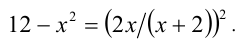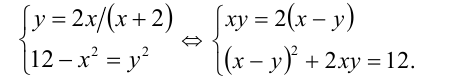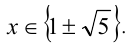«Решение показательных уравнений с помощью замены переменных». 11-й класс
Разделы: Математика
Класс: 11
Цель урока: изучить способ решения показательных уравнений с помощью замены переменных.
– повторить известные способы решения показательных уравнений;
– показать алгоритм решения с помощью замены переменных;
– создавать условия для формирования навыков организации своей деятельности – самостоятельного поиска решения, самоконтроля;
– приучать к аккуратности выполнения записей в тетради и на доске;
– воспитывать умение работать в парах, взаимопомощь;
– воспитывать умение анализировать результаты своей деятельности;
– формировать умение сравнивать, выявлять закономерности, обобщать;
– формировать грамотную математическую речь;
– формировать умение применять знания в конкретной ситуации.
Преподавание ведется по учебнику А.Н.Колмогорова.
Сегодня мы продолжим знакомство с методами решения показательных уравнений.
Запишите тему урока: “Решение показательных уравнений”, но оставьте строчку, тему мы чуть позже уточним.
2. Актуализация знаний.
Устная работа с классом.
1)  =32; | 5)  = – 25; |
2)  =81; | 6)  ; |
3)  = ; | 7)  = ; |
4)  =27; | 8)  . |
3. Постановка проблемы.
Уравнения 1 – 7 решали, приводя их к виду 
или 
. Последнее уравнение решить таким способом не удается.
Обратите внимание: 
. Предложите способ решения. Нужно ввести новую переменную у = 
и решить полученное квадратное уравнение.
Какова будет наша цель сегодня? Научиться решать показательные уравнения с помощью замены переменных.
Уточним тему урока: “Решение показательных уравнений с помощью замены переменных”.
4. Изучение нового материала.
Пусть у = 
, причем у > 0.
Уравнение примет вид 
.
Решим это уравнение: 
= –1; 
= 5.
не удовлетворяет условию у > 0.
= 5; х = 1.
Решим уравнение 
.
Перепишем его в виде 
.
Далее решает ученик у доски с комментированием.
Пусть 
, причем у > 0.
3у – 8 = 
; 3
– 8у = 3; 3– 8у – 3 = 0;
Решим это уравнение: = –
; = 3.
не удовлетворяет условию у > 0.
= 3; х = 1.
Решим уравнение 
.
Почему не удается решить? Нельзя привести степени к одному основанию.
Перепишем уравнение в виде 
Разделим обе части уравнения на 
: 
.
Далее решает у доски ученик с комментированием.
Пусть у =
, причем у > 0.
Уравнение примет вид 
.
.
Решим это уравнение: = 1; =
.
= 1; х = 0. = 
; х = 1.
Можно было делить на 
? Что изменилось бы в решении? Ввели бы обозначение у =
.
5. Первичное закрепление изученного материала.
Ученики работают в парах, более сильные ребята помогают соседям.
Два ученика работают за крыльями доски.
 . Перепишем в виде Пусть у +
Решим это уравнение:
Ответ: 1; 2. |  Разделим обе части уравнения на Пусть у = Уравнение примет вид Решим это уравнение:
Ответ: |
.
= 12;
: 
.
, причем у > 0.
.
.
; 
; 
= 2; х = 
.
.6. Самостоятельная работа.
Чтобы проверить, как усвоен новый материал, выполните самостоятельную работу.
1) 
;
2) 
;
3) 
.
По окончании работы ученики самостоятельно проверяют решение по образцу (раздаточный материал), фиксируя места, где допущены ошибки.
7. Итог урока.
- Обсуждение результатов самостоятельной работы.
- Кто выполнил правильно все задания?
- Кто допустил ошибки в первом (втором, третьем) задании? Какие?
- Повторим, какие приемы использовали при решении показательных уравнений.
- Оцените свою работу на уроке.
- Вам предстоит еще раз применить полученные знания при выполнении домашнего задания: № 464(в,г), 470(в,г), 166(г) (стр. 299).
Источник
Метод замены переменных при решении уравнений и неравенств
Метод замены переменных
Этот распространённый метод используется для разных целей: упрощение задачи и повышение её наглядности, придание уравнению (неравенству, системе и проч.) более симметричного вида, сведение одного уравнения к системе нескольких уравнений, рационализация иррациональностей (см. пункт 3.3) и т.д. Иными словами, введение новых переменных производится в тех случаях, когда есть возможность свести задачу к другой, для которой существует более эффективный способ решения.
Существуют виды уравнений, для которых разработаны специальные подстановки, позволяющие наиболее оптимально решать эти уравнения (например, симметрические и возвратные уравнения, однородные уравнения и многие другие). Рассмотрим дополнительно группу примеров, иллюстрирующих различные цели использования этого подхода.
Начнём с примера, в котором при помощи замены неизвестной рациональное неравенство сводится также к рациональному, но более простому алгебраическому неравенству.
Пример №350.
Решение:
Положим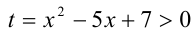 
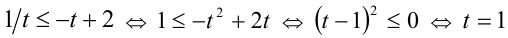
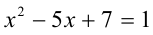
. Тогда необходимо решить неравенство 
. Выполнив обратную подстановку, получим квадратное уравнение 
, решив которое, приходим к ответу. Ответ:
В следующем примере дробно-рациональное уравнение заменой сводится к целому алгебраическому уравнению.
Пример №351.
Решить уравнение 
Решение:
Обозначим разность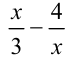 
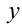
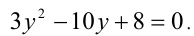
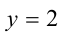
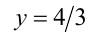
через 
, тогда уравнение перепишется в виде 
Это уравнение имеет два корня 
и 
, что приводит к совокупности уравнений
Первое уравнение даёт корни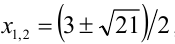 
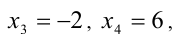
, а второе — 
которые и будут решениями исходного уравнения.
В некоторых случаях алгебраическую задачу (даже если в её условиях не содержится радикалов) с помощью специальных тригонометрических подстановок бывает целесообразно свести к тригонометрической задаче, и далее уже решать её методами тригонометрии.
Пример №352.
Известно, что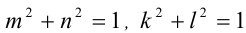 
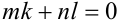
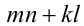
и 
. Чему равно значение 
?
Решение:
Воспользуемся тем, что если два действительных числа X, у удовлетворяют равенству
где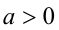 
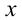
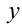
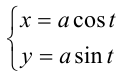
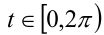
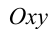
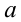
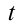
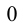
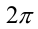
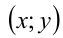
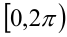
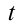
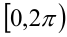
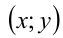
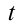
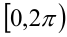
— заданное число, то 
и можно представить в тригонометрическом виде 
, где 
. В самом деле, уравнение (1) задаёт на плоскости 
окружность радиуса 
с центром в начале координат. При изменении 
от 
до 
точка с координатами 
ровно один раз обходит окружность, и таким образом между точками окружности и полуинтервалом 
оказывается установлено взаимно однозначное соответствие. Это означает, что каждому значению из соответствует единственная пара чисел , удовлетворяющих равенству (1), и наоборот, каждой паре чисел, удовлетворяющих (1), соответствует единственное значение из .
Итак, поскольку числа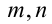 
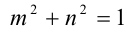
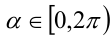
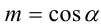
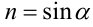
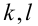
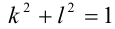
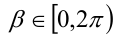
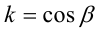
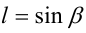
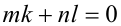
удовлетворяют равенству 
, то найдётся такое число 
, что 
, 
. Аналогично, поскольку числа 
удовлетворяют равенству 
, то найдётся такое число
, что 
, 
. При этом условие 
примет вид
Выполнив тригонометрическую подстановку в искомом выражении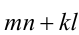 
, получим:
Введение новых переменных может быть вызвано необходимостью понизить степень уравнения, упростив при этом решение задачи.
Пример №353.
Решить уравнение 
Решение:
Сведём данное уравнение 4-й степени к квадратному уравнению. Для этого вначале умножим обе части уравнения на 12 и приведём его к виду
Затем сделаем подстановку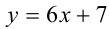 
, что приведёт к уравнению
Сделав ещё одну подстановку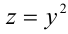 
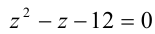
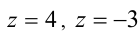
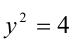
, сведём окончательно данное биквадратное уравнение к квадратному уравнению 
, решив которое, находим корни 
. Тогда 
и 
Ответ: 
В следующем примере используется симметризирующая подстановка. Название говорит само за себя: уравнению придаётся более «симметричный» вид. Новая переменная является средним арифметическим входящих в уравнение выражений. При её применении уравнение 4-й степени общего вида приводится к более простому частному случаю, а именно, симметризация уравнения позволяет «убрать» из уравнения нечётные степени неизвестной, оставив только чётные и превратив его, таким образом, в биквадратное уравнение.
Пример №354.
Решение:
Выполним симметризирующую подстановку
Тогда уравнение примет вид
Ответ: 
6.Близко к методу введения новых переменных стоит так называемый метод введения параметра. Не всегда введение параметра усложняет задачу. На примере, рассмотренном ниже, видно, как включение параметра в уравнение вместо числового коэффициента позволяет лучше «разглядеть» способ дальнейшего его решения — рассмотрение уравнения как квадратного относительно введённой величины.
Пример №355.
Решение:
Введём в уравнение параметр, положив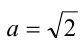 
:
Рассмотрим теперь это уравнение как квадратное относительно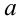 
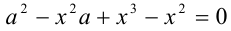
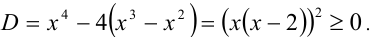
. Приведём его к стандартному виду 
и вычислим дискриминант 
Найдём корни:
т.е.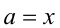 
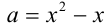
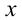
или 
. Параметр к этому моменту сыграл свою положительную роль, позволив свести решение кубического относительно уравнения к совокупности двух уравнений более низкой степени: квадратного и линейного.
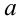
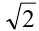
Заменяя числом 
, получим совокупность
Отсюда находим решения: 
Замечание. В формуле корней квадратного уравнения более корректным было, вообще говоря, написать
Однако когда ищутся оба корня, то использование формул (1) и (2) приводит к одному результату. Именно поэтому часто в подобных ситуациях модуль опускают.
7.Отметим, что, вообще говоря, не всегда в задаче нужно полностью переходить к новым переменным. Иногда имеет смысл, вводя новую переменную, сохранить в задаче и первоначальную переменную, т.е. сделать частичную замену переменных. Так, сведением к системе уравнений, решаются некоторые уравнения. Рассмотрим в качестве пояснения пример.
Пример №356.
Решение:
Так как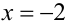 
не является корнем, то уравнение можно привести к равносильному виду
Положим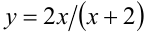 
, тогда уравнение сведётся к равносильной ему системе
Решая эту систему относительно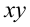 
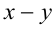
и 
, приходим к ответу: 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник
