Закон распределения дискретной случайной величины. Примеры решения задач
Как известно, случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая. Случайные величины обозначают заглавными буквами латинского алфавита (X, Y, Z), а их значения – соответствующими строчными буквами (x, y, z). Случайные величины делятся на прерывные (дискретные) и непрерывные.
Дискретной случайной величиной называется случайная величина, принимающая лишь конечное или бесконечное (счетное) множество значений с определенными ненулевыми вероятностями.
Законом распределения дискретной случайной величины называется функция, связывающая значения случайной величины с соответствующими им вероятностями. Закон распределения может быть задан одним из следующих способов.
1. Закон распределения может быть задан таблицей:
| Значения xi | x1 | x2 | x3 | . | xn |
| Вероятности pi | p1 | p2 | p3 | . | pn |
События X = xi (i = 1, 2, 3,…,n) являются несовместными и единственно возможными, т.е. они образуют полную систему событий. Поэтому сумма их вероятностей равна единице: р1+р2+р3+…+рn = ∑pi =1
2. Закон распределения может быть задан аналитически (формулой) P(X = xi) = ϕ(xi). Например:
а) с помощью биномиального распределения: Pn(X=k) = Сn k p k q n-k , 0 0, k = 0, 1, 2, … .
в) с помощью функции распределения F(x), определяющей для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т.е. F(x) = P(X 2 или D(X) = M(X 2 )−[M(X)] 2 . Разность X–M(X) называют отклонением случайной величины от ее математического ожидания.
Для биномиального распределения D(X)=npq, для распределения Пуассона D(X)=λ
Примеры решения задач по теме «Закон распределения дискретной случайной величины»
Задача 1.
Выпущено 1000 лотерейных билетов: на 5 из них выпадает выигрыш в сумме 500 рублей, на 10 – выигрыш в 100 рублей, на 20 – выигрыш в 50 рублей, на 50 – выигрыш в 10 рублей. Определить закон распределения вероятностей случайной величины X – выигрыша на один билет.
Решение. По условию задачи возможны следующие значения случайной величины X: 0, 10, 50, 100 и 500.
Число билетов без выигрыша равно 1000 – (5+10+20+50) = 915, тогда P(X=0) = 915/1000 = 0,915.
Аналогично находим все другие вероятности: P(X=0) = 50/1000=0,05, P(X=50) = 20/1000=0,02, P(X=100) = 10/1000=0,01, P(X=500) = 5/1000=0,005. Полученный закон представим в виде таблицы:
| Значения xi | 0 | 10 | 50 | 100 | 500 |
| Вероятности pi | 0,915 | 0,05 | 0,02 | 0,01 | 0,005 |
Задача 2.
Найти математическое ожидание числа очков, выпадающих при бросании игральной кости.
Решение. Случайная величина X числа очков принимает значения 1, 2, 3, 4, 5, 6. Вероятность того, что выпадет одно из данных значений равна 1/6. Закон распределения представим в виде таблицы:
| Значения xi | 1 | 2 | 3 | 4 | 5 | 6 |
| Вероятности pi | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Найдем математическое ожидание величины Х: М(Х) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = (1+2+3+4+5+6)/6 = 21/6 = 3,5
Задача 3.
Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте, построить многоугольник распределения. Найти функцию распределения F(x) и построить ее график. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины.
Решение. 1. Дискретная случайная величина X= <число отказавших элементов в одном опыте>имеет следующие возможные значения: х1=0 (ни один из элементов устройства не отказал), х2=1 (отказал один элемент), х3=2 (отказало два элемента) и х4=3 (отказали три элемента).
Отказы элементов независимы друг от друга, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n=3, р=0,1, q=1-р=0,9, определим вероятности значений:
P3(0) = С3 0 p 0 q 3-0 = q 3 = 0,9 3 = 0,729;
P3(1) = С3 1 p 1 q 3-1 = 3*0,1*0,9 2 = 0,243;
P3(2) = С3 2 p 2 q 3-2 = 3*0,1 2 *0,9 = 0,027;
P3(3) = С3 3 p 3 q 3-3 = р 3 =0,1 3 = 0,001;
Проверка: ∑pi = 0,729+0,243+0,027+0,001=1.
Таким образом, искомый биномиальный закон распределения Х имеет вид:
| Значения xi | 0 | 1 | 2 | 3 |
| Вероятности pi | 0,729 | 0,243 | 0,027 | 0,001 |
2. Для построения многоугольника распределения строим прямоугольную систему координат.
 |
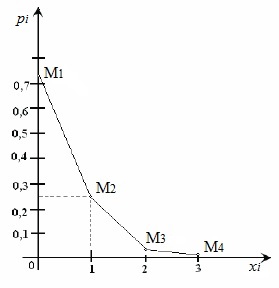По оси абсцисс откладываем возможные значения хi, а по оси ординат – соответствующие им вероятности рi. Построим точки М1(0; 0,729), М2(1; 0,243), М3(2; 0,027), М4(3; 0,001). Соединив эти точки отрезками прямых, получаем искомый многоугольник распределения.
3. Найдем функцию распределения F(x) = Р(Х 3 будет F(x) = 1, т.к. событие достоверно.
 |
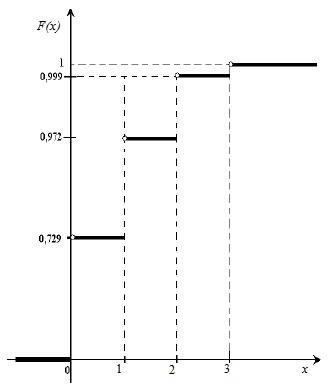— график функции F(x)
4. Для биномиального распределения Х:
— математическое ожидание М(X) = np = 3*0,1 = 0,3;
— дисперсия D(X) = npq = 3*0,1*0,9 = 0,27;
— среднее квадратическое отклонение σ(X) = √D(X ) = √0,27 ≈ 0,52.
Другие статьи по данной теме:
Список использованных источников
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике / М. — «Высшая школа», 2004;
- Лисьев В.П. Теория вероятностей и математическая статистика: Учебное пособие/ Московский государственный университет экономики, статистики и информатики. – М., 2006;
- Семёнычев В. К. Теория вероятности и математическая статистика: Лекции /Самара, 2007;
- Теория вероятностей: контрольные работы и метод. указания для студентов / сост. Л.В. Рудная и др. / УрГЭУ — Екатеринбург, 2008.
2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна
Источник
Способы задания случайных величин
Основные распределения
Случайных величин
Методические указания для самостоятельной работы студентов
всех форм обучения
Составитель В.А. Бобкова
Составитель В.А. Бобкова
Основные распределения случайных величин: Методические указания для самостоятельной работы студентов всех форм обучения/ Сост. В. А. Бобкова; ГОУВПО Иван. гос. хим.-технол. ун-т. – Иваново, 2005. 32 с.
Методические указания посвящены одному из важных разделов курса «Теория вероятностей и математическая статистика», а именно: основным распределениям случайных величин. Дано понятие случайной величины, описаны способы задания дискретных и непрерывных случайных величин, приведены определения математического ожидания, дисперсии, среднеквадратического отклонения. Далее рассмотрены основные распределения дискретных случайных величин: распределение Бернулли, биномиальное распределение, распределение Пуассона, геометрическое и гипергеометрическое распределения, а также основные распределения непрерывных случайных величин: равномерное, показательное, нормальное распределения. Выведены формулы для числовых характеристик рассмотренных распределений, приведены графические иллюстрации и примеры решения задач. Даны задачи для самостоятельного решения.
Методические указания предназначены для самостоятельной работы студентов всех специальностей вуза.
Библиогр.: 4 назв.
Рецензент доктор технических наук, профессор А. Н. Лабутин
(Ивановский государственный химико-технологический университет)
Основные сведения о случайных величинах
Понятие случайной величины
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, заранее не известное и зависящее от случайных причин, которые не могут быть учтены.
Случайные величины обозначаются прописными латинскими буквами X,Y, Z, …, а их возможные значения – соответствующими строчными буквами x, y, z, … .
Примеры случайных величин:
1) число вызовов, поступивших от абонентов на телефонную станцию в течение определённого времени;
2) вес наугад взятого зерна пшеницы;
3) число отличных оценок у студентов одной группы на экзамене;
4) расстояние от точки метания диска до точки падения;
5) число опечаток в книге.
Разнообразие случайных величин велико. Число принимаемых ими значений может быть конечным, счётным или несчетным; эти значения могут быть расположены дискретно или заполнять интервалы (конечные или бесконечные).
Дискретные случайные величины – это случайные величины, которые могут принимать только конечное или счетное множество значений. Например, число появлений герба при пяти подбрасываниях монеты (возможные значения 0, 1, 2, 3, 4, 5); число выстрелов до первого попадания в цель (возможные значения 1, 2, … , n, где n – число имеющихся в наличии патронов); число отказавших элементов в приборе, состоящем из трех элементов (возможные значения 0, 1, 2, 3) – это дискретные случайные величины.
Непрерывные случайные величины – это случайные величины, возможные значения которых образуют некоторый конечный или бесконечный интервал. Например, время безотказной работы прибора, дальность полёта снаряда, время ожидания автобуса – это непрерывные случайные величины.
Способы задания случайных величин
Для того, чтобы задать случайную величину, надо знать те значения, которые она может принимать, и вероятности, с которыми случайная величина принимает свои значения. Любое правило (таблица, функция, график), позволяющее находить вероятности отдельных значений случайной величины или множества этих значений, называется законом распределения случайной величины (или просто распределением). Про случайную величину говорят, что «она подчиняется данному закону распределения».
Пусть X –дискретная случайная величина, которая принимает значения 
(множество этих значений конечно или счетно) с некоторыми вероятностями 
. Закон распределения дискретной случайной величины удобно задавать с помощью формулы 
i = 1, 2, 3, … , n, … , определяющей вероятность того, что в результате опыта случайная величина X примет значение 
. Для дискретной случайной величины закон распределения может быть задан в виде таблицы распределения:
| X |  |  | … |  | … |
| P |  |  | … | pn | … |
Здесь первая строка содержит все возможные значения (обычно в порядке возрастания) случайной величины, а вторая – их вероятности. Такую таблицу называют рядом распределения.
Так как события 
несовместны и образуют полную группу событий, то сумма их вероятностей равна единице.
Закон распределения дискретной случайной величины можно задать графически, если на оси абсцисс отложить возможные значения случайной величины, а на оси ординат – их вероятности. Ломаную, соединяющую последовательно полученные точки, называют многоугольником распределения.
Очевидно, что ряд распределения можно построить только для дискретных случайных величин. Для непрерывных случайных величин нельзя даже перечислить все возможные значения.
Универсальным способом задания закона распределения вероятностей, пригодным как для дискретных, так и для непрерывных случайных величин, является её функция распределения.
Пусть Х – случайная величина, х — действительное число. Функцией распределения вероятностей случайной величины Х называют вероятность того, что эта случайная величина примет значение, меньшее, чем х:
(1)
Геометрически это равенство можно истолковать так: F(x) есть вероятность того, что случайная величина X примет значение, которое изображается на числовой оси точкой, лежащей левее точки x, то есть что случайная точка X попадёт в интервал 
.
Свойства функции распределения:
1. Значения функции распределения принадлежат отрезку [0,1]:
(2)
2. F(x) – неубывающая функция, то есть 
если 
.
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале [a,b), равна приращению функции распределения на этом интервале:
(3)
Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна нулю.
3. Если возможные значения случайной величины принадлежат интервалу (a,b), то 
при 
и 
при 
.
Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси x, то справедливы следующие предельные соотношения:
(4)
Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности.
Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(x) – первую производную от функции распределения F(x):
. (5)
Из этого определения следует, что функция распределения является первообразной для плотности распределения.
Заметим, что для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.
Свойства плотности распределения:
1. Плотность распределения является неотрицательной функцией: 
для любого x. Это свойство следует из того, что функция распределения F(x) – неубывающая функция.
2. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b:
. (6)
Геометрически это можно истолковать так: вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна площади криволинейной трапеции, ограниченной осью Ox, кривой распределения f(x) и прямыми x = a и x = b (см. рис.1).
Рис. 1. График плотности распределения непрерывной случайной величины. Площадь S равна вероятности попадания случайной величины в интервал (a,b).
Следствие 1. Несобственный интеграл от плотности распределения в пределах от 
до 
равен единице:
(7)
Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ox и кривой распределения, равна единице (см. рис. 2).
Рис. 2. Площадь под графиком интегральной кривой равна единице.
Следствие 2. Зная плотность распределения f(x), можно найти функцию распределения F(x) по формуле:
. (8)
Действительно, если в формуле 
(6) перейти к пределу при 
; то 
. Следовательно, 
. Отсюда получается выражение (8) для F(x).
Итак, для того, чтобы некоторая функция была плотностью вероятностей, должны выполняться следующие условия:
а) функция должна быть неотрицательной;
б) должно выполняться равенство 
;
в) функция должна стремиться к 0 при 
.
Источник
