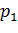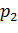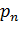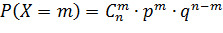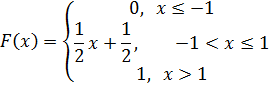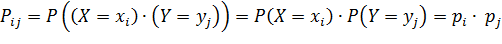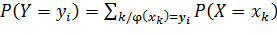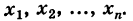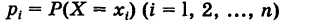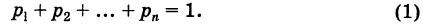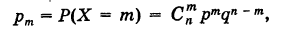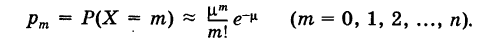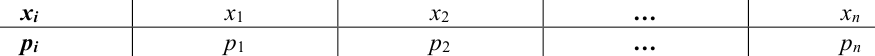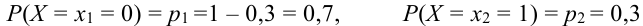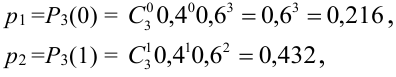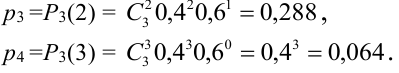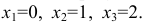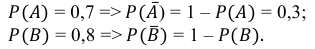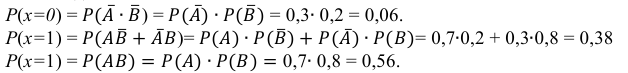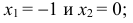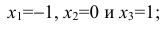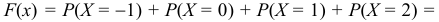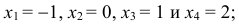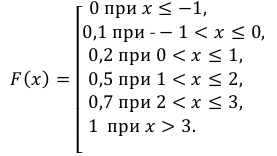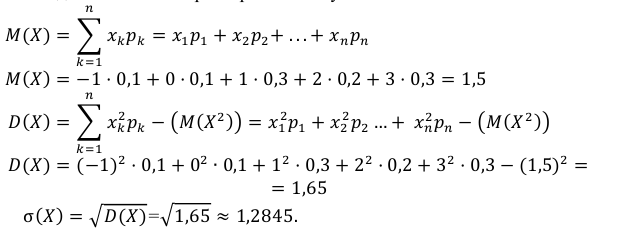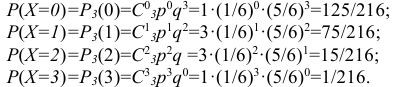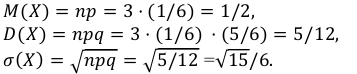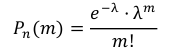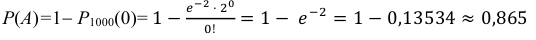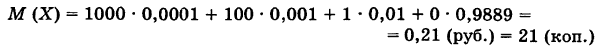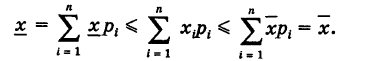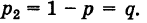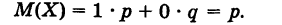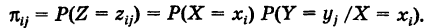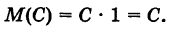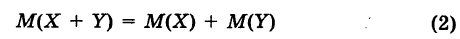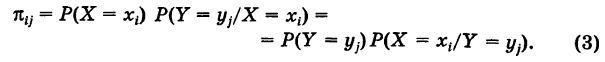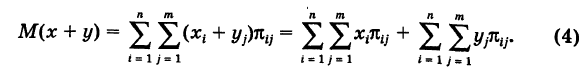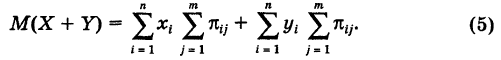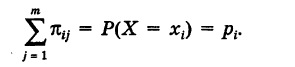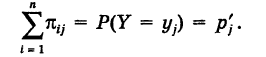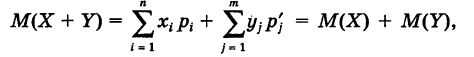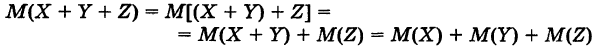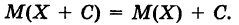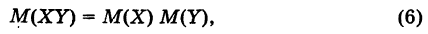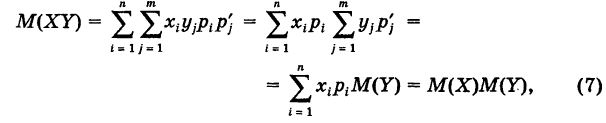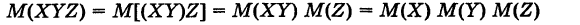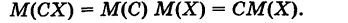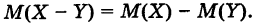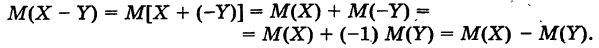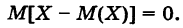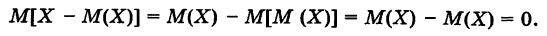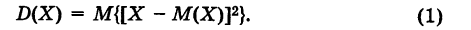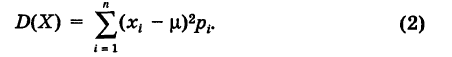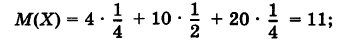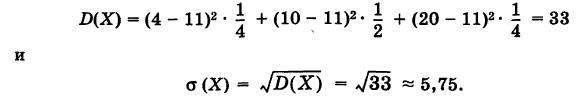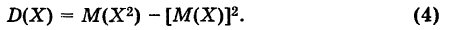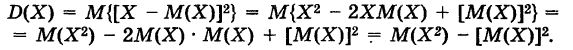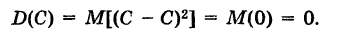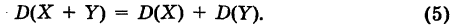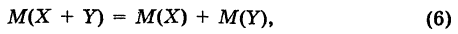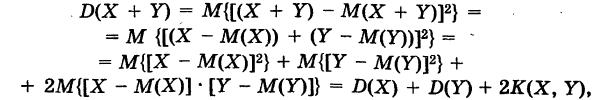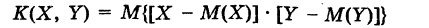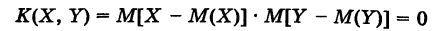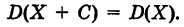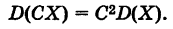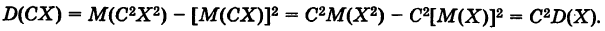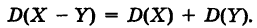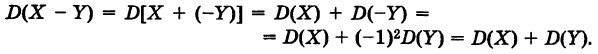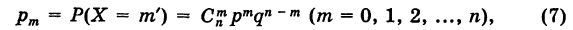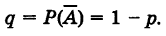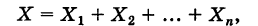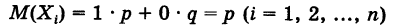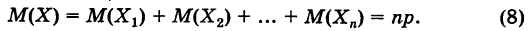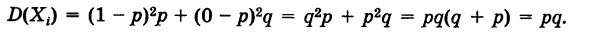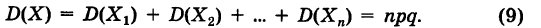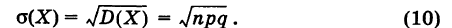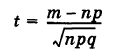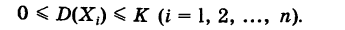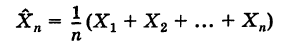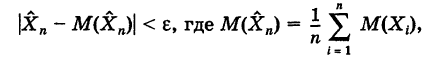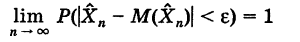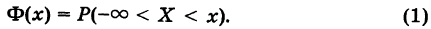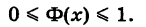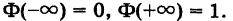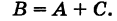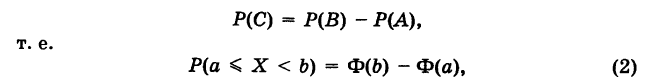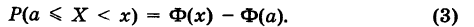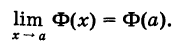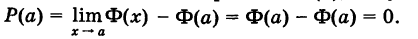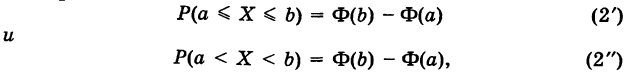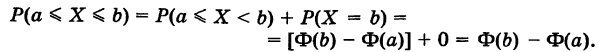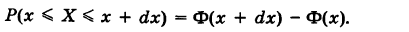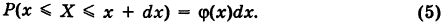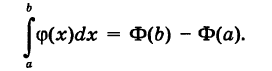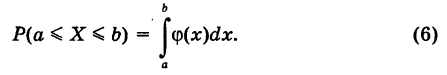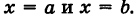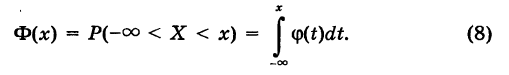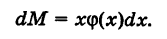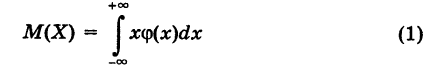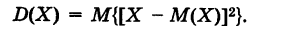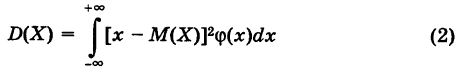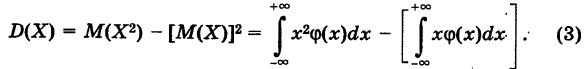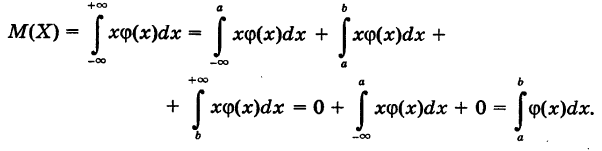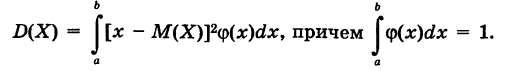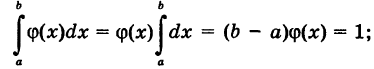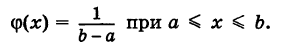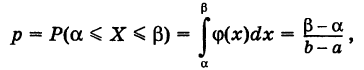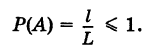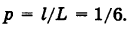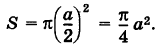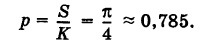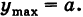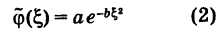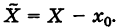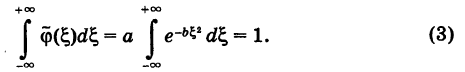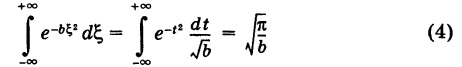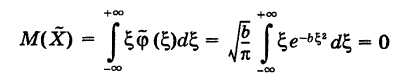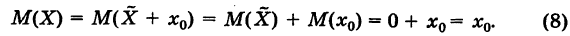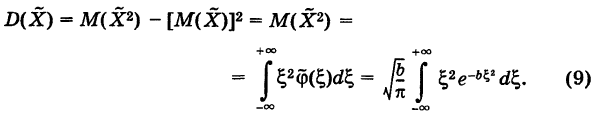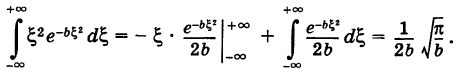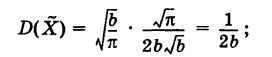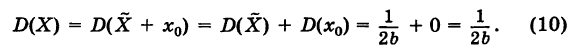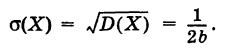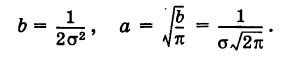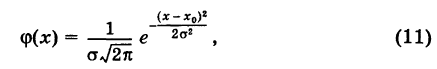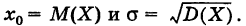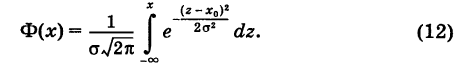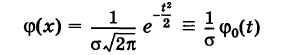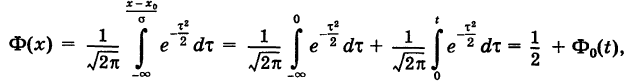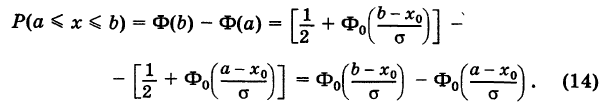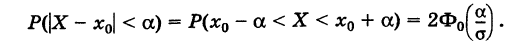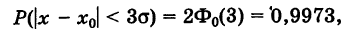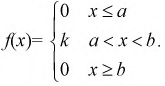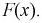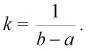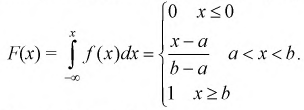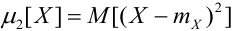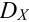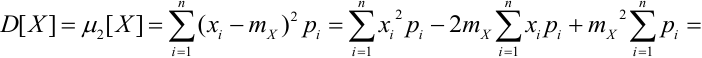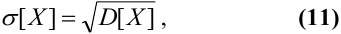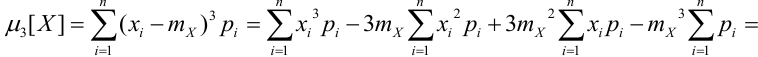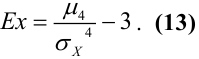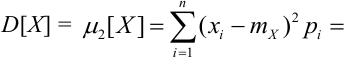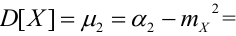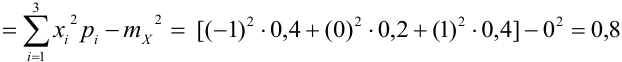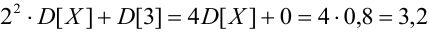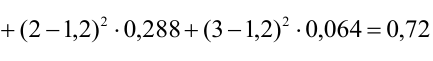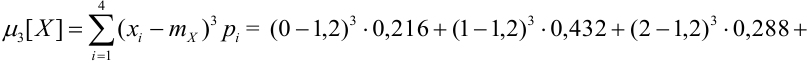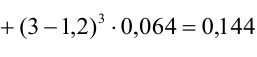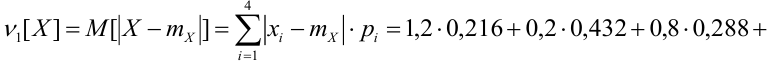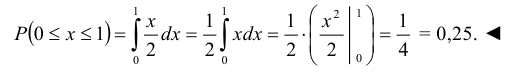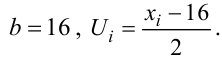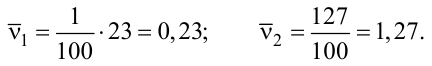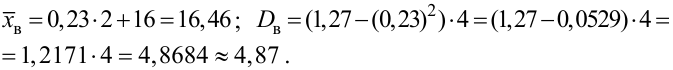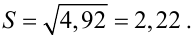- Случайные величины и способы их описания
- Случайные величины — определение и вычисление с примерами решения
- Определение случайной величины
- Примеры перехода от событий к случайным величинам
- Законы распределения случайных величин
- Формы закона распределения ДСВ
- Пример №1
- Пример №2
- Пример №3
- Пример №4
- Пример №5
- Пример №6
- Математическое ожидание
- Пример №7
- Основные свойства математического ожидания
- Дисперсия
- Пример №8
- Пример №9
- Непрерывные случайные величины. Функция распределения
- Числовые характеристики непрерывной случайной величины
- Равномерное распределение
- Пример №10
- Пример №11
- Нормальное распределение
- Пример №12
- Функция распределения — универсальный закон распределения (для ДСВ и НСВ)
- Пример №17
- Пример №18
- Пример №19
- Пример №61
Случайные величины и способы их описания



1. Дискретные и непрерывные случайные величины.
Среди задач, решаемых ТВ, очень много таких, в которых исход опыта выражается некоторым числом.
Случайной величиной (СВ) называется величина, которая при каждом осуществлении опыта принимает то или иное числовое значение, заранее неизвестно, какое именно.
Обозначение: X, Y, Z,… — случайные величины. Возможные значения случайных величин: x, y, z,… Каждой случайной величине соответствует некоторое множество возможных значений.
Примеры: 1) Опыт — бросание игрального кубика. СВ — число выпавших очков на верхней грани. Возможные значения: 1,2,3,4,5,6.
2) Покупается n лотерейных билетов. СВ – число выигрышей. Возможные значения: 0,1,2,…,n
3) Электрическая лампочка испытывается на длительность горения. СВ – длительность горения лампочки. Возможные значения: любое неотрицательное число.
4) Некто приходит на станцию метро и ожидает поезда. СВ – время ожидания ближайшего поезда. Возможные значения: [0;2мин].
Из примеров видно, что СВ различаются по множеству возможных значений.
Случайная величина называется дискретной(ДСВ), если множество её возможных значений счетно (в частности конечно), то есть может быть занумеровано. Примеры 1, 2 – ДСВ.
Случайная величина называется непрерывной (НСВ), если её возможные значения сплошь заполняют некоторый промежуток (или несколько промежутков) числовой оси. Примеры 3, 4 – НСВ. Различные СВ могут иметь одно и то же множество возможных значений. Поэтому для полного описания СВ необходимо знать, как часто СВ принимает то или иное свое значение.
2. Законы распределения СВ.
Законом распределения СВ называется всякое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.
Закон распределения ДСВ.
Для ДСВ закон распределения можно задать таблично, аналитически и графически.
1) Табличный способ – это таблица, в которой перечислены в порядке возрастания все возможные значения СВ и соответствующие вероятности принятия этих значений.
| ||||||||||||
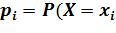 ) ) |
Эта таблица называется ряд распределения ДСВ.
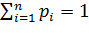
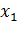
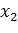
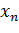
Если множество возможных значений случайной величины бесконечно (но счетно), то ряд 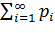
Опыт — бросание игрального кубика. СВ — число выпавших очков на верхней грани. Ряд распределения:
| хi | ||||||
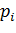 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
2) Аналитический способ – задаётся формула, по которой находится вероятность каждого возможного значения случайной величины.
Например, если опыт проводится по схеме Бернулли, то вероятности возможных значений могут быть найдены по формуле:
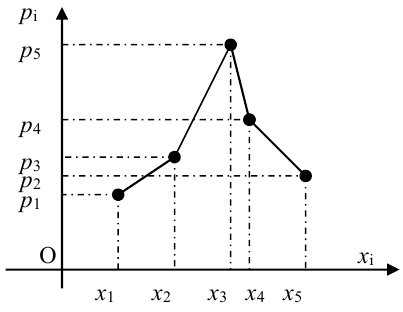
3) Графический способ.
Закон распределения можно изобразить графически, если по оси абсцисс откладывать значения СВ, а по оси ординат – их вероятности. Соединив точки (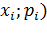
Закон распределения НСВ.
Под законом распределения НСВ понимают задание функции f(x), называемой плотностью распределения вероятности, такой, что вероятность попадания СВ в промежуток [a;b] равна P(a≤X≤b)=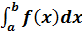
Свойства плотности вероятности:
1) f(x)≥0 (следует из аксиом вероятности);
2) 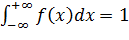
3) P(X=a)= 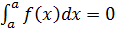
P(a ≤ X ≤ b) = P(a 
4) F(x) – неубывающая функция;
F(x)=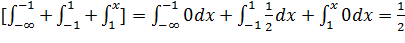
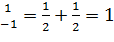
4. Операции над СВ.
Введём математические операции над ДСВ. Для НСВ вводится аналогично.
Пусть X — ДСВ, принимающая возможные значения 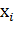
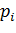
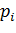
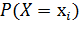
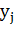
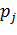
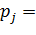
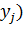
Произведением ДСВ X и постоянной величины С, называется ДСВ С∙Х, которая принимает возможные значения C∙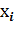
Суммой двух ДСВ X и Y называется ДСВ X+Y, которая принимает возможные значения 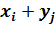
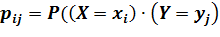
Произведением двух ДСВ X и Y называется ДСВ X∙Y, которая принимает возможные значения 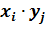
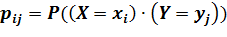
Две СВ называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая случайная величина.
Для независимых СВ X и Y выполняется:
Пусть дана ДСВ Х и функция φ(x), определенная на всей вещественной оси, тогда функцией от ДСВ Х называется ДСВ Y= φ(Х), которая принимает возможные значения 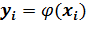
(где сумма по всем k таким, что значения φ(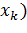
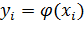
Пример: пусть даны дискретные случайные величины
| 0,4 | 0,6 |
| -1 | |
| 0,3 | 0,7 |
Тогда ДСВ 5X будет иметь ряд распределения:
Источник
Случайные величины — определение и вычисление с примерами решения
Содержание:
Величина называется случайной, если она принимает свои значения в зависимости от исходов некоторого испытания (опыта), причем для каждого элементарного исхода она имеет единственное значение. Случайная величина называется дискретной (в узком смысле), если множество всех возможных значений ее конечно.
Геометрически множество всех возможных значений дискретной случайной величины представляет конечную систему точек числовой оси.
Пусть X — дискретная случайная величина, возможными и единственно возможными значениями которой являются числа
вероятности этих значений (т. е. 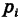
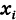
События 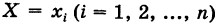
Определение: Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины.
В простейших случаях закон распределения дискретной случайной величины X удобно задавать таблицей:
Здесь первая строка таблицы содержит все возможные значения случайной величины, а вторая — их вероятности.
Заметим, что таблицу значений дискретной случайной величины X, если это целесообразно, формально всегда можно пополнить конечным набором любых чисел, считая их значениями X с вероятностями, равными нулю.
Пример:
В денежной лотерее разыгрывается 1 выигрыш в 1000 руб., 10 выигрышей по 100 руб. и 100 выигрышей по 1 руб. при общем числе билетов 10 000. Найти закон распределения случайного выигрыша X для владельца одного лотерейного билета.
Решение:
Здесь возможные значения для X есть
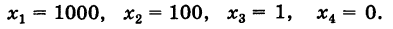
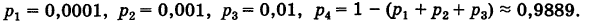
Число появлений т события А при 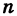
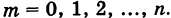
где 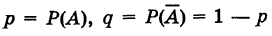
В частности, если р мало и п велико, причем 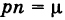
Определение случайной величины
Определение 29. Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.
Случайные величины (СВ) обозначаются большими буквами X, Y.
Примеры СВ: X — число попаданий при трех выстрелах, Y — абсцисса точки попадания при выстреле.
Случайные величины характеризуются своими возможными значениями, которые обозначаются маленькими буквами, соответствующими случайной величине: х,у.
Например, случайная величина X — число попаданий при трех выстрелах характеризуется следующими возможными значениями: 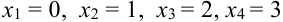
Определение 30. Случайные величины, принимающие только отдаленные друг от друга возможные значения, которые можно заранее перечислить, называются дискретными случайными величинами (ДСВ).
Примеры ДСВ. 1) В приведенном выше примере СВ X. 2) Случайная величина Z- число вызовов скорой помощи за сутки. Ее возможные значения 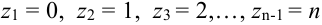
Определение 31. Случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток (который иногда имеет резко выраженные границы, а чаще — расплывчатые, неопределенные), называются непрерывными случайными величинами (НСВ).
Примеры НСВ. 1) В приведенном выше примере СНВ Y — абсцисса точки попадания при выстреле. Ее возможные значения заполняют некоторый промежуток 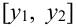
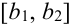
Замечание. В классической теории вероятностей рассматриваются события, в современной теории вероятностей — случайные величины.
Определение 32. Случайная величина X называется характеристической случайной величиной события А.
Примеры перехода от событий к случайным величинам
1). Рассмотрим событие А, которое в результате опыта происходит или нет. Введем в рассмотрение случайную величину X такую, что если А происходит, то Х= 1, если А не происходит, то Х=0. Следовательно, Х — дискретная случайная величина с возможными значениями 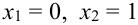
Если происходит ряд таких опытов, то общее число появлений события А равно сумме характеристических случайных величин X события А во всех опытах.
2). Пусть в действительности точка М совпадает с началом координат — точкой О. При измерении координат точки М были допущены ошибки. Событие А = <Ошибка в положении точки М не превзойдет заданного значения r>. Пусть X, Y — случайные ошибки при измерении координат точки. Это непрерывные случайные величины, так как их возможные значения непрерывно заполняют некоторые промежутки. Событие А равносильно попаданию точки M(X,Y) в пределы круга радиуса r с центром в точке О. Т.е. для выполнения события А случайные величины должны удовлетворять неравенству: 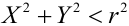
Законы распределения случайных величин
Для описания случайной величины (т.е. для возможности сказать, как часто следует ожидать появления тех или других возможных значений случайной величины в результате повторения опыта в одних и тех же условиях) необходимо знать закон распределения вероятностей случайной величины.
Определение 33. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Рассмотрим дискретную случайную величину (ДСВ) Xс возможными значениями 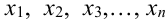
В результате опыта величина X примет одно из этих значений, т.е. произойдет одно из полной группы несовместных событий: X = 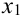
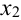
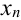
Обозначим 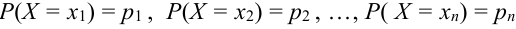
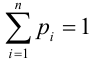
Эта суммарная вероятность каким-то образом распределена между отдельными значениями ДСВ. Задать это распределение, т.е. указать, какой вероятностью обладает каждое из событий, значит установить закон распределения СВ.
Говорят, что СВ подчинена данному закону распределения.
Формы закона распределения ДСВ
1. Простейшей формой задания закона распределения является таблица, называемая рядом распределения ДСВ.
Для элементов нижней строки должно выполняться условие: 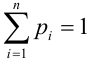
2. Формой задания закона распределения является многоугольник распределения — фигура, получаемая при графическом изображении ряда распределения.
Механическая интерпретация ряда распределения ДСВ: Распределение единичной массы в нескольких изолированных точках по оси (Ох). (В отдельных точках 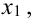

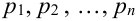
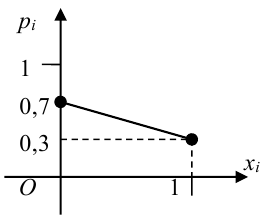
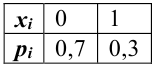
Пример №1
Рассмотрим опыт, в котором может появиться или не появиться событие А. Р(А) = 0,3. Рассмотрим случайную величину X — число появлений события А в данном опыте, т.е. возможные значения данной величины: 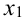
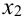
Решение.
Проверка: 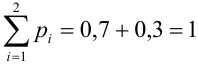
Пример №2
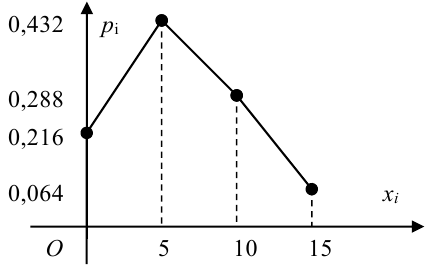
Стрелок производит 3 выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. За каждое попадание стрелку засчитывастся 5 очков. Построить ряд и многоугольник распределения числа выбитых очков.
Решение.
ДСВ X — число выбитых очков. Вероятность попадания (успеха) равна р = 0,4, вероятность промаха (неудачи) равна q = 1 — 0,4 = 0,6. Количество испытаний n = 3.
Возможные значения X: 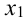
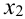
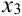
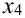
По формуле Бернулли 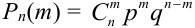
Ряд распределения имеет вид:
Проверка: 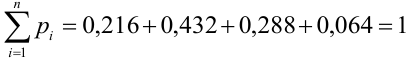
Замечание. Ряд распределения является удобной формой представления закона распределения для ДСВ с конечным числом возможных значений. Однако эта характеристика не универсальна, так как ряд или многоугольник нельзя построить для непрерывной случайной величины (НСВ). Действительно, НСВ имеет бесчисленное множество возможных значений, которые сплошь заполняют некоторый промежуток, и перечислить их в какой-нибудь таблице нельзя.
Кроме того (это будет доказано позднее) каждое отдельное значение НСВ обычно не обладает никакой отличной от нуля вероятностью. Следовательно, для НСВ не существует ряда распределения в том смысле, в каком он существует для ДСВ.
Однако различные области возможных значений НСВ все же не являются одинаково вероятными, и для НСВ существует «распределение вероятностей», хотя и не в том смысле, как для ДСВ.
В силу этого, желательно иметь такую характеристику распределения вероятностей, которая была бы применима для самых разнообразных случайных величин.
Пример №3
Вероятности того, что студент сдаст экзамены в сессию по математическому анализу и органической химии соответственно равны 0,7 и 0,8. Составить закон распределения случайной величины Х − числа экзаменов, которые сдаст студент.
Решение. Рассматриваемая случайная величина X в результате экзамена может принять одно из следующих значений:
Найдем вероятности этих значений. Обозначим события:
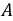
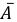
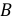
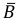
По условию:
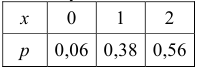
Итак, закон распределения случайной величины Х задается таблицей:
Пример №4
Дискретная случайная величина Х задана законом распределения:
Найти 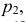
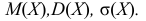
Решение: Так как сумма вероятностей возможных значений случайной величины Х равна 1, то 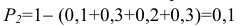
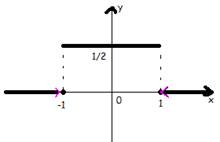
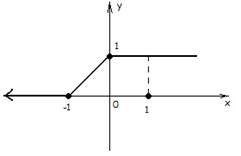
Найдем функцию распределения 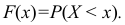
Геометрически это равенство можно истолковать так: F(х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Если 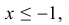
Если 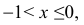
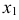
Если 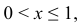
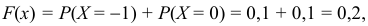
Если 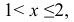
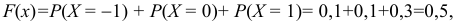
Если 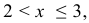
=0,1+0,1+0,3+0,2=0,7, так как в промежуток (−∞; х) попадают четыре значения
Если 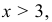
=0,1+0,1+0,3+0,2+0,3=1, так как в промежуток (−∞; х) попадают пять значений 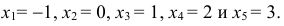
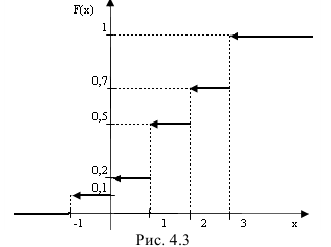
Итак,
Изобразим функцию F(x) графически (рис. 4.3):
Найдем числовые характеристики случайной величины:
Пример №5
Составить закон распределения случайной величины Х − числа выпадений пятерки при трех бросаниях игральной кости. Вычислить 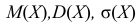
Решение: Испытание состоит в одном бросании игральной кости. Так как кость бросается 3 раза, то число испытаний n = 3.
Вероятность события А − «выпадение пятёрки» в каждом испытании одна и та же и равна 1/6, т.е. 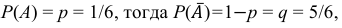
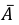
Случайная величина Х может принимать значения: 0;1;2;3.
Вероятность каждого из возможных значений Х найдём по формуле Бернулли:
Таким образом закон распределения случайной величины Х имеет вид:
Контроль: 125/216+75/216+15/216+1/216=1.
Найдем числовые характеристики случайной величины Х:
Пример №6
Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной равна 0,002. Найти вероятность того, что среди 1000 отобранных деталей окажется:
а) 5 бракованных;
б) хотя бы одна бракованная.
Решение: Число n = 1000 велико, вероятность изготовления бракованной детали р = 0,002 мала, и рассматриваемые события (деталь окажется бракованной) независимы, поэтому имеет место формула Пуассона:
Найдем 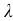
а) Найдем вероятность того, что будет 5 бракованных деталей среди отобранных (m = 5): 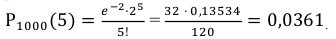
б) Найдем вероятность того, что будет хотя бы одна бракованная деталь среди отобранных.
Событие А − «хотя бы одна из отобранных деталей бракованная» является противоположным событию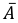
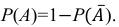
Математическое ожидание
Определение: Математическим ожиданием дискретной случайной величины называется сумма парных произведений всех возможных ее значений на их вероятности.
Если 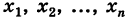
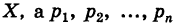
Очевидно, математическое ожидание случайной величины X не изменится, если таблицу значений ее пополнить конечным числом любых чисел, считая, что вероятности этих чисел равны нулю.
Математическое ожидание М (X) случайной величины есть величина постоянная и поэтому представляет числовую характеристику случайной величины X.
Пример №7
Найти математическое ожидание выигрыша X.
Решение:
Пользуясь помещенной там таблицей, имеем
Как нетрудно сообразить, М(Х) = 21 коп. есть «справедливая» цена билета.
Замечание 1. Отдельные слагаемые 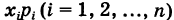
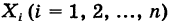
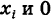
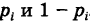
Замечание 2. Пусть 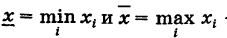
Таким образом, математическое ожидание случайной величины является некоторым ее средним значением.
Замечание 3. Математическое ожидание числа появлений события А при одном испытании совпадает с вероятностью этого события Р(А) = р.
Действительно, пусть X — число появлений события А в данном испытании. Случайная величина X может принимать два значения: 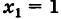
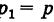
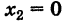
Основные свойства математического ожидания
Укажем важнейшие свойства математического ожидания. Доказательства будут проведены для дискретных случайных величин. Однако соответствующие теоремы справедливы также и для непрерывных случайных величин, поэтому при формулировках этих теорем мы не будем упоминать, что рассматриваемые случайные величины дискретны.
Нам понадобится выяснить смысл арифметических операций 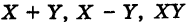
Например, под суммой X + У понимается случайная величина Z, значениями которой являются допустимые суммы 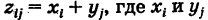
Если какая-нибудь из комбинаций 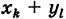
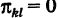
Аналогично определяются остальные выражения.
Различают также независимые и зависимые случайные величины. Две случайные величины считаются независимыми, если возможные значения и закон распределения каждой из них один и тот же при любом выборе допустимых значений другой. В противном случае они называются зависимыми. Несколько случайных величин называются взаимно независимыми, если возможные значения и законы распределения любой из них не зависят от того, какие возможные значения приняли остальные случайные величины.
Теорема: Математическое ожидание постоянной величины равно этой постоянной, т. е. если С — постоянная величина, то
Доказательство: Постоянную величину С можно рассматривать как случайную дискретную величину, принимающую лишь одно возможное значение С с вероятностью р = 1. Поэтому
Теорема: Математическое ожидание суммы двух (или нескольких) случайных величин равно сумме математических ожиданий этих величин, т. е. если X и У — случайные величины, то
Доказательство: 1) Пусть случайная величина X принимает значения 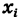
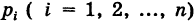
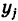
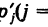
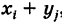
Как было отмечено выше, все комбинации 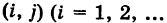
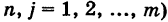
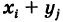
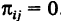
Воспользовавшись очевидными свойствами суммы: 1) сумма не зависит от порядка слагаемых и 2) множитель, не зависящий от индекса суммирования, можно выносить за знак суммы, из (4) получим
Сумма 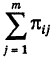
Тогда из формулы (5) получаем
что и требовалось доказать.
2) Для нескольких случайных величин, например для трех X, У и Z, имеем
Следствие. Если С — постоянная величина, то
Теорема: Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т. е.
где X и У — независимые случайные величины.
Доказательство: Пусть 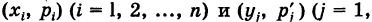
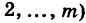
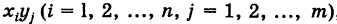
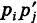
что и требовалось доказать.
Следствие 1. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин.
Действительно, например, для трех взаимно независимых случайных величин X, У, Z имеем
Следствие 2. Постоянный множитель можно выносить за знак математического ожидания.
Если С — постоянная величина, а X — любая случайная величина, то, учитывая, что С и X независимы, на основании теоремы 1 получим
Следствие 3. Математическое ожидание разности любых двух случайных величин X и Y равно разности математических ожиданий этих величину т. е.
Действительно, используя теорему о сумме математических ожиданий и следствие 2, получим
Дисперсия
Пусть X — случайная величина, М(Х) — ее математическое ожидание (среднее значение). Случайную величину X — М(Х) называют отклонением.
Теорема: Для любой случайной величины X математическое ожидание ее отклонения равно нулю, т. е.
Локазательство. Действительно, учитывая, что М(Х) — постоянная величина, имеем
Определение: Дисперсией (рассеянием) случайной величины называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания.
Отсюда, обозначая дисперсию буквой D, для случайной величины X будем иметь
Очевидно, что дисперсия случайной величины постоянна, т. е. является числовой характеристикой этой величины.
Если случайная величина X имеет закон распределения 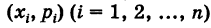
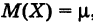
Пример №8
Пусть закон распределения случайной величины задан таблицей:
Определить математическое ожидание М(Х), дисперсию D(X) и среднее квадратичное отклонение 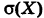
Дисперсия D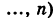
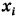
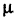
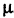
Теорема: Дисперсия случайной величины равна разности между математическим ожиданием квадрата этой величины и квадратом ее математического ожидания, т. е.
Доказательство: Используя основные теоремы о математических ожиданиях случайных величин, имеем
Теорема: Дисперсия постоянной величины равна нулю. Действительно, если С — постоянная величина, то М(С) = С и, следовательно,
Результат этот очевиден, так как постоянная величина изображается одной точкой на числовой оси Ох и не имеет рассеяния.
Теорема: Дисперсия суммы двух независимых случайных величин X и Y равна сумме дисперсий этих величин, т. е.
Доказательство: Так как
— так называемый корреляционный момент величин X и У. Если случайные величины X и У независимы, то случайные величины X — М(Х) и У — М(У), отличающиеся от X и У на постоянные величины, очевидно, также независимы. Поэтому в силу теорем 3 имеем
и, следовательно, справедлива формула (5).
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.
Следствие 2. Если С — постоянная величина, то
Таким образом, случайные величины X и X + С имеют одинаковую меру рассеяния.
Теорема: Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, т. е.
Доказательство: Если С — постоянный множитель, то в силу теоремы 2 имеем
Таким образом, рассеяние величины СХ в С 2 раз больше рассеяния величины X.
Следствие. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин, т. е. если случайные величины X и У независимы, то
Действительно, на основании теорем 4 и 5 имеем
Математическое ожидание и дисперсия случайной величины являются ее основными числовыми характеристиками.
Пример №9
Определить математическое ожидание и дисперсию для числа X появления события А при п независимых испытаниях, в каждом из которых вероятность события Р(А) = р постоянна.
Случайная величина X принимает значения 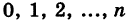
где
Величину X можно рассматривать как сумму независимых случайных величин
где 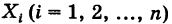
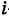
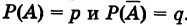
. Отсюда, используя теорему о математическом ожидании суммы, будем иметь
Таким образом, математическое ожидание числа появлений события А в условиях схемы Бернулли совпадает со «средним числом» появления этого события в данной серии испытаний. Для дисперсии случайной величины X, получаем
Отсюда по свойству дисперсии суммы независимых случайных величин (теорема) будем иметь
Поэтому среднее квадратичное отклонение (стандарт)
Формулы (8) и (9) дают математическое ожидание и дисперсию для биномиального закона распределения.
Замечание. Теперь становится понятным смысл случайной величины
в приближенных формулах Лапласа, а именно, t представляет собой отклонение числа появлений события А от его математического ожидания, измеренное в стандартах (так называемое нормированное отклонение).
Рассмотрим п дискретных попарно независимых случайных величин 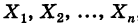
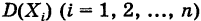
Эти величины, возможно, имеют значительный разброс, однако их среднее арифметическое
ведет себя достаточно «кучно».
А именно, при указанных выше условиях имеет место замечательная теорема:
Теорема Чебышева: Для любого положительного 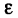
сколь угодно близка к 1, если число случайных величин п достаточно велико, т. е.
(закон .больших чисел в форме Чебышева).
Теорема Чебышева находит применение в теории ошибок, статистике и т. п.
Непрерывные случайные величины. Функция распределения
Случайную величину X будем называть непрерывной, если все ее возможные значения целиком заполняют некоторый конечный или бесконечный промежуток 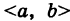
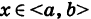
Для характеристики непрерывной случайной величины X вводят функцию распределения
называемую интегральным законом распределения.
Если значения случайной величины X рассматривать как точки числовой оси Ох, то Ф(х) представляет собой вероятность события, состоящего в том, что наблюдаемое значение случайной величины X принадлежит интервалу 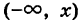
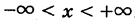
Заметим, что функция распределения имеет смысл также для дискретных случайных величин.
Функция распределения Ф(х) обладает следующими свойствами:
I.Функция Ф(х) есть неубывающая функция аргумента х, т. е. если 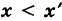
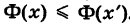
Действительно, если х’ > х, то из события 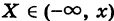
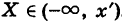
II.Так как Ф(х) — вероятность, то справедливо неравенство
III.
Действительно, событие 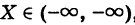
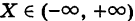
Зная функцию распределения Ф(х), можно для любого промежутка 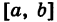
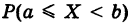
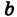
В самом деле, пусть А есть событие 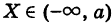
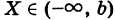
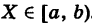
Тогда, очевидно, имеем
Так как события А и С несовместны, то по теореме сложения вероятностей получаем Р(Б) = Р(А) + Р(С), отсюда
причем 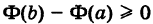
Таким образом, вероятность того, что случайная величина X примет значение, принадлежащее промежутку [a, b), равна приращению ее функции распределения на этом промежутке.
В дальнейшем случайную величину X будем называть непрерывной лишь в том случае, когда ее функция распределения Ф(х) непрерывна на оси 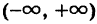
Теорема: Вероятность (до опыта) того, что непрерывная случайная величина X примет заранее указанное строго определенное значение а, равна нулю.
В самом деле, в силу формулы (2) имеем
Положим, что 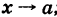
Переход я к пределу при 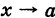
Таким образом, при непрерывной функции распределения вероятность «попадания в точку» равна нулю.
Следствие. Для непрерывной случайной величины X справедливы равенства
где 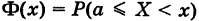
Аналогично доказывается второе равенство.
Замечание. В общем случае невозможные события и события с нулевой вероятностью могут оказаться неэквивалентными.
Предположим теперь, что для непрерывной случайной величины X ее функция распределения Ф(х) имеет непрерывную производную
Функцию ф(х) называют плотностью вероятности (для данного распределения) или дифференциальным законом распределения случайной величины X.
Термин плотность вероятности имеет следующий смысл. Пусть 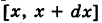
Заменяя бесконечно малое приращение функции 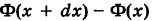
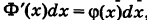
Таким образом, плотность вероятности представляет собой отношение вероятности попадания точки в бесконечно малый промежуток к длине этого промежутка.
Так как плотность вероятности ф(х) является производной неубывающей функции Ф(х), то она неотрицательна: 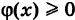
Так как Ф(х) является первообразной для ф(х), то на основании формулы Ньютона—Лейбница имеем
Отсюда в силу (3′) получаем
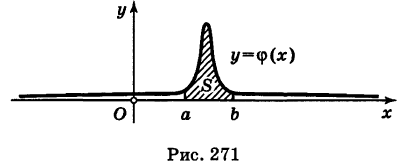
Геометрически (рис. 271) эта вероятность представляет собой площадь S криволинейной трапеции, ограниченной — графиком плотности вероятности у = ф(х), осью Ох и двумя ординатами
Полагая 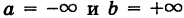
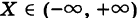
Полагая в формуле (6) 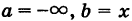
Числовые характеристики непрерывной случайной величины
Будем рассматривать бесконечно малый промежуток 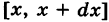
Представляя прямую 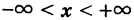
Определение: Под математическим о жид а ни ем непрерывной случайной величины X понимается число
(конечно, это определение имеет смысл лишь для таких случайных величин X, для которых интеграл (1) сходится).
Для дисперсии непрерывной случайной величины X сохраним прежнее определение
Из формулы (1) вытекает
(конечно, в предположении, что интеграл (2) сходится). Можно также пользоваться формулой
Можно доказать, что основные свойства математического ожидания и дисперсии дискретных случайных величин сохраняются также и для непрерывных случайных величин.
Пусть теперь все возможные значения непрерывной случайной величины X целиком заполняют конечный отрезок 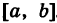
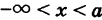
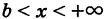
Равномерное распределение
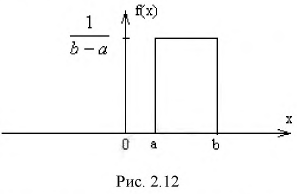
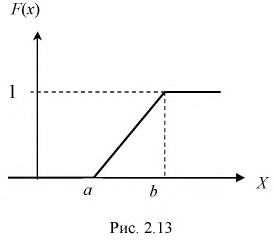
Непрерывная случайная величина X, все возможные значения которой заполняют конечный промежуток 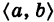
Иными словами, для равномерно распределенной случайной величины все ее возможные значения являются равновозможными.
Пусть, например, 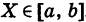
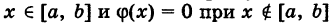
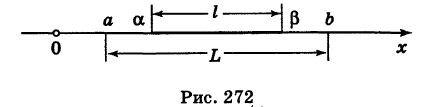
Пусть 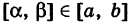
где L — длина (линейная мера) всего отрезка 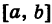
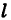
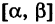
Значения случайной величины X, т. е. точки х отрезка 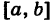
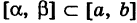
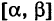
Согласно формуле (1) имеем геометрическое определение вероятности: под вероятностью события А понимается отношение меры 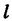
Это определение естественно переносит классическое определение вероятности на случай бесконечного числа элементарных исходов.
Аналогичное определение можно ввести также тогда, когда элементарные исходы испытания представляют собой точки плоскости или пространства.
Пример №10
В течение часа 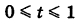
Решение:
Здесь множество всех элементарных исходов образует отрезок [0, 1], временная длина которого L = 1, а множество благоприятных элементарных исходов составляет отрезок [0,1/6] временной длины 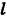
Поэтому искомая вероятность есть
Пример №11
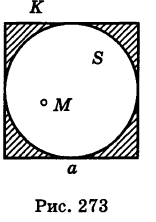
В квадрат К со стороной а с вписанным в него кругом S (рис. 273) случайно бросается материальная точка М. Какова вероятность того, что эта точка попадает в круг S?
Решение:
Здесь площадь квадрата есть К = а 2 , а площадь круга
За искомую вероятность естественно принять отношение
Эта вероятность, а следовательно, и число л, очевидно, могут быть определены экспериментально.
Нормальное распределение
Распределение вероятностей случайной величины X называется нормальным, если плотность вероятности подчиняется закону Гаусса
где 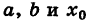
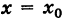
Для удобства выкладок эту кривую центрируем, введя новые координаты 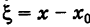
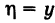
и будет представлять собой дифференциальный закон распределения случайной величины
Постоянные а и b в формуле (2) не являются произвольными, так как для плотности вероятностей 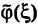
Делая замену переменной 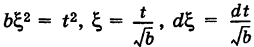
Отсюда на основании формулы (3) находим
Для математического ожидания случайной величины будем иметь
(ввиду нечетности подынтегральной функции). Отсюда
Таким образом, при нормальном распределении случайной величины X ее математическое ожидание х0 совпадает с точкой пересечения оси симметрии графика соответствующей кривой Гаусса с осью Ох (центр рассеивания).
Для дисперсии случайной величины X получаем
Полагая 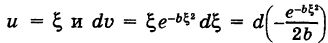
Таким образом, из формулы (9) получаем
Отсюда для среднего квадратичного отклонения величины X получим
Введя обозначение 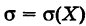
Подставляя эти значения в формулу (1), получим стандартный вид нормального закона распределения случайной величины X в дифференциальной форме:
где
Таким образом, нормальный закон распределения зависит только от двух параметров: математического ожидания и среднего квадратичного отклонения.
Нормальный закон распределения случайной величины в интегральной форме имеет вид
Формулы (11) и (12) упрощаются, если ввести нормированное отклонение
. Полагая в интеграле (12) 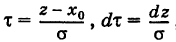
где t определяется формулой (13) и 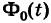
Отсюда получаем, что для случайной величины X, подчиняющейся нормальному закону, вероятность попадания ее на отрезок 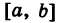
В частности, вероятность того, что отклонение величины X от ее математического ожидания х0 по абсолютной величине будет меньше а, равна
Полагая 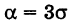
т. е. такое отклонение является почти достоверным (правило трех сигм).
Нормальный закон распределения вероятностей находит многочисленные применения в теории ошибок, теории стрельбы, физике и т. д.
Пример №12
Задана плотность распределения
Определить коэффициент к и функцию распределения
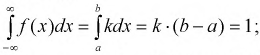
Построим график 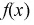
Найдем функцию распределения, используя (2.7):
Построим график 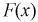
Функция распределения — универсальный закон распределения (для ДСВ и НСВ)
Для количественной характеристики распределения вероятностей любой случайной величины удобнее пользоваться не вероятностью события X = х, а вероятностью X 1) = 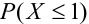
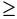
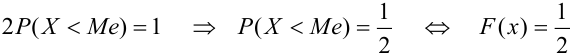
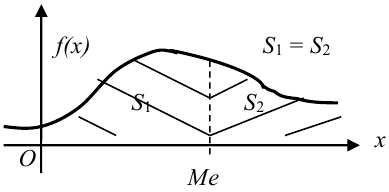
Таким образом, медиана — это корень уравнения 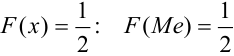
Геометрически: медиана — это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.
Замечание. В случае симметричного модального распределения медиана совпадает с мат. ожиданием и модой.
Когда медиана входит в формулы как определенное число, то ее обозначают 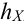
Моменты:
Данные характеристики описывают некоторые свойства распределения СВ. В механике, например, для описания распределения масс существуют статические моменты, моменты инерции.
Определение 43. Начальным моментом s — того порядка для ДСВ и НСВ называется математическое ожидание s — той степени этой случайной величины:
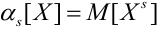
Замечание. При s = 1 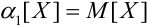
a) Для дискретных случайных величин: 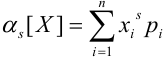
Замечание. Определение совпадает с определением начального момента порядка s в механике, если на оси (Ох) в точках 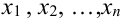
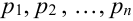
b) Для непрерывных случайных величин: 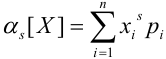
Определение 44. Центрированной случайной величиной, соответствующей величине X, называется отклонение случайной величины Х от ее математического ожидания:
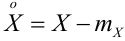
Рассмотрим математическое ожидание центрированной ДСВ:
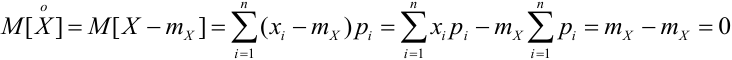
Аналогично, для НСВ 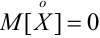
Центрирование СВ равносильно переносу начала координат в среднюю, центральную точку, абсцисса которой равна математическому ожиданию.
Определение 45. Моменты центрированной случайной величины называются центральными моментами.
Определение 46. Центральным моментом s — того порядка для ДСВ и НСВ называется математическое ожидание s — той степени соответствующей центрированной случайной величины:
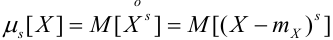
a) Для дискретных случайных величин: 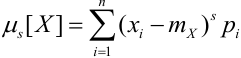
b) Для непрерывных случайных величин: 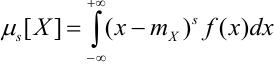
Замечание. Для любой СВ центральный момент 1-го порядка 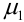
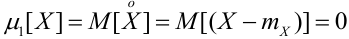
Рассмотрим подробнее центральные моменты 2, 3, 4 порядков и выведем соотношения, связывающие начальные и центральные моменты.
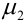
Определение 47. Дисперсией случайной величины X D[X] называется мат ожидание квадрата соответствующей центрированной случайной величины:
a) Для дискретных случайных величин: 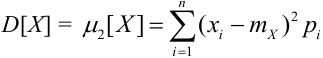
b) Для непрерывных случайных величин: 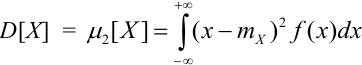
Дисперсия случайной величины — характеристика рассеивания, разбросанности значений случайной величины около ее мат. ожидания.
Когда дисперсия входит в формулы как определенное число, то ее обозначают
Механическая интерпретация D[X]: Дисперсия — момент инерции заданного распределения масс относительно центра тяжести (мат. ожидания).
Рассмотрим ДСВ. (Для НСВ получаем аналогично)
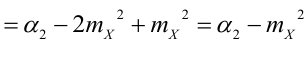
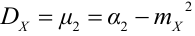
Свойства D[X].
1. D[C] = 0 , где С — постоянная.
2. 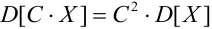
3. 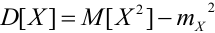
4. 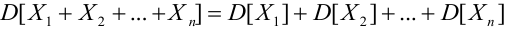
5. 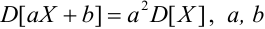
Замечание. D[X] имеет размерность квадрата случайной величины. Для более наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из D[X] извлекают корень:
где 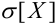
Когда среднее квадратическое входит в формулы как определенное число, то его обозначают 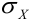
Замечание. Математическое ожидание и дисперсия характеризуют наиболее важные черты распределения: его положение и степень разбросанности. Для более подробного описания применяются моменты высших порядков.
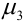
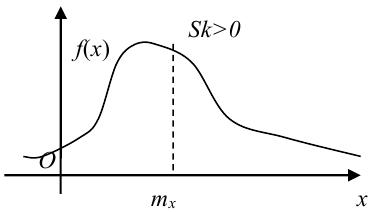
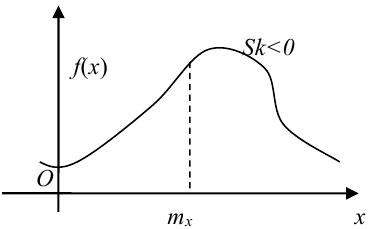
Асимметрия случайной величины — характеристика асимметрии или скошенности распределения значений случайной величины.
Теорема. Если распределение симметрично относительно мат. ожидания (т. е. масса распределена симметрично относительно центра тяжести), то все моменты нечетного порядка (если они существуют) равны нулю.
Доказательство.
Действительно, для ДСВ в сумме 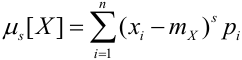
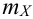
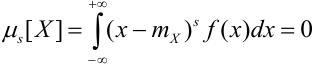
В связи с этим, в качестве характеристики асимметрии и выбирают простейший нечетный момент — третий 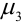
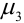
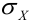
Определение 48. Коэффициентом асимметрии Sk случайной величины X называется величина
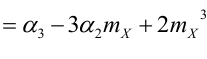
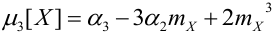
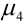
Четвертый центральный момент 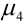
Это свойство описывается с помощью эксцесса.
Определение 49. Эксцессом случайной величины X называется величина
Число 3 вычитается из соотношения 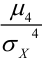
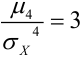
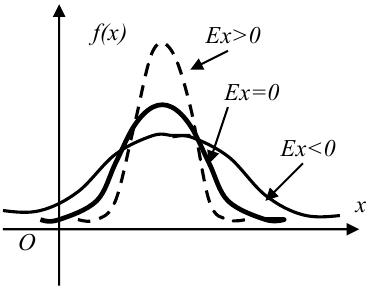
Кривая нормального распределения, для которого эксцесс равен нулю, принята как бы за эталон, с которым сравниваются другие распределения. Кривые более островершинные имеют положительный эксцесс, более плосковершинные — отрицательный.
Абсолютные моменты:
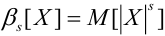
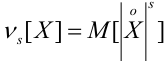
Абсолютные моменты четных порядков совпадают с обычными моментами. Из абсолютных моментов нечетного порядка чаще всего применяется первый абсолютный центральный момент:
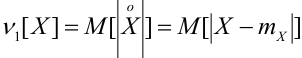
a) Для дискретных случайных величин: 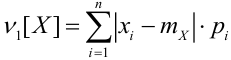
b) Для непрерывных случайных величин: 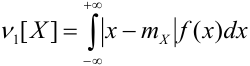
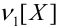
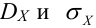
Замечания.
1. Моменты могут рассматриваться не только относительно начала координат (начальные) или математического ожидания (центральные), но и относительно произвольной точки а:
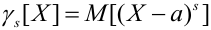
2. Во многих задачах полная характеристика случайной величины (закон распределения) не нужна или не может быть получена, поэтому ограничиваются приблизительным описанием СВ с помощью числовых характеристик, каждая из которых выражает какое-либо характерное свойство распределения. Иногда характеристиками пользуются для приближенной замены одного распределения другим.
Пример №17
Дан ряд распределения ДСВ:
Найти: 1) величину а, 2) математическое ожидание и дисперсию М[Х] и D[X] , 3) М[3Х + 2], D[2X + 3].
Решение.
1) Величину а найдем из условия: 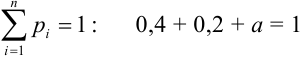
2) Найдем математическое ожидание и дисперсию:
По формуле (1) 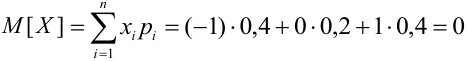
По формуле (8) 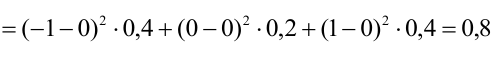
Дисперсию можно было найти, используя формулу (10) и (4):
3) М[ЗХ + 2] = (по 5 свойству мат. ожидания) = 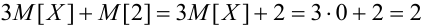
D[2X + 3] = (по 5 свойству дисперсии) =
Пример №18
Стрелок производит 3 выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,4. СВ Х — число попаданий. Определить: 1) математическое ожидание, 2) дисперсию, 3) среднее квадратическое отклонение, 4) моду, 5) асимметрию, 6) среднее арифметическое отклонение.
Решение.
Ранее мы построили ряд распределения числа попаданий. Ряд распределения имеет вид:
1) 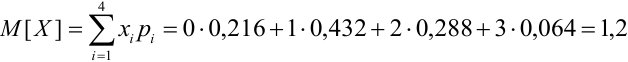
2) 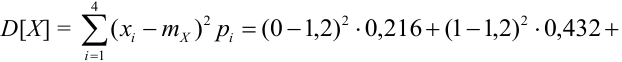
(по формуле 8. Можно было по формуле (4): 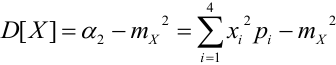
3) 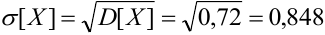
4) Найдем моду М: 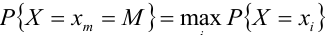
Тогда коэффициент асимметрии по формуле (12) 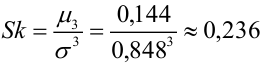
6) По формуле (14) найдем среднее арифметическое отклонение: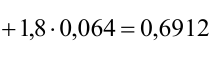
Пример №19
Непрерывная случайная величина подчинена закону распределения с плотностью 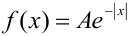
Решение.
1) Если х 2, то f(x) = 0 и, следовательно 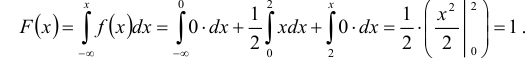
Пример №61
Методом произведений вычислить выборочную среднюю и выборочную дисперсию по данным выборки (табл. 3.1).
Решение. В качестве «ложного нуля» возьмем варианту 16.
Следовательно
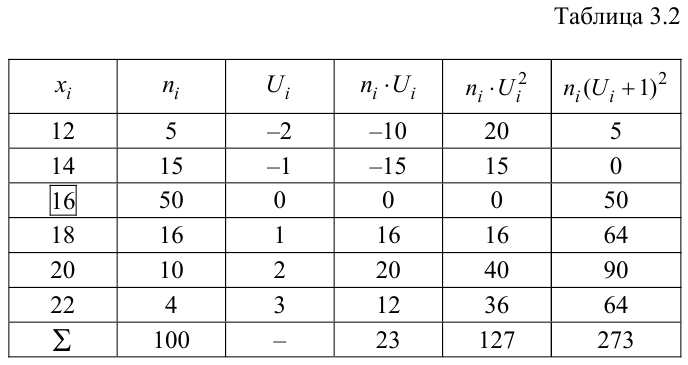
Результаты вычислений сведем в табл. 3.2.
Контроль: 273 = 100 + 46 + 127.
Равенство выполнено, следовательно, таблица заполнена верно.
Вычислим условные начальные моменты:
Вычислим выборочную среднюю и выборочную дисперсию:
Определим исправленную выборочную дисперсию:
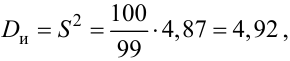
Получим несмещенные оценки для математического ожидания, дисперсии и среднего квадратического отклонения.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Числовые характеристики случайных величин
- Нормальный закон распределения
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Теоремы сложения и умножения вероятностей
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник