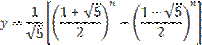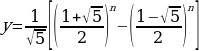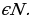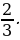Способы задания числовой последовательности
Методические указания
Определение 1.Функцию y = f(x), x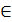 
N называют функцией натурального аргумента или числовой последовательностью и обозначают: y = f(n) или y1, y2, y3, . yn, . или (yn).
В данном случае независимая переменная – натуральное число.
Способы задания числовой последовательности
Правила задания последовательности описываются словами, без указания формул или когда закономерности между элементами последовательности нет.
Пример 1.Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, . .
Пример 2. Произвольный набор чисел: 1, 4, 12, 25, 26, 33, 39, . .
Пример 3. Последовательность чётных чисел 2, 4, 6, 8, 10, 12, 14, 16, .
Любой n-й элемент последовательности можно определить с помощью формулы.
Пример 1. Последовательность чётных чисел: y = 2n.
Пример 2.Последовательность квадрата натуральных чисел: y = n 2 ;
1, 4, 9, 16, 25, . n 2 , . .
Пример 3. Стационарная последовательность: y = C; C, C, C, . C, .
Частный случай: y = 5; 5, 5, 5, . 5, . .
Пример 4. Последовательность y = 2 n ;
2, 2 2 , 2 3 , 2 4 , . 2 n , . .
Указывается правило, позволяющее вычислить n-й элемент последовательности, если известны её предыдущие элементы.
Пример 1. Арифметическая прогрессия: a1=a, an+1=an+d, где a и d – заданные числа, d — разность арифметической прогрессии. Пусть a1=5, d=0,7, тогда арифметическая прогрессия будет иметь вид: 5; 5,7; 6,4; 7,1; 7,8; 8,5; . .
Пример 2. Геометрическая прогрессия: b1= b, bn+1= bnq, где b и q – заданные числа, b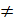 
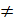
0, q 0; q – знаменатель геометрической прогрессии. Пусть b1=23, q=½, тогда геометрическая прогрессия будет иметь вид: 23; 11,5; 5,75; 2,875; . .
Пример 3. Последовательность Фибоначчи. Эта последовательность легко задаётся рекуррентно: y1=1, y2=1,yn-2+yn-1, если n=3, 4, 5, 6, . . Она будет иметь вид: 1, 1,2, 3, 5, 8, 13, 21, 34, 55, . .
Аналитически последовательность Фибоначчи задать трудно, но возможно. Формула, по которой определяется любой элемент этой последовательности, выглядит так:
Пример 1. Составить возможную формулу n-го элемента последовательности (yn):
а) Это последовательность нечётных чисел. Аналитически эту последовательность можно задать формулой y = 2n+1.
б) Это числовая последовательность, у которой последующий элемент больше предыдущего на 4. Аналитически эту последовательность можно задать формулой y = 4n.
Пример 2. Выписать первые десять элементов последовательности, заданной рекуррентно: y1=1, y2=2, yn = yn-2+yn-1, если n = 3, 4, 5, 6, . .
Каждый последующий элемент этой последовательности равен сумме двух предыдущих элементов.
Пример 3. Последовательность (yn) задана рекуррентно: y1=1, y2=2,yn=5yn-1— 6yn-2. Задать эту последовательность аналитически.
Найдём несколько первых элементов последовательности.
Получаем последовательность: 1; 2; 4; 8; 16; 32; 64; . которую можно представить в виде
2 0 ; 2 1 ; 2 2 ; 2 3 ; 2 4 ; 2 5 ; 2 6 . .
n = 1; 2; 3; 4; 5; 6; 7. .
Анализируя последовательность, получаем следующую закономерность: y = 2 n -1 .
Источник
Лекция по теме: «Числовая последовательность и способы её задания»
ТО 207 на 01.11.21 г. законспектировать лекцию и выполнить задания!
Просмотр содержимого документа
«Лекция по теме: «Числовая последовательность и способы её задания»»
ТО 207 законспектировать и выполнить задания! Прислать на почту: [email protected]
Тема: Определение числовой последовательности и способы её задания.
— знать, что такое числовая последовательность;
— способы задания числовой последовательности;
— уметь различать различные способы задания числовых последовательностей.
Краткие теоретические и учебно-методические материалы по теме практической работы (законспектировать!)
Определение 1. Функцию y = f(x), x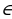 
N называют функцией натурального аргумента или числовой последовательностью и обозначают: y = f(n) или y1, y2, y3, . yn, . или (yn).
В данном случае независимая переменная – натуральное число.
Способы задания числовой последовательности.
Словесный способ: правила задания последовательности описываются словами, без указания формул или когда закономерности между элементами последовательности нет.
Пример 1. Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, . .
Пример 2. Произвольный набор чисел: 1, 4, 12, 25, 26, 33, 39, . .
Пример 3. Последовательность чётных чисел 2, 4, 6, 8, 10, 12, 14, 16, . .
Аналитический способ: любой n-й элемент последовательности можно определить с помощью формулы.
Пример 1. Последовательность чётных чисел: y = 2n.
Пример 2. Последовательность квадрата натуральных чисел: y = n 2
1, 4, 9, 16, 25, . n 2 , . .
Пример 3. Стационарная последовательность: y = C
Частный случай: y = 5; 5, 5, 5, . 5, . .
Пример 4. Последовательность y = 2 n
2, 2 2 , 2 3 , 2 4 , . 2 n , . .
Рекуррентный способ: указывается правило, позволяющее вычислить n-й элемент последовательности, если известны её предыдущие элементы.
Пример 2. Геометрическая прогрессия: b1= b, bn+1= bn q, где b и q – заданные числа, b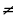 
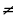
0, q 0; q – знаменатель геометрической прогрессии. Пусть b1=23, q=½, тогда геометрическая прогрессия будет иметь вид: 23; 11,5; 5,75; 2,875; . .
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, . .
Аналитически последовательность Фибоначчи задать трудно, но возможно. Формула, по которой определяется любой элемент этой последовательности, выглядит так:
Пример 1. Составить возможную формулу n-го элемента последовательности (yn):
а) Это последовательность нечётных чисел. Аналитически эту последовательность можно задать формулой y = 2n+1.
б) Это числовая последовательность, у которой последующий элемент больше предыдущего на 4. Аналитически эту последовательность можно задать формулой
Каждый последующий элемент этой последовательности равен сумме двух предыдущих элементов.
Найдём несколько первых элементов последовательности.
Получаем последовательность: 1; 2; 4; 8; 16; 32; 64; . которую можно представить в виде
2 0 ; 2 1 ; 2 2 ; 2 3 ; 2 4 ; 2 5 ; 2 6 . .
n = 1; 2; 3; 4; 5; 6; 7. .
Анализируя последовательность, получаем следующую закономерность: y = 2 n -1 .
а) Сколько в ней положительных членов?
б) Найти наибольший элемент последовательности.
в) Есть в данной последовательности наименьший элемент?
Данная числовая последовательность – это функция вида y = -5x 2 +24x+36, где x 
а) Найдём значения функции, при которых -5x 2 +24x+360. Решим уравнение -5x 2 +24x+36=0.
D = b 2 -4ac=1296,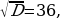 
X1=6, X2=-1,2.
Уравнение оси симметрии параболы y = -5x 2 +24x+36 можно найти по формуле x=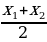 
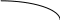
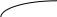
, получим: x=2,4.
Неравенство -5x 2 +24x+360 выполняется при -1,2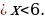 
В этом интервале находится пять натуральных чисел (1, 2, 3, 4, 5). Значит в заданной последовательности пять положительных элементов последовательности.
б) Наибольший элемент последовательности определяется методом подбора и он равен y2=64.
в) Наименьшего элемента нет.
Задания для практической работы:
Из двух вариантов практической работы выберите свой вариант. Это зависит от начальной букв фамилии: А-К (1 вариант), Л-Я (2 вариант. При замене одного варианта другим практическая работа считается невыполненной.
1. Составьте возможную формулу n-го элемента последовательности (yn), если последовательность имеет вид: 2, 4, 6, 8, 10, 12, . .
3. Найдите формулу n-го элемента и сумму первых 15 элементов арифметической прогрессии с первым элементом 3,4 и разностью 0,9.
4. Найдите сумму бесконечной геометрической прогрессии с первым членом 3,5 и знаменателем — 
5. В арифметической прогрессии a5= -150, a6= -147. Найдите номер первого положительного элемента этой последовательности.
6. Укажите наиболее близкий к нулю элемент арифметической прогрессии
а) Сколько в ней положительных элементов?
б) Найти наибольший элемент последовательности.
в) Есть в данной последовательности наименьший элемент?
1. Составьте возможную формулу n-го элемента последовательности (yn), если последовательность имеет вид: 7, 11, 15, 19, 23, . .
3. Найдите формулу n-го элемента и сумму первых 15 элементов арифметической прогрессии с первым элементом 3,5 и разностью 0,8.
4. Найдите сумму бесконечной геометрической прогрессии с первым членом 4,5 и знаменателем —
5. В арифметической прогрессии a5= 160, a6= 156. Найдите номер первого отрицательного элемента этой последовательности.
6. Укажите наиболее близкий к нулю элемент арифметической прогрессии
а) Сколько в ней положительных элементов?
б) Найти наибольший элемент последовательности.
в) Есть в данной последовательности наименьший элемент?
Источник
Гл. 8. Последовательности. Урок 2. Способы задания
Арифметическая и геометрическая прогрессии (14 часов)
Способы задания последовательностей, урок 2
Воспитательн а я
Создание условий для расширение понятийной базы за счет включения в нее новых элементов (понятия « словесный способ задания», «рекуррентный способ») ; формирование умений находить члены последовательности разными способами .
Ф ормировани е умений давать полные, математически грамотные ответы, развити е оперативной памяти, произвольного внимания, наглядно-действенного мышления.
Повышение коммуникативной активности учащихся, создание благоприятных условий для проявления индивидуальности, выбора своей позиции, формирование умения аргументировано отстаивать свою точку зрения, воспитание настойчивости, воли, характера учащихся для достижения конечного результата .
Планируемые результаты обучения , в том числе и формирование УУД:
Личностные: уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные: работа ют над понятием информация — знание; развива ют познавательную деятельность.
Предметные: понима ют , что такое числовая последовательность, какие бывают способы задания последовательности , уме ют использовать формулы для вычисления членов последовательности й , записи самой последовательности.
Универсальные учебные действия:
Познавательные УУД: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы.
Регулятивные УУД: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач.
Коммуникативные УУД : учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве; умеют работать в группе.
Личностные УУД: развивают способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Основные понятия: словесный способ, рекуррентная формула
Урок открытия новых знаний
Источники информации: учебник «Алгебра, 9 класс: учеб. для общеобраз. учреждений» Мордкович А.Г., М.: Просвещение, 2014 г.,
ТСО: ноутбук, мультимедиапроектор, экран
Средства наглядности: презентация « Способы задания последовательностей » , «Знаменитые последовательности»
Дидактические средства обучения: карточки-помощницы для слабоуспевающих учащихся
Цель этапа: подготовить учащихся к работе на уроке
Взаимное приветствие. Проверка готовности учащихся к уроку. Быстрое включение учащихся в деловой ритм . Правила дружной работы
Раппорт дежурного, фиксация отсутствующих
Актуализация опорных знаний учащихся
Цель этапа: подготовка учащихся к восприятию нового учебного материала, т.е. актуализация знаний и практических и умственных умений
Учитель: П роверим ваши логические способности. Я называю несколько слов, а вы должны продолжить:
а). П онедельник, вторник,…..
б). Я нварь, февраль, март…;
в). Акулич М., Байрангулов Р., Балышева А…..(список класса);
г). 10,11,12,…99 . (последовательность двузначных чисел)
Из ответов ребят делается вывод, что вышеназванные задания – это последовательности, то есть какой-то упорядоченный ряд чисел или понятий, когда каждое число или понятие стоит строго на своем месте, и, если поменять местами члены, то последовательность нарушится (вторник, четверг, понедельник – это просто перечисление дней недели).
1. Сформулируйте определение числовой последовательности.
2. Назовите способы задания числовой последовательности.
3. Приведите пример последовательности, заданной формулой n-го члена. Найдите пять первых членов этой последовательности.
Источник
