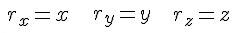Способы задания положения тела в пространстве
1. Описание движения с помощью параметров траектории.
Пусть траектория движения известна. Тогда, зная зависимость пути, пройденного телом, от времени, можно определить его положение в любой момент.
2. Векторный способ описания движения.
Положение тела в пространстве можно задать также в виде радиуса-вектора r. В произвольный момент времени оно определяется зависимостью r(t) . Вектор перемещения s(t) рассчитывается как разность между величинами радиуса-вектора r(t) в различные моменты времени t .
3.Координатный способ описания движения.
Поскольку векторная величина может быть представлена как сумма ее проекций, то положение тела в пространстве в любой момент времени можно определить, исходя из зависимостей от времени проекций радиуса-вектора на оси координат x(t), y(t), z(t).
3. Кинематика материальной точки: Путь, перемещение, траектория. Скорость (средний вектор скорости, мгновенная скорость). Проекции вектора скорости на оси координат. Равномерное движение.
Радиус-вектор –вектор, проведенный из начала координат в данную точку.
Траектория –линия, вдоль которой движется частица.
Путь –длина траектории.
Вектор перемещения –отрезок, поведенный из начального положения тела в конечное.
Скорость –быстрота изменения положения точки в пространстве.
1) Средняя – величина, равная проеденному пути ко времени, в течение которого продолжалось движение.
2) Мгновенная – величина, равная производной от радиуса-вектора точки по времени.
υ = lim ∆r/∆t, при ∆t→0 или υ=r’
Равноме́рное движе́ние — механическое движение, при котором тело за любые равные отрезки времени проходит одинаковое расстояние
4. Прямолинейное равнопеременное движение, его характеристики и их взаимосвязь.
Равнопеременное движение, движение точки, при котором её касательное ускорение wt (в случае прямолинейного Р. д. всё ускорение w) постоянно. Скорость v, которую имеет точка через t сек после начала движения, и её расстояние s от начального положения, измеренное вдоль дуги траектории, определяются при Р. д. равенствами:
где v0 — начальная скорость точки. Когда знаки v и wt одинаковы, Р. д. является ускоренным, а когда разные — замедленным.
5. Движение материальной точки при движении по криволинейной траектории, тангенциальное, нормальное и полное ускорения.
При неравномерном движении скорость частицы может меняться как по величине, так и по направлению. Быстрота изменения скорости определяется ускорением, которое равно первой производной от скорости по времени или второй производной от пути по времени.
Ускорение –изменение скорости тела со временем.
a= lim ∆υ/∆t=dυ/dt= υ’ при ∆t→0
a=d/dt*(dr/dt)=d 2 r/dt 2 =dr/dt=r’’
Быстрота поворота вектора скорости пропорциональна модулю скорости и кривизны траектории.
с=lim ∆φ/∆S=∆φ/∆S, при ∆S→0 ,
∆φ – угол между кривой и касательной
R=1/С – радиус кривизны
Тангенциальное ускорение – изменение величины вектора скорости точки со временем.
Нормальное ускорение-изменение направления вектора скорости материальной точки со временем.
an=a-aτ=(υ 2 /R)*n, где n-вектор нормали, перпендикулярный вектору τ, т.е(n, τ)=0, τ-единичный вектор направленный параллельно вектору скорости
R- радиус кривизны, где определяется скорость движения или радиус окружности касательной в данной точке к искривленной траектории движения.
6. Прямая и обратная задача кинематики. Поступательное и вращательное движение твердого тела.
Абсолютно твердое тело —тело деформациями которого можно пренебречь в данной задаче.
Поступательное движение – движение при котором любая прямая, жестко связанная с телом остается при своём движение параллельно самой себе.
Следовательно, для описания поступательного движения твердого тела достаточно знать, как движется одна из его точек.
Вращательное движение – движение тела, при котором все его точки движутся по окружности, центры которых лежат на одной прямой, называемой осью вращения, а плоскости окружности перпендикулярны оси вращения.
7. Кинематические характеристики вращательного движения, связь между угловыми и линейными характеристиками движения материальной точки.
Угловая скорость –это вектор ω, численно равный первой производной от угла поворота по времени, и направленный вдоль оси вращения в направлении dφ (ω и dφ всегда направлены в одну сторону).
ω=lim ∆φ/∆t=dφ /dt при ∆t→0
Угловая скорость направлена вдоль оси вращения в сторону, определяемую правилом правого винта. Как и угол поворота ∆φ, она является псевдовектором
При неравномерном вращении вектор угловой скорости может менять как свою величину, так и свое направление за счет поворота оси вращения.
Угловое ускорение –это вектор ε, второй производной от угла поворота по времени.
ε=lim ∆ω/∆t=dω/dt при ∆t→0
Угловое ускорение тоже является пседовектором, его размерность. Если e >0, то вектор направлен в ту же сторону, куда направлен и вектор. Если e
Источник
Способы задания положения тела пространстве
§ 7. Три способа задания положения точки в пространстве
1. Координатный способ.
Координаты определяют положение точки однозначно: например, M ( x , y , z ). Они являются числами, которые могут быть положительными, отрицательными или равными нулю.
2. Векторный способ задания положения точки на плоскости и в пространстве.
Определение. Радиус-вектором
некоторой точки пространства называется вектор, проведённый из начала координат в данную точку пространства.
Радиус-вектор также однозначно определяет положение точки в пространстве, так как он указывает, в каком направлении расположена точка, а модуль этого вектора указывает, на каком расстоянии находится точка от начала координат.
Проекции радиуса-вектора на оси координат равны координатам конца этого вектора (см. рис. выше).
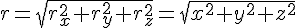
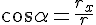
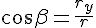
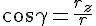
3. Естественный способ задания положения точки.
Он применяется тогда, когда известна траектория, по которой движется точка.
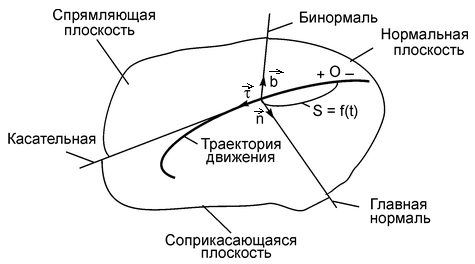
На траектории выбирают начало координат, а также положительное и отрицательное направление отсчёта дуговых координат. Векторные величины в этом случае проецируются на так называемые естественные оси координат: нормаль 
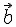
Начало естественных осей координат совмещают с той точкой траектории, через которую в данный момент проходит движущаяся точка. Касательную проводят в положительном направлении отсчёта дуг. Нормаль проводят перпендикулярно касательной и вовнутрь вогнутости траектории. Бинормаль направляют перпендикулярно плоскости, в которой расположены векторы 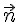
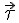
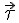
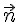
Никакую часть этого материала ни в каких целях, включая образовательные и научные, нельзя без письменного разрешения владельца авторских прав дублировать в сети Интернет и воспроизводить в какой бы то ни было форме и какими бы то ни было средствами, будь то электронные или механические, включая запись на магнитный или электронный носитель, вывод на печать, фотокопирование.
Источник
Способы задания положения тела пространстве
Способы задания положения тела в пространстве
1. Описание движения с помощью параметров траектории .
Пусть траектория движения известна. Тогда, зная зависимость пути, пройденного телом, от времени, можно определить его положение в любой момент.
Напомним, что путь ( L ) — это расстояние, пройденное телом вдоль траектории.
2. Векторный способ описания движения.
Положение тела в пространстве можно задать также в виде радиуса-вектора r . В произвольный момент времени оно определяется зависимостью r (t) . Вектор перемещения s (t) рассчитывается как разность между величинами радиуса-вектора r (t) в различные моменты времени t .
На рисунке тело в момент времени t 1 находилось в точке A , а в момент t 2 — в точке B .
Отметим, что путь всегда превосходит или равен величине вектора перемещения L(t) >= | s (t)| . Равенство достигается только в случае прямолинейного движения в одном направлении.
Поскольку векторная величина может быть представлена как сумма ее проекций, то положение тела в пространстве в любой момент времени можно определить, исходя из зависимостей от времени проекций радиуса-вектора на оси координат x(t), y(t), z(t) .
Пример. В качестве одного из примеров координатного способа можно привести описание движения тела, брошенного под углом a к горизонту. Движение по горизонтали происходит с постоянной скоростью, следовательно, x = V 0 ·sin( a )·t . Движение по горизонтали является равнопеременным с ускорением свободного падения g , следовательно, y = V 0 ·cos( a )·t — g·t 2 /2 . Исключив из этих уравнений время, получим, что траектория — зависимость y = f(x) представляет из себя параболу.
Действительно, движение ярких частиц по такой траектории мы можем наблюдать при извержении вулкана или салюте.
Источник
Способы задания положения точки и описание ее движения — Кинематика — МЕХАНИКА
1.1. Кинематика
1.1.5. Способы задания положения точки и описание ее движения
Положение точки в пространстве задается двумя способами:
1) с помощью координат; 2) с помощью радиус-вектора.
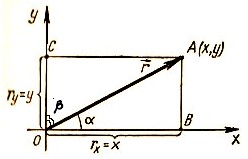
Положение точки с помощью координат задается тремя проекциями точки х, у, z на оси декартовой системы координат ОХ, ОУ, ОZ, связанные с телом отсчета (рис. 1.3). Для этого из точки А необходимо опустить перпендикуляры на плоскости УZ (координата х), ХZ (координата у), ХУ (координата z) соответственно. Записывается это так: А (х, у, z). Для конкретного случая, изображенного на рис. 1.3 (х = 6, у = 10, z = 4,5), точка А обозначается A (6; 10; 4,5).
Наоборот, если заданы конкретные значения координат точки в данной системе координат, то для изображения самой точки необходимо отложить значения координат на соответствующие оси (х на ось ОХ и т. д.) и на этих трех взаимно перпендикулярных отрезках построить параллелепипед. Вершина его, противоположная началу координат О и лежащая на диагонали параллелепипеда, и будет искомой точкой А.
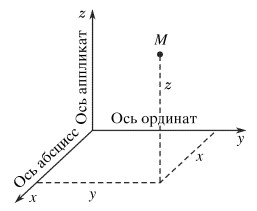
Если точка движется в пределах некоторой плоскости, то через выбранные на теле отсчета точки достаточно провести две координатные оси: ОХ и ОУ. Тогда положение точки на плоскости определяют двумя координатами х и у (рис. 1.4).
Если точка движется вдоль прямой, достаточно задать одну координатную ось ОХ и направить ее вдоль линии движения.
Задание положения точки А с помощью радиус-вектора осуществляется соединением точки А с началом координат О (рис. 1.4). Направленный отрезок О А = называется радиус-вектором.
Радиус-вектор — это вектор, соединяющий начало отсчета с положением точки в произвольный момент времени.
Точка задана радиус-вектором, если известны его длина (модуль) и направление в пространстве, т. е. значения его проекций rх, ry, rz на оси координат ОХ, ОУ, OZ, либо углы между радиус-вектором и осями координат. Для случая движения на плоскости (рис. 1.4) имеем:
Здесь r = | — модуль радиус-вектора , х и y — его проекции на оси координат, все три величины — скаляры; х и у — координаты точки А.
Последние уравнения демонстрируют связь между координатным и векторным способами задания положения точки.
Вектор г можно также разложить на составляющие по осям X и У, т. е. представить в виде суммы двух векторов (рис. 1.4):
Таким образом, положение точки в пространстве задается либо ее координатами, либо радиус- вектором.
Способы описания движения точки
В соответствии со способами задания координат движение точки можно описать: 1) координатным способом; 2) векторным способом.
При координатном способе описания (или задания) движения изменение координат точки со временем записывается в виде функций всех трех ее координат от времени:
Уравнения (1.1) называют кинематическими уравнениями движения точки, записанными в координатной форме. Зная кинематические уравнения движения и начальные условия (т. е. положение точки в начальный момент времени), можно определить положение точки в любой момент времени.
При векторном способе описания движения точки изменение ее положения со временем задается зависимостью радиус-вектора от времени:
Уравнение (1.2) представляет собой уравнение движения точки, записанное в векторной форме. Если оно известно, то для любого момента времени можно рассчитать радиус-вектор точки, т. е. определить ее положение (как и в случае координатного способа). Таким образом, задание трех скалярных уравнений (1.1) равносильно заданию одного векторного уравнения (1.2).
Для каждого случая движения вид уравнений (1.1) или (1.2) будет вполне определенным. Если траекторией движения точки является прямая линия, движение называетсяпрямолинейным, а если кривая — криволинейным.
Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.
Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.
Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.
Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.
© 2014-2021 Все права на дизайн сайта принадлежат С.Є.А.
Источник

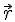 некоторой точки пространства называется вектор, проведённый из начала координат в данную точку пространства.
некоторой точки пространства называется вектор, проведённый из начала координат в данную точку пространства.