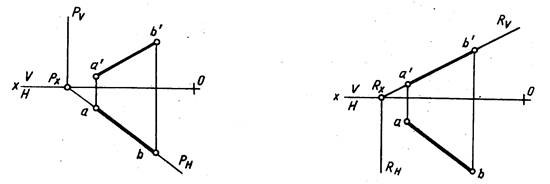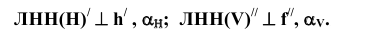СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТИ НА ЭПЮРЕ
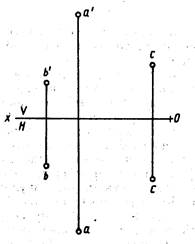
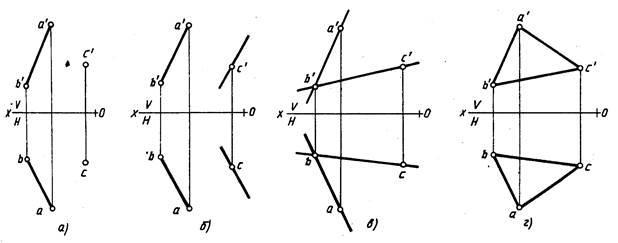
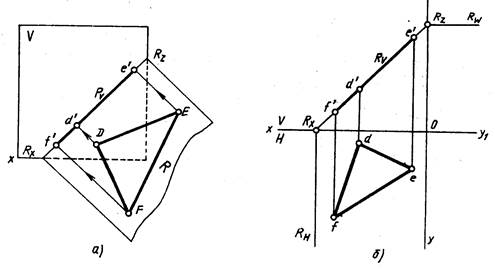
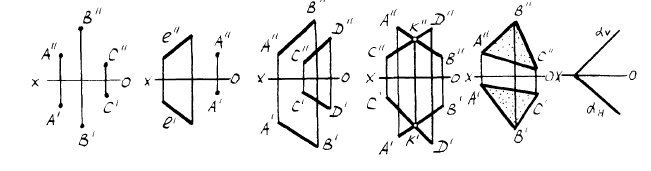
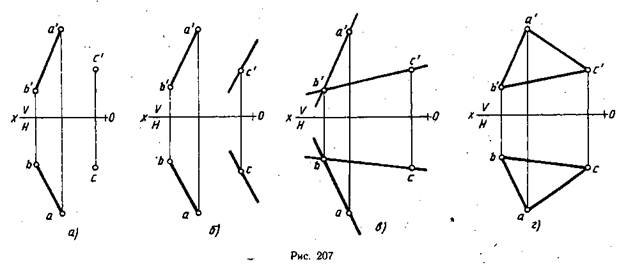
Положение плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой. Поэтому чтобы задать на эпюре плоскость, достаточно задать три ее точки (рис. 206). Плоскость можно задать точкой и прямой (рис. 207, а), двумя параллельными прямыми (рис. 207, б), двумя пересекающимися прямыми (рис. 207, в), треугольником (рис. 207, г).
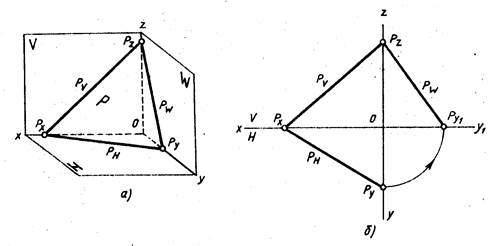
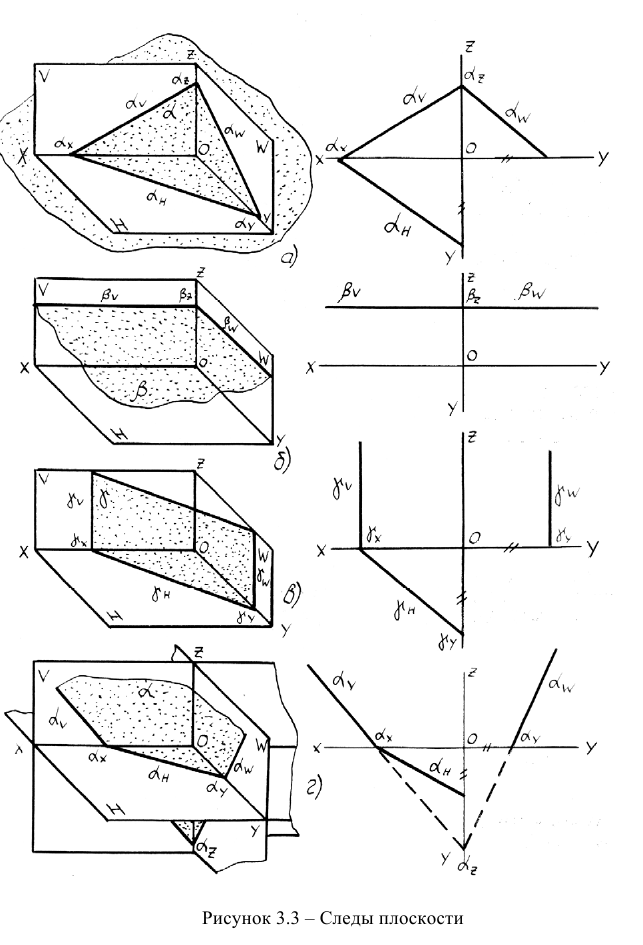
Можно задать плоскость следами. Следом плоскости называют прямую, по которой данная плоскость пересекает плоскость проекций. На рис. 208 Pv — фронтальный след плоскости Р, Рн — горизонтальный след плоскости Р, Pw — профильный след плоскости Р.
Различные случаи расположения плоскостей относительно плоскостей проекций
Плоскость общего положения — плоскость, расположенная наклонно ко всем плоскостям проекций (рис. 208). Такая плоскость пересекается с тремя плоскостями проекций по прямым, которые являются следами этой плоскости. Каждая пара следов сходится в точке, которая называется точкой схода следов плоскости и располагается на оси проекций. Плоскость общего положения имеет три точки схода, которые обозначаются Рх, Ру, Рz. В этих точках плоскость пересекает оси координат. Плоские фигуры, лежащие в плоскости общего положения, проецируются проекций с искажением.
Проецирующая плоскость — плоскость, перпендикулярная какой-либо плоскости проекций.
Горизонтально — проецирующая плоскость — плоскость, перпендикулярная горизонтальной плоскости проекций Н (рис. 209).
Фронтально — проецирующая плоскость — плоскость, перпендикулярная фронтальной плоскости проекции (рис. 210).
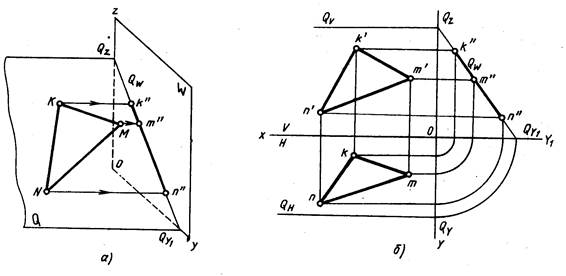
Профильно-проецирующая плоскость — плоскость, перпендикулярная профильной плоскости проекций (рис. 211).
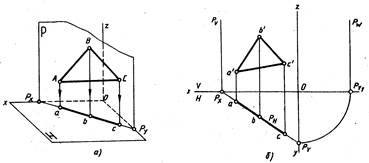
Проецирующая плоскость проецируется на плоскость проекций, к которой она перпендикулярна, в прямую. Па рис. 209 плоскость Р горизонтально-проецирующая, ΔАВС, лежащий в плоскости Р, проецируется в отрезок прямой линии, который совпадает со следом плоскости Рн. На рис. 210 ΔDEF, принадлежащий фронтально-проецирующей плоскости R, проецируется в отрезок, совпадающий со следом плоскости Rv. На рис. 211 ΔKMN, лежащий в профильно-проецирующей плоскости Q, проецируется на плоскость W в отрезок, совпадающий со следом плоскости Qw. Поэтому проецирующие плоскости часто используются в качестве вспомогательных при различных построениях. Например, чтобы через прямую AB провести горизонтально-проецирующую плоскость (рис. 212), достаточно через горизонтальную проекцию прямой ab провести горизонтальный след этой плоскости, так как все, что в этой плоскости лежит, в том числе и прямая AB, проецируется на ее горизонтальный след. Фронтальный след фронтально-проецирующей плоскости совпадает с фронтальной проекцией прямой a’b’ (рис. 213). Следы проецирующих плоскостей на других плоскостях проекций перпендикулярны соответствующим осям проекций (см. рис. 209, 210, 211).
Рис. 212 Рис. 213
Плоскости, перпендикулярные двум плоскостям проекций, параллельны третьей плоскости проекций. Геометрические фигуры, лежащие в этих плоскостях, проецируются без искажения на ту плоскость проекций, которой параллельна данная плоскость (рис. 214, 215; 216). Называются такие плоскости так же, как и плоскость проекций, параллельно которой они расположены: горизонтальная плоскость (рис. 214), фронтальная плоскость (рис. 215), профильная плоскость (рис. 216).
Источник
Плоскость на эпюре Монжа в начертательной геометрии с примерами
Плоскость на эпюре Монжа:
Плоскость на эпюре может быть задана шестью способами: тремя точками, не лежащих на одной прямой; прямой и точкой, не лежащей на прямой; двумя параллельными прямыми; двумя пересекающимися прямыми; любой плоской фигурой и следами (рисунок 3.1). 
Плоскости аналогично прямым делятся на плоскости общего и частного положения. На рисунке 3.2 представлены пространственные чертежи плоскостей.
У проецирующих плоскостей два следа всегда перпендикулярны осям. Третий след наклонен к соответствующей оси и называется собирательным следом. Он называется так потому, что, если в плоскости находится какой-либо геометрический объект (точка, прямая или кривая линия, треугольник и т.д.), то он проецируется на этот след в линию, совпадающую со следом (след «собирает» на себя проекцию объекта).
У плоскостей, параллельных плоскостям проекций, один след отсутствует, а два других следа являются продолжением друг друга и параллельны соответствующим осям проекций.
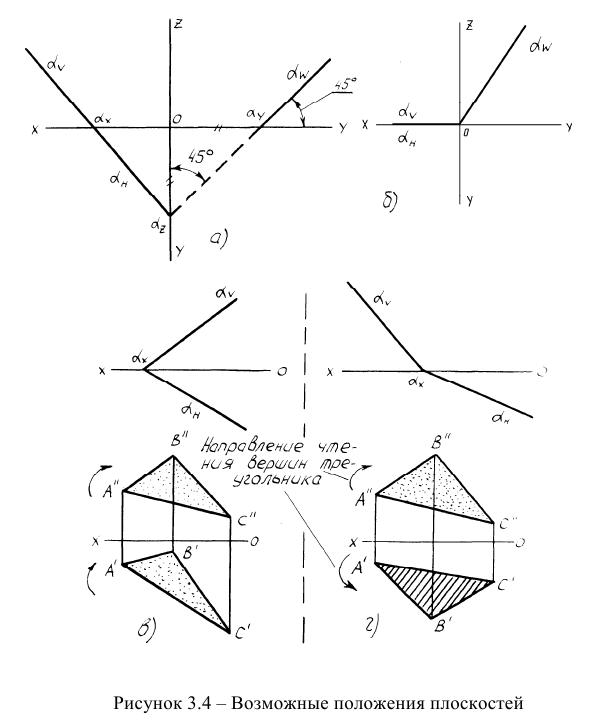
Если плоскость в пространстве равнонаклонена к какой-либо паре плоскостей проекций, то следы такой плоскости вырождаются в прямую линию (рисунок 3.4а).
Плоскости, перпендикулярные к одной из плоскостей проекций и проходящие через ось проекций, называются осевыми плоскостями. Два их следа сливаются с соответствующими осями (рисунок 3.46).
Плоскости общего положения дополнительно делятся на плоскости с односторонней (рисунок 3.4в) и двухсторонней (рисунок 3.4г) видимостью. Признаком односторонней видимости является, например, одинаковое направление чтения букв вершин треугольника на проекциях.
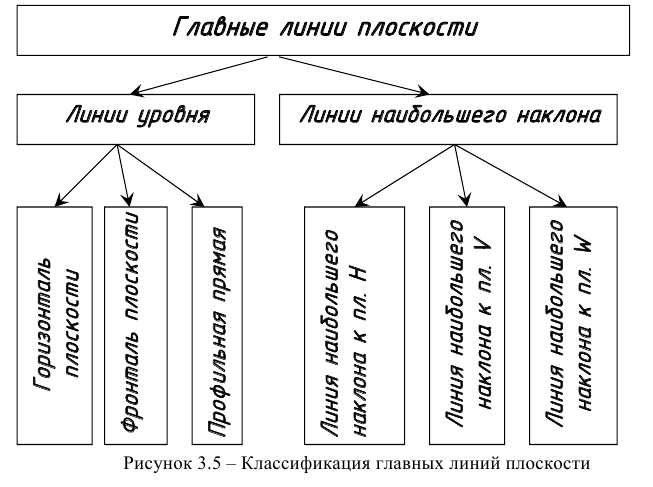
Главные линии плоскости
Главные линии плоскости делятся на линии уровня и линии наибольшего наклона. 
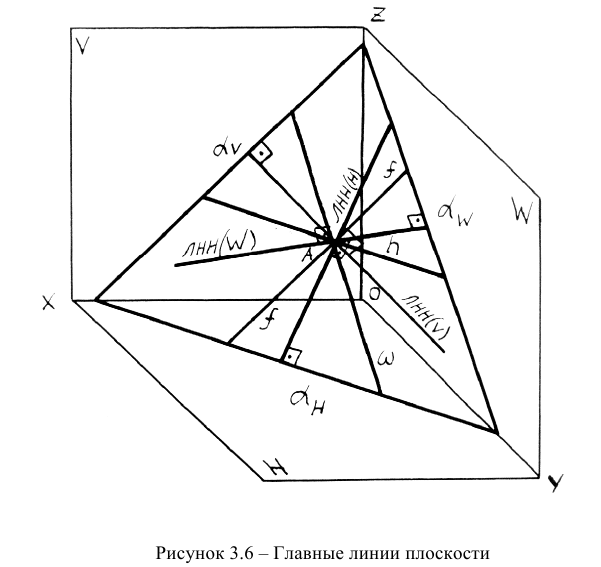
Классификация главных линий плоскости представлена на рисунке 3.5, а на рисунке 3.6 — их наглядное изображение.
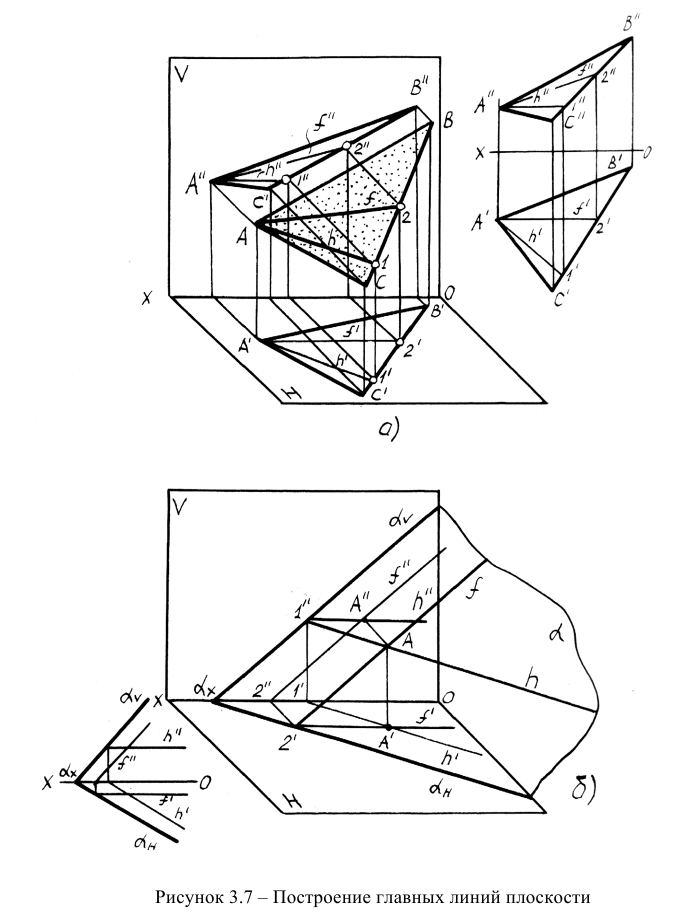
К линиям уровня относятся горизонталь, фронталь и профильная прямая плоскости. Они принадлежат плоскости и проводятся в ней по тем же правилам, что и обычные прямые. В каждой плоскости можно провести бесчисленное множество линий уровня. На рисунке 3.7 показано проведение горизонтали и фронтали в плоскостях, заданных плоской фигурой и следами.
При проведении горизонтали и фронтали в плоскости, заданной треугольником, целесообразно взять одну из вершин треугольника за точку, принадлежащую плоскости, и строить проекции h и f из этой вершины, что упрощает построения.
В плоскости, заданной следами, горизонталь проводится параллельно горизонтальному следу, а фронталь — фронтальному следу. 
В обоих случаях построение горизонтали начинают с фронтальной проекции, а построение фронтали — с горизонтальной проекции, так как они параллельны оси ОХ.
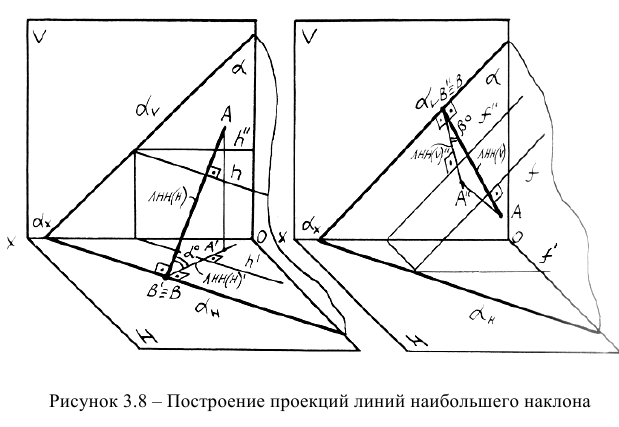
Линиями наибольшего наклона плоскости к плоскостям проекций (ЛНН) называются линии, проведенные в плоскости и определяющие наибольший угол между плоскостью и плоскостью проекций, т.е. величину образованного двугранного угла. Различают линию наибольшего наклона плоскости к плоскости проекций Н — ЛНН(Н), к плоскости проекций V -ЛНН(V) и к плоскости проекций W — ЛНН(W). Рассмотрим подробнее первые две линии.
Линия наибольшего наклона плоскости к плоскости проекций Н проводится перпендикулярно к горизонтальному следу плоскости или к горизонтали плоскости. Линия наибольшего наклона плоскости к плоскости проекций V проводится перпендикулярно к фронтальному следу плоскости или к фронтали (рисунок 3.8).
Принцип методики построения проекций ЛНН основывается на теореме прямого угла: если один из катетов прямого угла параллелен какой-либо плоскости, то на эту плоскость прямой угол проецируется в натуральную величину (см. рисунок 2.8). 
Исходя из пространственных моделей в соответствие с рисунком 3.8 и на основании теоремы о проецировании прямого угла, можно сформулировать методику построения проекций ЛНН(Н) и JIHH(V): горизонтальная проекция ЛНН(Н) проводится перпендикулярно горизонтальной проекции горизонтали или горизонтальному следу, а фронтальная проекция ЛНН(V) — перпендикулярно фронтальной проекции фронтали или фронтальному следу. Алгоритмически это может записано в следующем виде:
Проекции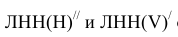 
образуются по ходу построений.
Угол наклона плоскости к плоскости проекций Н (угол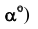 
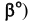
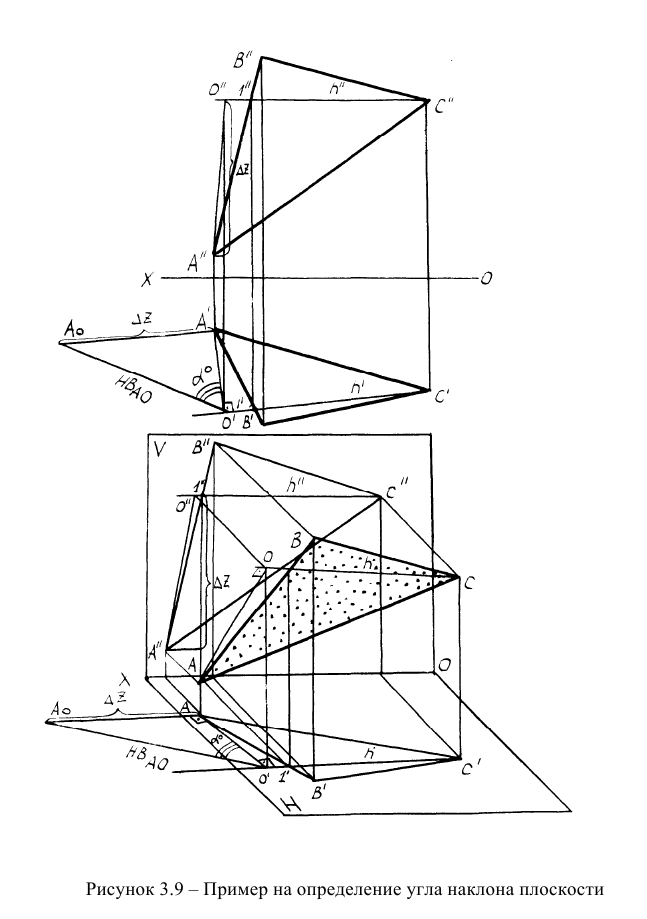
определится как угол между натуральной величиной ЛНН(Н) и её горизонтальной проекцией, а угол наклона плоскости к плоскости проекций У (угол 
— как угол между натуральной величиной ЛНН(V) и её фронтальной проекцией.
Пример: Определить угол наклона плоскости ЛВС к плоскости проекций Н (рисунок 3.9).
Решение: Для определения угла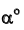 
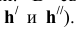
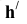
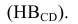
в плоскости треугольника AВС необходимо провести ЛНН(Н), которая проводится перпендикулярно горизонтали. В связи с этим проведем в плоскости горизонталь h (проекции 
Далее из точки С’ под прямым углом к 
проведем горизонтальную проекцию ЛНН 
и построим фронтальную проекцию ЛНН(Н) (C»D» ). Затем методом прямоугольного треугольника найдем натуральную величину ЛНН(Н) 
Угол а° между 
и горизонтальной проекцией линии наибольшего наклона 
— искомый. Задача на рисунке 3.9 представлена в пространственной и эпюрной формах.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Позиционные задачи
- Методы преобразования эпюра Монжа
- Касательные плоскости
- Пересечение поверхностей вращения плоскостью
- Перпендикулярность геометрических объектов
- Метод замены плоскостей проекций
- Проецирование прямой линии
- Проецирование плоскости
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник
Способы задания плоскости на эпюре
Положение плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой. Поэтому чтобы задать на эпюре плоскость, достаточно задать три ее точки (рис. 206). Плоскость можно задать точкой и прямой (рис. 207, а), двумя параллельными прямыми (рис. 207, б), двумя пересекающимися прямыми (рис. 207, в), треугольником (рис. 207, г). Можно задать плоскость следами.
 |
Следом плоскости называют прямую, по которой данная плоскость пересекает плоскость проекций. На рис. 208 Ру — фронтальный след плоскости Р, Рн — горизонтальный след плоскости Р, Pw — профильный след. плоскости Р.
Различные случаи расположения плоскостей относительно
Источник
Способы задания плоскостей эпюр плоскостей
Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:
1. тремя точками, не лежащими на одной прямой линии (рис. 41 );
 |  |  |  |
 | |||
 | |||
| а) модель | б) эпюр | ||
2. прямой линией и точкой, не принадлежащей этой прямой (рис. 4 2);
| |  |  | |
| | |||
| | |||
| а) модель | б) эпюр | ||
3. двумя пересекающимися прямыми (рис.43);
| |  |  | |
| | |||
| | |||
| а) модель | б) эпюр | ||
4. двумя параллельными прямыми (рис.44);
| |  |  | |
| | |||
| | |||
| а) модель | б) эпюр | ||
5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.45).
С ледом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная a плоскость различают горизонтальный a П1, фронтальный a П2 и профильный a П3 следы.
| |  |  | |
| | |||
| | |||
| а) модель | б) эпюр | ||
Следы плоскости общего положения пересекаются попарно на осях в точках a x , a y , a z . Эти точки называются точками схода следов , их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.
Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.
Источник
