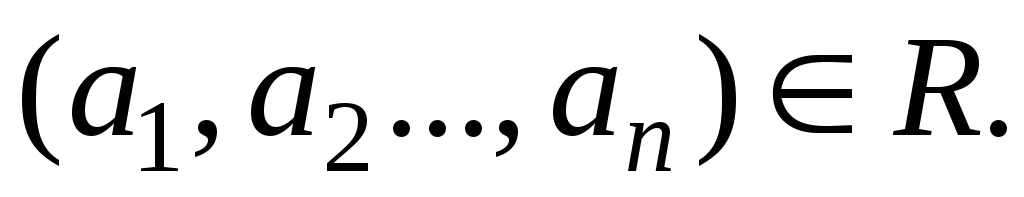6 Лекция № 5.Отношения
Продолжительность:2 часа (90 мин.)
6.1 Ключевые вопросы
6 Лекция № 5. отношения 1
6.1 Ключевые вопросы 1
6.2 Текст лекции 1
6.2.1 Отношения 1
6.2.2 Операции над отношениями 4
6.2.3 Свойства операций над отношениями 8
6.2.4 Вопросы для контроля 11
6.2 Текст лекции
6.2.1 Отношения
Отношения – один из способов задания взаимосвязей между элементами множеств. Чаще всего используются унарные и бинарные отношения.
Унарные (одноместные) отношения отражают наличие какого–то определенного признакаR (свойства и т.п.) у элементов множестваМ (например, «быть четным» на множестве натуральных чисел). Тогда все такие элементыа из множестваМ, которые отличаются данным признакомR, образуют некоторое подмножество вМ, называемое унарным отношениемR, т.е. 

Бинарные (двухместные) отношения используются для определения каких–то взаимосвязей между парами элементов множестваМ (так, на множестве людей могут быть заданы, например, следующие бинарные отношения: «жить в одном городе», «быть моложе», «быть сыном», «работать в одной организации» и т.п.). Тогда все пары (а,b) элементов изМ, между которыми имеет место данное отношениеR, образуют подмножество пар из множества всех возможных пар элементов


В общем случае могут рассматриваться п–местные (n–арные) отношения, например отношения между тройками элементов – трехместные (тернарные) отношения и т.д.
Вот пример тернарного отношения “образовывать сумму”
и отношения для четверок –“находиться в отношении пропорциональности”
Под п–местным отношением понимают подмножествоR прямого произведенияп множеств: 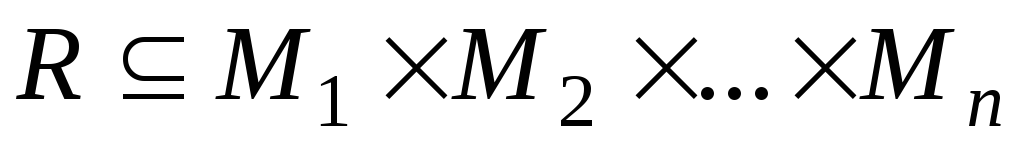
Говорят, что элементы а1, а2, . аn 
Если n–местное отношениеR задано на множествеМ, т.е.
M1= M2 =…= Mn = М, то
Рассмотрим детально бинарные отношения.
Итак, двухместным, или бинарным, отношениемR называется подмножество пар


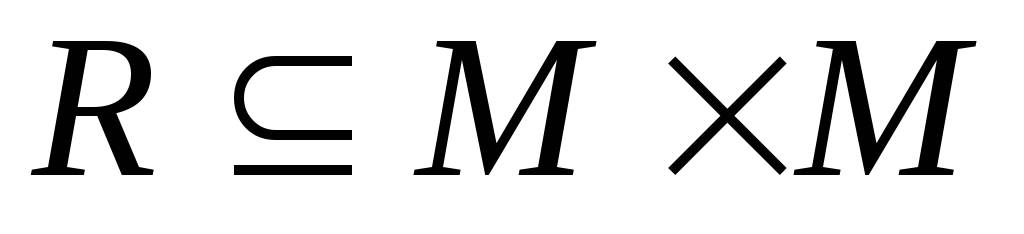
С отношениями связаны еще два понятия
– область определения D(R) и


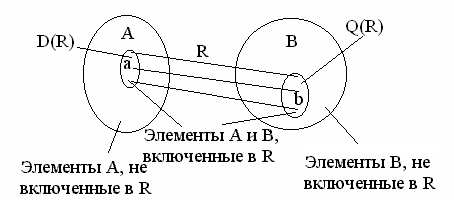
На рис. 6.1 приведен условный пример отношения
Рисунок 6.1 – Пример отношения R
Для задания бинарных отношений годятся любые способы задания множеств, так как отношения это подмножества некоторых множеств – прямых произведений двух множеств.
Отношения, определенные на конечных множествах, обычно задаются:
Кроме такого представления, заимствованного у множеств, для отношений применяют также представление в виде матриц и графов.
– Бинарному отношению 
Если 
– бинарному отношению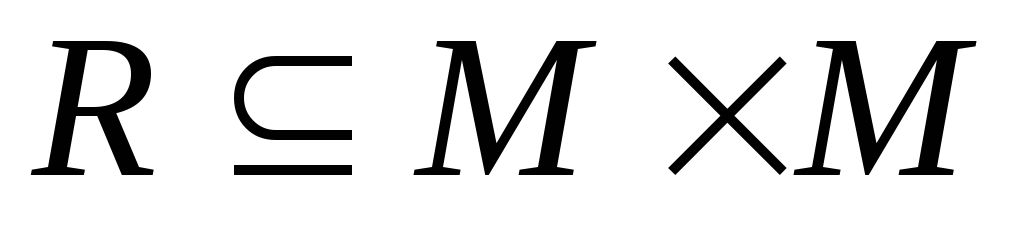
Если 
Введем следующие понятия:
Пустое отношение– отношение, которое не выполняется ни для одной пары элементов множестваМ. Обозначается это отношение символом
Матрица этого отношения содержит только 0, а граф состоит только из вершин (нуль граф).
Полное отношение– отношение, которое выполняется для любой пары элементов множестваМ. Обозначается оноU=
Матрица этого отношения содержит только 1. В графе этого отношения каждая вершина соединена дугой с каждой вершиной, включая ее самою (полный граф).
Диагональное отношениеE(оно жетождественное отношение, оно жеотношениеравенства) – отношениеaEb, которое выполняется только, еслиa и b это один и тот же элемент.
В матрице этого отношения элементы, расположенные на главной диагонали, равны 1, а остальные элементы равны 0. В графе этого отношения, кроме петель при каждой вершине, других дуг нет.
Задать в явном виде (списком), матрицей и графом отношение 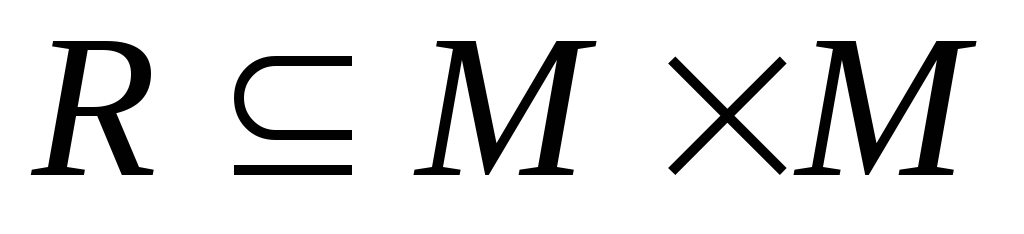
Источник
6 Лекция № 5.Отношения
Продолжительность:2 часа (90 мин.)
6.1 Ключевые вопросы
6 Лекция № 5. отношения 1
6.1 Ключевые вопросы 1
6.2 Текст лекции 1
6.2.1 Отношения 1
6.2.2 Операции над отношениями 4
6.2.3 Свойства операций над отношениями 8
6.2.4 Вопросы для контроля 11
6.2 Текст лекции
6.2.1 Отношения
Отношения – один из способов задания взаимосвязей между элементами множеств. Чаще всего используются унарные и бинарные отношения.
Унарные (одноместные) отношения отражают наличие какого–то определенного признакаR (свойства и т.п.) у элементов множестваМ (например, «быть четным» на множестве натуральных чисел). Тогда все такие элементыа из множестваМ, которые отличаются данным признакомR, образуют некоторое подмножество вМ, называемое унарным отношениемR, т.е. 

Бинарные (двухместные) отношения используются для определения каких–то взаимосвязей между парами элементов множестваМ (так, на множестве людей могут быть заданы, например, следующие бинарные отношения: «жить в одном городе», «быть моложе», «быть сыном», «работать в одной организации» и т.п.). Тогда все пары (а,b) элементов изМ, между которыми имеет место данное отношениеR, образуют подмножество пар из множества всех возможных пар элементов


В общем случае могут рассматриваться п–местные (n–арные) отношения, например отношения между тройками элементов – трехместные (тернарные) отношения и т.д.
Вот пример тернарного отношения “образовывать сумму”
и отношения для четверок –“находиться в отношении пропорциональности”
Под п–местным отношением понимают подмножествоR прямого произведенияп множеств: 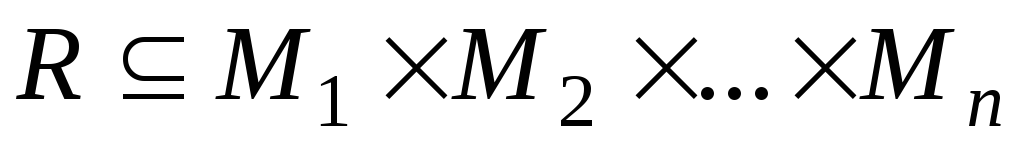
Говорят, что элементы а1, а2, . аn 
Если n–местное отношениеR задано на множествеМ, т.е.
M1= M2 =…= Mn = М, то
Рассмотрим детально бинарные отношения.
Итак, двухместным, или бинарным, отношениемR называется подмножество пар


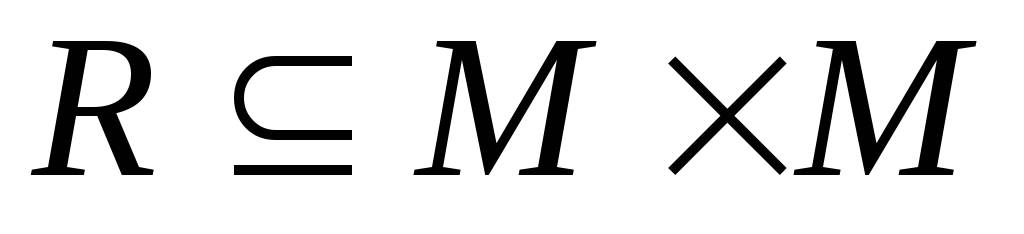
С отношениями связаны еще два понятия
– область определения D(R) и


На рис. 6.1 приведен условный пример отношения
Рисунок 6.1 – Пример отношения R
Для задания бинарных отношений годятся любые способы задания множеств, так как отношения это подмножества некоторых множеств – прямых произведений двух множеств.
Отношения, определенные на конечных множествах, обычно задаются:
Кроме такого представления, заимствованного у множеств, для отношений применяют также представление в виде матриц и графов.
– Бинарному отношению 
Если 
– бинарному отношению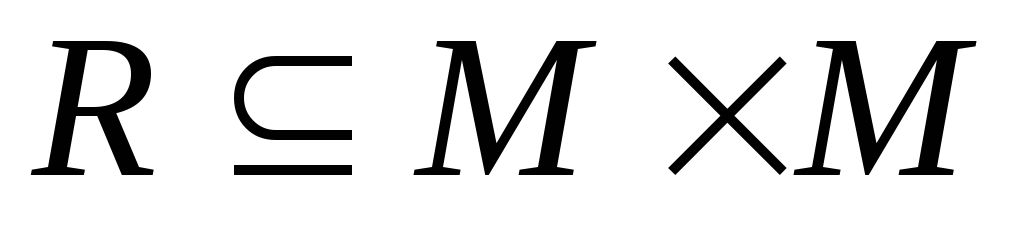
Если 
Введем следующие понятия:
Пустое отношение– отношение, которое не выполняется ни для одной пары элементов множестваМ. Обозначается это отношение символом
Матрица этого отношения содержит только 0, а граф состоит только из вершин (нуль граф).
Полное отношение– отношение, которое выполняется для любой пары элементов множестваМ. Обозначается оноU=
Матрица этого отношения содержит только 1. В графе этого отношения каждая вершина соединена дугой с каждой вершиной, включая ее самою (полный граф).
Диагональное отношениеE(оно жетождественное отношение, оно жеотношениеравенства) – отношениеaEb, которое выполняется только, еслиa и b это один и тот же элемент.
В матрице этого отношения элементы, расположенные на главной диагонали, равны 1, а остальные элементы равны 0. В графе этого отношения, кроме петель при каждой вершине, других дуг нет.
Задать в явном виде (списком), матрицей и графом отношение 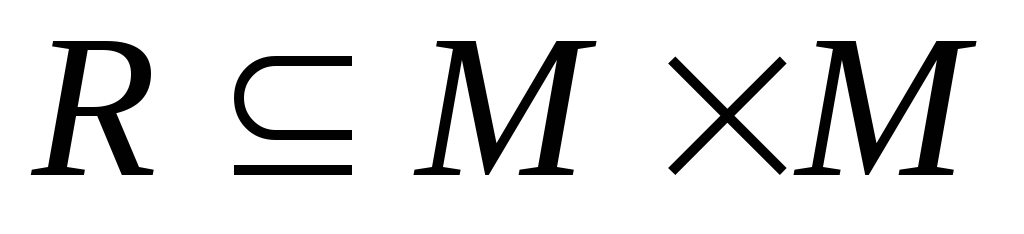
Источник