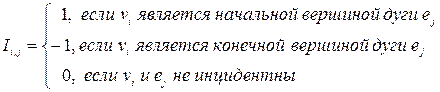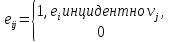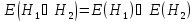Способы задания графов.
Рассмотрим три способа задания графов: графический, аналитический и матричный.
1) Графический способ.
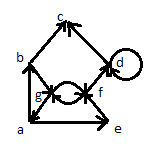
Вершины изображают точками на плоскости, а ребра – линиями, соединяющими соответствующие точки. Для изображения дуги используется линия со стрелкой, указывающей направление от начала к концу дуги.
На рисунке 12 изображен смешанный граф с вершинами v1, v2,¼, v6, ребрами e1, e2, e3, e5 и дугой e4. Смежные вершины v1, v2, инциденты ребру e1. Вершины v1, v3, инциденты параллельным ребрам e2 и e3. Вершине v4 инциденты петля e5 и дуга e4, причем v4 является началом дуги e4, а v5 – концом этой дуги. Степень вершины v1 равна 3, вершины v2 – 1, вершины v3 – 2, вершины v4 – 3, вершины v5 – 1, вершины v6 – 0. Таким образом, вершины v2 и v5 – висячие, а вершина v6 – изолированная. В случае дуги e4 точнее было бы говорить о полустепенях исхода и захода вершин v4 и v5, а именно: полустепень исхода вершины v4 равна 3, вершины v5 – 0, полустепень захода вершины v4 равна 2, вершины v5 – 1.
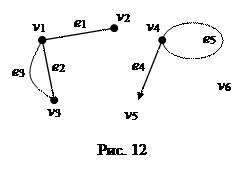
2) Аналитический способ.
3) Матричный способ.
Имеется несколько вариантов задать граф матрицей. Наиболее употребимыми являются матрица инциденций и матрица смежности.
а) Матрица инциденций – это прямоугольная матрица, число строк которой равно числу вершин, а число столбцов – числу дуг (ребер) графа. Элементы этой матрицы определяются следующим образом:
Таким образом, для графа на рисунке 12 матрица инциденций такова:
| e1 | e2 | e3 | e4 | e5 |
| v1 | ||||
| v2 | ||||
| I= | v3 | |||
| v4 | ||||
| v5 | -1 | |||
| v6 |
По этой матрице легко судить о наличии в графе параллельных ребер (два одинаковых столбца), петли (одна единица в столбце), дуги (значения разных знаков в столбце), изолированной вершины (нулевая строка), висячих вершин (одно ненулевое значение в строке).
б) Матрица смежности вершин – это квадратная матрица, размер которой определяется числом вершин в графе. Элементы этой матрицы определяются так: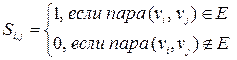 
. Если в графе имеются параллельные ребра, то соответствующий элемент матрицы смежности полагают равным числу этих ребер. Так матрица смежности для графа на рисунке 12 такова:
| v1 | v2 | v3 | v4 | v5 | v6 |
| v1 | |||||
| v2 | |||||
| S= | v3 | ||||
| v4 | |||||
| v5 | |||||
| v6 |
По виду этой матрицы также несложно судить о наличии в графе кратных ребер, дуг, петель, висячих и изолированных вершин.
Дата добавления: 2015-10-19 ; просмотров: 17443 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
MT1100: Дискретная математика
Помимо геометрического (графического) и аналитического способов задания графов существует еще, как минимум, три эквивалентых им способа.
Матрицей смежности для графа %%G = (V, E)%% называется квадратная матрица %%A = (a_
$$ A = \begin
Матрица смежности для примера из «Основных понятий»
Списком ребер графа называется таблица, состоящая из двух столбцов, в которой на пересечении %%i%%-й строки и первого (левого) столбца записывается ребро %%e_i%%, а на пересечении %%i%% -й строки и второго (правого) столбца записываются вершины, инцидентные ребру %%e_i%%.
Для того, чтобы список ребер однозначно задавал граф, необходимо помимо списка ребер указать множество всех изолированных вершин этого графа.
| 1 | %%B, C%% |
| 2 | %%A, C%% |
| 3 | %%B, F%% |
| 4 | %%A, F%% |
| 5 | %%A, F%% |
| 6 | %%A, D%% |
| 7 | %%D, F%% |
| 8 | %%D, E%% |
| 9 | %%E, F%% |
| 10 | %%B, E%% |
| 11 | %%E, E%% |
Список ребер для примера из «Основных понятий»
Матрицей инцидентности для графа %%G = (V, E)%% называется матрица %%B = (b_
Для неориентированного графа %%b_
У матрицы инцидентности есть пара особенностей:
- в каждой строке должны стоять две единицы, а все остальные символы — нули;
- она не используется для графов с петлями.
$$ B = \begin
Матрица инцидентности для примера из «Основных понятий» с учетом удаления петли у %%E%%
Источник
41.Способы задания графов.
Способы задания графов:
Задание графа при помощи матрицы инцидентности
n
m – где n кол-во вершин графа, m – кол-во ребер графа. По вертикали и горизонтали указываются вершины и ребра, а на пересечении i-строки и j-столбца, если ребро i инцидентно вершине j ставим 1 и 0 в противном случае.
В случае орграфа
В петле присваивается любое другое число. (чаще всего 2)
Списком ребер графа
Список ребер графа представл. столбцом. В левом столбце перечисляется все ребра, а в правом инцидентные ему вершины, причем для n-графа порядок написания вершин произвольный, а для ор-графа первым стоит номер начала дуги.
Если граф имеет изолированные вершины, то они помещаются в конец списка.
Матрица смежности — это квадратная матрица 
размера
, гдеn – кол-во вершин графа.
В случае n-графа проставляется число ребер соединяющих эти две вершины.
В случае ор-графа проставляется кол-во дуг имеющих начало в вершине 
и конец в вершине
.
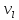
Определение 2.21. Матрицей смежности конечного графа G с p вершинами называется матрица A(G)=||aij|| (i, j = 1, 2, …, p), в которой если смежны вершины то ставим 1, иначе 0.
42. Действия над графами.
Граф H будем называть частью графа G(
), если мн-воV(H) и мн-во ребер E(H) содержится в соответствующих мн-вах для графа G: 
и
.
Граф H называется суграфом графа G, если он является частью графа G и кол-во вершин графа H равно кол-ву вершин графа G, т.е.V(H)=V(G).
Граф G(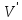
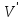
) назыв.подграфом графа G(V), если граф G(
) содержит все ребра, которые инцидентны вершинам из мн-ва
.
Определим некоторые операции на графах:
Удаление или добавление ребра.
Удаление вершины. Из множества вершин удаляем выбранную вершину, а из множества ребер все инцидентные ей ребра.
Стягивание ребра. Отождествляем (стягиваем) вершины инцидентные выбранному ребру.
Добавление вершины (разбиение ребра). Выберем некоторое ребро (u,v) из множества ребер и удалим его. В множество вершин добавим новую вершину w, а в множество ребер новые ребра (u,w) и (w,v).
Дополнение 
части H графа G явл. графом удовлетворяющим след. условиям:
1)
=
2)
Сумма 
и
Произведение 
: 
и
43. Ориентированные и неориентированные графы.
Графом G называется совокупность 2-х множеств (V, E), где V – множество вершин графа, а Е – множество ребер графа. Между вершинами и ребрами графа G устанавливают отношение инцидентности. Считают, что ребро 
инцидентно вершинам 
,
, если оно соединяет эти 2-е вершины. При этом вершины
,
называютсясмежными. Отношение инцидентности является самым главным элементом графа, т.к. указывает способ объединения множеств V и E в единый объект. Если ребро 
, соединяющее 2-е вершины, направлено от одной вершины к другой, то оно называетсяориентированным или дугой и графически изображается стрелками, направленными от начала к концу. Граф, содержащий дуги называется ориентированным или орграфом. Граф, не содержащий ни одной дуги (содержащий только ребра) называется неориентированным или н-графом.
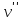
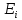
Н-ГРАФ (Рис.1) ОР-ГРАФ(Рис.2)
Ребра, инцидентные одной и той же паре вершин называются кратными (на рис.1 это ребра 8 и 9).
Источник
Способы задания неориентированного графа
3.1 пТЙЕОФЙТПЧБООЩЕ Й ОЕПТЙЕОФЙТПЧБООЩЕ ЗТБЖЩ.
уРПУПВЩ ЪБДБОЙС ЗТБЖПЧ
1. зТБЖ — ЬФП УЙУФЕНБ ОЕЛПФПТЩИ ПВЯЕЛФПЧ ЧНЕУФЕ У ОЕЛПФПТЩНЙ РБТБНЙ ЬФЙИ ПВЯЕЛФПЧ, ЙЪПВТБЦБАЭБС ПФОПЫЕОЙС УЧСЪЙ НЕЦДХ ОЙНЙ. зТБЖБНЙ ХДПВОП ЙЪПВТБЦБАФУС УЕФЙ ЛПННХОЙЛБГЙК, ДЙУЛТЕФОЩЕ НОПЗПЫБЗПЧЩЕ РТПГЕУУЩ, УЙУФЕНЩ ВЙОБТОЩИ ПФОПЫЕОЙК, ИЙНЙЮЕУЛЙЕ УФТХЛФХТОЩЕ ЖПТНХМЩ, ТБЪМЙЮОЩЕ УИЕНЩ Й ДЙБЗТБННЩ Й ДТ.
оЕПТЙЕОФЙТПЧБООЩК ЗТБЖ (УППФЧЕФУФЧЕООП ПТЙЕОФЙТПЧБООЩК ЗТБЖ, ЙМЙ ПТЗТБЖ) G — УЙУФЕНБ G = (V, е, з), УПУФПСЭБС ЙЪ НОПЦЕУФЧБ ЬМЕНЕОФПЧ V = 
V 2 , УФБЧСЭЕЗП Ч УППФЧЕФУФЧЙЕ ЛБЦДПНХ ЬМЕНЕОФХ Е ™ е ОЕХРПТСДПЮЕООХА (УППФЧЕФУФЧЕООП ХРПТСДПЮЕООХА) РБТХ ЬМЕНЕОФПЧ v1, v2 ™ V, ОБЪЩЧБЕНЩИ ЛПОГБНЙ ТЕВТБ Е.
V U E ПВТБЪХЕФ НОПЦЕУФЧП ЬМЕНЕОФПЧ ЗТБЖБ; РТЙ ЬФПН РТЕДРПМБЗБЕФУС, ЮФП е 
V= Ø. пФПВТБЦЕОЙЕ з ПРТЕДЕМСЕФ ПФОПЫЕОЙЕ ЙОГЙДЕОФОПУФЙ ТЕВТБ У ЛБЦДЩН ЙЪ УЧПЙИ ЛПОГПЧ. дМС ЗТБЖБ G = (V, е, з) ХРПФТЕВМСЕФУС ФБЛЦЕ ВПМЕЕ ЛПТПФЛПЕ ПВПЪОБЮЕОЙЕ G = (V, е) ВЕЪ ХЛБЪБОЙС ЙОГЙДЕОФОПУФЕК, ЛПФПТЩЕ ПРТЕДЕМСАФУС ЛПОФЕЛУФПН. рП ЛПМЙЮЕУФЧХ ЬМЕНЕОФПЧ ЗТБЖЩ ДЕМСФУС ОБ ЛПОЕЮОЩЕ Й ВЕУЛПОЕЮОЩЕ. ъДЕУШ НЩ ВХДЕН ТБУУНБФТЙЧБФШ, Ч ПУОПЧОПН, ЛПОЕЮОЩЕ ЗТБЖЩ, ОЕ ПЗПЧБТЙЧБС ЬФПЗП УРЕГЙБМШОП.
еУМЙ з(Е) = (v1, v2) — ХРПТСДПЮЕООБС РБТБ (Ф.Е. (v1, v2) 
(v2, v1) РТЙ v1 v2), ФП ТЕВТП Е ОБЪЩЧБЕФУС ПТЙЕОФЙТПЧБООПК ДХЗПК, ЙУИПДСЭЕК ЙЪ ЧЕТЫЙОЩ v, Й ЧИПДСЭЕК Ч ЧЕТЫЙОХ v2; v1 ОБЪЩЧБЕФУС ОБЮБМПН, a v2 — ЛПОГПН ДХЗЙ Е. еУМЙ з(Е) = (v1, v2) — ОЕХРПТСДПЮЕООБС РБТБ, ФП ТЕВТП Е ОБЪЩЧБЕФУС ОЕПТЙЕОФЙТПЧБООЩН. чУСЛПНХ ЗТБЖХ G НПЦОП РПУФБЧЙФШ Ч УППФЧЕФУФЧЙЕ УППФОЕУЕООЩК ОЕПТЙЕОФЙТПЧБООЩК ЗТБЖ 
У ФЕНЙ ЦЕ НОПЦЕУФЧБНЙ V Й е Й ЙОГЙДЕОФОПУФСНЙ, ОП ЧУЕ РБТЩ ОЕХРПТСДПЮЕООЩЕ.
чЕТЫЙОБ, ОЕ ЙОГЙДЕОФОБС ОЙ ПДОПНХ ТЕВТХ, ОБЪЩЧБЕФУС ЙЪПМЙТПЧБООПК. чЕТЫЙОБ, ЙОГЙДЕОФОБС ТПЧОП ПДОПНХ ТЕВТХ, Й УБНП ЬФП ТЕВТП ОБЪЩЧБАФУС ЛПОГЕЧЩНЙ, ЙМЙ ЧЙУСЮЙНЙ. тЕВТП У УПЧРБДБАЭЙНЙ ЛПОГБНЙ ОБЪЩЧБЕФУС РЕФМЕК. дЧЕ ЧЕТЫЙОЩ, ЙОГЙДЕОФОЩЕ ПДОПНХ Й ФПНХ ЦЕ ТЕВТХ, ОБЪЩЧБАФУС УПУЕДОЙНЙ (ЙМЙ УНЕЦОЩНЙ). дЧБ ТЕВТБ, ЙОГЙДЕОФОЩЕ ПДОПК Й ФПК ЦЕ ЧЕТЫЙОЕ, ОБЪЩЧБАФУС УНЕЦОЩНЙ. тЕВТБ, ЛПФПТЩН РПУФБЧМЕОБ Ч УППФЧЕФУФЧЙЕ ПДОБ Й ФБ ЦЕ РБТБ ЧЕТЫЙО, ОБЪЩЧБАФУС ЛТБФОЩНЙ, ЙМЙ РБТБММЕМШОЩНЙ. дМС ТБЪМЙЮОЩИ ЪБДБЮ ПДОПНХ Й ФПНХ ЦЕ ПВЯЕЛФХ НПЦОП УПРПУФБЧЙФШ; ЗТБЖ РП-ТБЪОПНХ. фБЛ, ЖТБЗНЕОФ ДПТПЦОПК УЕФЙ НПЦЕФ ВЩФШ, РТЕДУФБЧМЕО ОЕПТЙЕОФЙТПЧБООЩН ТЕВТПН, ЙЪПВТБЦБАЭЙН ОБМЙЮЙЕ УЧСЪЙ НЕЦДХ ЕЗП ЛПОГБНЙ (ОБУЕМЕООЩНЙ РХОЛФБНЙ, ЗПТПДУЛЙНЙ РМПЭБДСНЙ ЙМЙ РЕТЕЛТЕУФЛБНЙ); ПДОПК ЙМЙ ДЧХНС ДХЗБНЙ, РЕТЕДБАЭЙНЙ ПДОПУФПТПООЕЕ ЙМЙ ДЧХУФПТПООЕЕ ДЧЙЦЕОЙЕ ФТБОУРПТФБ; ОЕУЛПМШЛЙНЙ ДХЗБНЙ — ПФДЕМШОП ДМС ЛБЦДПЗП ТСДБ ДЧЙЦЕОЙС. тЕВТБН НПЗХФ ВЩФШ, РТЙРЙУБОЩ ФБЛЦЕ ЮЙУМБ, ПЪОБЮБАЭЙЕ ДМЙОХ, ТСДОПУФШ, ХЛМПО Й ДТХЗЙЕ ЮЙУМЕООЩЕ ЙМЙ ЙОЩЕ ИБТБЛФЕТЙУФЙЛЙ.
2. юБУФП ВЩЧБЕФ ЧБЦОП ПРТЕДЕМЙФШ, ЛБЛЙЕ ЗТБЖЩ УЮЙФБАФУС ТБЪМЙЮОЩНЙ, Б ЛБЛЙЕ ОЕ ТБЪМЙЮБАФУС. пВЩЮОП ЬФП УЧСЪЩЧБАФ У РПОСФЙЕН ЙЪПНПТЖЙЪНБ ЗТБЖПЧ. дЧБ ЗТБЖБ G1= (V1, E1, з1) Й G2= (V2, е2, з2) ОБЪЩЧБАФУС ЙЪПНПТЖОЩНЙ, ЕУМЙ УХЭЕУФЧХАФ ЧЪБЙНОП ПДОПЪОБЮОЩЕ ПФПВТБЦЕОЙС f: V1 V2 Й g: е1 е2, УПИТБОСАЭЙЕ ЙОГЙДЕОФОПУФШ, Ф.Е. ФБЛЙЕ, ЮФП ДМС ЧУСЛПЗП Е ™ е, ТБЧЕОУФЧП з1(e) = (v1,v2) ЧМЕЮЕФ ЪБ УПВПК ТБЧЕОУФЧП з2 (gЕ) = (fv1, fv2).
чП НОПЗЙИ УМХЮБСИ НПЦОП ТБУУНБФТЙЧБФШ ЗТБЖЩ У ФПЮОПУФША ДП ЙЪПНПТЖЙЪНБ, Ф.Е. ОЕ ТБЪМЙЮБФШ ЙЪПНПТЖОЩЕ ЗТБЖЩ; ПДОБЛП, ЕУМЙ ЛБЛЙЕ-ФП ЧЕТЫЙОЩ ЙМЙ ТЕВТБ ЗТБЖПЧ ПВМБДБАФ ТБЪМЙЮОПК ЙОДЙЧЙДХБМШОПУФША, ОБРТЙНЕТ, ПОЙ ЪБОХНЕТПЧБОЩ ЙМЙ ЙН УПРПУФБЧМЕОЩ ЛБЛЙЕ-МЙВП ЮЙУМЕООЩЕ ИБТБЛФЕТЙУФЙЛЙ (ЧЕУ ТЕВТБ, ДМЙОБ ТЕВТБ Й ДТ.), ФП ЕУФЕУФЧЕООП РТЙ УТБЧОЕОЙЙ ДЧХИ ЗТБЖПЧ ЬФХ ЙОДЙЧЙДХБМШОПУФШ ХЮЙФЩЧБФШ.
3. уХЭЕУФЧХЕФ ОЕУЛПМШЛП УРПУПВПЧ ЪБДБОЙС ЗТБЖПЧ, УЧСЪБООЩИ У ТБЪМЙЮОПК ЖПТНПК ЪБДБОЙС ЖХОЛГЙЙ з. чПФ ОЕЛПФПТЩЕ ЙЪ ОЙИ ДМС ЛПОЕЮОЩИ
1) рЕТЕЮЙУМЕОЙЕ (УРЙУПЛ) ТЕВЕТ ЗТБЖБ У ХЛБЪБОЙЕН ЙИ ЛПОГПЧ Й ДПВБЧМЕОЙЕН УРЙУЛБ ЙЪПМЙТПЧБООЩИ ЧЕТЫЙО.
2) нБФТЙГБ ЙОГЙДЕОГЙК ЗТБЖБ У b ЧЕТЫЙОБНЙ Й Т ТЕВТБНЙ — РТСНПХЗПМШОБС НБФТЙГБ б = ||Бij|| У b УФТПЛБНЙ Й Т УФПМВГБНЙ, УФТПЛХ ЛПФПТПК УППФЧЕФУФЧХАФ ЧЕТЫЙОБН ЗТБЖБ, Б УФПМВГЩ — ТЕВТБН, РТЙЮЕН ДМС ОЕПТЙЕОФЙТПЧБООПЗП ЗТБЖБ ЬМЕНЕОФ НБФТЙГЩ aij ТБЧЕО 1, ЕУМЙ ЧЕТЫЙОБ Vi Й ТЕВТП Еj ЙОГЙДЕОФОЩ, Й ТБЧЕО 0 Ч РТПФЙЧОПН УМХЮБЕ. дМС ПТЙЕОФЙТПЧБООПЗП ЗТБЖБ Бij = -1, ЕУМЙ Vi СЧМСЕФУС ОБЮБМПН ДХЗЙ Еj, Й Бij +1, ЕУМЙ V1 — ЛПОЕГ ДХЗЙ Еj. ч ЛБЦДПН УФПМВГЕ НБФТЙГЩ ЙОГЙДЕОГЙК — ДЧБ ОЕОХМЕЧЩИ ЬМЕНЕОФБ, ЕУМЙ ТЕВТП — ОЕ РЕФМС. рЕФМЕ УППФЧЕФУФЧХЕФ ЬМЕНЕОФ, ТБЧОЩК 2.
3) нБФТЙГБ УПУЕДУФЧБ (УНЕЦОПУФЙ) ЧЕТЫЙО ЗТБЖБ У b ЧЕТЫЙОБНЙ — ЛЧБДТБФОБС НБФТЙГБ ч =||bij|| ТБЪНЕТОПУФЙ b, УФТПЛЙ Й УФПМВГЩ ЛПФПТПК УППФЧЕФУФЧХАФ ЧЕТЫЙОБН ЗТБЖБ, РТЙЮЕН ОЕПФТЙГБФЕМШОЩК ЬМЕНЕОФ b ТБЧЕО ЮЙУМХ ТЕВЕТ, ЙДХЭЙИ ЙЪ ЧЕТЫЙОЩ vi Ч ЧЕТЫЙОХ Vj (bij ОЕ ТБЧОП, ЧППВЭЕ ЗПЧПТС, шji, ПДОБЛП ДМС ОЕПТЙЕОФЙТПЧБООЩИ ЗТБЖПЧ НБФТЙГБ УПУЕДУФЧБ — УЙННЕФТЙЮОБС). дМС ОЕУНЕЦОЩИ ЧЕТЫЙО УППФЧЕФУФЧХАЭЙК ЬМЕНЕОФ НБФТЙГЩ ТБЧЕО 0.
еУМЙ НБФТЙГБ ЙОГЙДЕОГЙК ЪБДБЕФ ЗТБЖ ПДОПЪОБЮОП, ФП НБФТЙГБ УПУЕДУФЧБ ЧЕТЫЙО ПРТЕДЕМСЕФ ЗТБЖ У ФПЮОПУФША ДП ЪБНЕОЩ МАВПЗП ОЕПТЙЕОФЙТПЧБООПЗП ТЕВТБ РБТПК РТПФЙЧПРПМПЦОП ОБРТБЧМЕООЩИ ДХЗ НЕЦДХ ФЕНЙ ЦЕ ЧЕТЫЙОБНЙ. пДОБЛП ДМС ЗТБЖПЧ ВЕЪ ЛТБФОЩИ ТЕВЕТ ЪБДБОЙЕ ЗТБЖБ Й ЬФПК НБФТЙГЕК ПДОПЪОБЮОП, ЬМЕНЕОФЩ НБФТЙГЩ УПУЕДУФЧБ ТБЧОЩ Ч ЬФПН УМХЮБЕ 0 ЙМЙ 1.
4) дМС ОБЗМСДОПУФЙ ЗТБЖ ЮБУФП РТЕДУФБЧМСАФ Ч ЧЙДЕ ЗЕПНЕФТЙЮЕУЛПЗП ПВЯЕЛФБ: ЧЕТЫЙОБН УППФЧЕФУФЧХАФ ТБЪМЙЮОЩЕ ЧЩДЕМЕООЩЕ ФПЮЛЙ Ч РТПУФТБОУФЧЕ (ОБ РМПУЛПУФЙ), ТЕВТБН — ПФТЕЪЛЙ ЛТЙЧЩИ, УЧСЪЩЧБАЭЙЕ УППФЧЕФУФЧХАЭЙЕ ФПЮЛЙ Й ОЕ РТПИПДСЭЙЕ ЮЕТЕЪ ЧЩДЕМЕООЩЕ ФПЮЛЙ, ПФМЙЮОЩЕ ПФ ЙИ ЛПОГПЧ. пФОПЫЕОЙА ЙОГЙДЕОФОПУФЙ ЧЕТЫЙО Й ТЕВЕТ ЗТБЖБ УППФЧЕФУФЧХЕФ РТЙ ЬФПН ЗЕПНЕФТЙЮЕУЛБС ЙОГЙДЕОФОПУФШ ЧЩДЕМЕООЩИ ФПЮЕЛ Й МЙОЙК. лТПНЕ ФПЗП, РТЕДРПМБЗБЕФУС, ЮФП ЛТЙЧЩЕ РПРБТОП ОЕ РЕТЕУЕЛБАФУС ЧП ЧОХФТЕООЙИ ФПЮЛБИ. фБЛПЕ РТЕДУФБЧМЕОЙЕ ЗТБЖБ ОБЪЩЧБЕФУС ТЕБМЙЪБГЙЕК.
нПЦОП РПЛБЪБФШ, ЮФП ЧУСЛЙК ЗТБЖ У ЛПОЕЮОЩН (Й ДБЦЕ УЮЕФОЩН) ЮЙУМПН ЬМЕНЕОФПЧ НПЦЕФ ВЩФШ ТЕБМЙЪПЧБО Ч ФТЕИНЕТОПН РТПУФТБОУФЧЕ, РТЙЮЕН, ЕУМЙ ЗТБЖ ОЕ УПДЕТЦЙФ ЛТБФОЩИ ТЕВЕТ, ФП ТЕВТБ НПЦОП ТЕБМЙЪПЧБФШ РТСНПМЙОЕКОЩНЙ ПФТЕЪЛБНЙ. оБ РМПУЛПУФЙ ТЕБМЙЪХЕФУС ОЕ ЧУСЛЙК ЗТБЖ, ЮФП РПТПЦДБЕФ ТБЪДЕМЕОЙЕ ЗТБЖПЧ ОБ РМПУЛЙЕ Й ОЕРМПУЛЙЕ. фЕН ОЕ НЕОЕЕ ДБЦЕ ОЕРМПУЛЙК ЗТБЖ ВЩЧБЕФ ХДПВОП ЙЪПВТБЦБФШ ОБ РМПУЛПУФЙ, ОБДП ФПМШЛП ПФМЙЮБФШ ЧЕТЫЙОЩ ПФ РЕТЕУЕЮЕОЙК ТЕВЕТ ОБ ТЙУХОЛЕ (ОБРТЙНЕТ, ЙЪПВТБЦБФШ ЧЕТЫЙОЩ ЛТХЦЛБНЙ); ПТЙЕОФБГЙА ТЕВЕТ РПЛБЪЩЧБАФ УФТЕМЛБНЙ.
еУМЙ РТЕДУФБЧЙФШ ЗТБЖПН ХМЙЮОХА (ДПТПЦОХА) УЕФШ, ЗДЕ ТЕВТБ ЙЪПВТБЦБАФ ПФТЕЪЛЙ ДПТПЗ, УЧСЪЩЧБАЭЙЕ УПУЕДОЙЕ ЧЕТЫЙОЩ (РМПЭБДЙ Й РЕТЕЛТЕУФЛЙ), ФП ДМС ОЕВПМШЫПЗП ОБУЕМЕООПЗП РХОЛФБ ФБЛПК ЗТБЖ НПЦЕФ ВЩФШ РМПУЛЙН, ОП ДМС ЗПТПДБ У РХФЕРТПЧПДБНЙ, НПУФБНЙ Й ФТБОУРПТФОЩНЙ ТБЪЧСЪЛБНЙ Ч ТБЪОЩИ ХТПЧОСИ, ПО УЛПТЕЕ ЧУЕЗП ОЕРМПУЛЙК. 
оБ ТЙУХОЛЕ 1 ЙЪПВТБЦЕО ЗТБЖ У 8 ЧЕТЫЙОБНЙ Й 11 ТЕВТБНЙ Й РТПЙММАУФТЙТПЧБОЩ ОЕЛПФПТЩЕ ЧЧЕДЕООЩЕ РПОСФЙС: ТЕВТБ Е1,Е3,Е6, e7, e9, e10 СЧМСАФУС ДХЗБНЙ; v6 — ЙЪПМЙТПЧБООБС ЧЕТЫЙОБ; Е4 Й Е5 -РБТБММЕМШОЩЕ ТЕВТБ; Е6 Е7, Е8, Е9 — ФБЛЦЕ РБТБММЕМШОЩЕ ТЕВТБ, Е11 -РЕФМС; v2 Й v3, v2 Й v4 — РБТЩ УПУЕДОЙИ ЧЕТЫЙО; Е3 Й Е4 — РБТБ УНЕЦОЩИ ТЕВЕТ. нБФТЙГБ ЙОГЙДЕОГЙК б Й НБФТЙГБ УПУЕДУФЧБ ЧЕТЫЙО ч ЬФПЗП ЗТБЖБ ФБЛПЧЩ:
| A= |  | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |  |
| -1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | -1 | 1 | 1 | -1 | -1 | 1 | 1 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | -1 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 |
| B= | | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 1 | 0 | 2 | 0 | 0 | 0 | 0 | |||
| 0 | 1 | 2 | 0 | 3 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
4. тБУУНПФТЙН ОЕУЛПМШЛП РТЙНЕТПЧ ЗТБЖПЧ, ЙНЕАЭЙИ ЙОФЕТЕУОЩЕ РТЙНЕОЕОЙС.
(1)рПМОЩН ЗТБЖПН ОБЪЩЧБЕФУС ЗТБЖ ВЕЪ ЛТБФОЩИ ТЕВЕТ (Й ЙОПЗДБ ВЕЪ РЕФЕМШ), Ч ЛПФПТПН МАВЩЕ ДЧЕ ЧЕТЫЙОЩ УПЕДЙОЕОЩ ТЕВТПН (ПТЙЕОФЙТПЧБООЩН ЙМЙ ОЕПТЙЕОФЙТПЧБООЩН). рПМОЩК ОЕПТЙЕОФЙТПЧБООЩК ЗТБЖ У b ЧЕТЫЙОБНЙ ПВПЪОБЮБЕФУС лb. пЮЕЧЙДОП, ЗТБЖ лb УПДЕТЦЙФ уb 2 = b * (b — 1) / 2 ТЕВЕТ. рПМОЩК ПТЙЕОФЙТПЧБООЩК ЗТБЖ ЙОПЗДБ ОБЪЩЧБАФ ФХТОЙТПН, РПУЛПМШЛХ ПО ПФТБЦБЕФ ТЕЪХМШФБФ УПУФСЪБОЙС РП ЛТХЗПЧПК УЙУФЕНЕ Ч ПДЙО ЛТХЗ. рПМОЩК ЗТБЖ РТЕДУФБЧМСЕФ ВЙОБТОПЕ ПФОПЫЕОЙЕ R: ЕУМЙ R ТЕЖМЕЛУЙЧОП, ФП ЗТБЖ — У РЕФМСНЙ; ЕУМЙ R УЙННЕФТЙЮОП, ФП ЗТБЖ — ОЕПТЙЕОФЙТПЧБООЩК, ЕУМЙ R БОФЙУЙННЕФТЙЮОП, ФП — ПТЙЕОФЙТПЧБООЩК.
оБ ТЙУХОЛЕ 2 Б, В, Ч ЙЪПВТБЦЕОЩ ЗТБЖЩ л3, л4, л5. оБ ТЙУХОЛЕ 2 З ЗТБЖ л5 РТЕДУФБЧМЕО У НЙОЙНБМШОЩН ЮЙУМПН РЕТЕУЕЮЕОЙК ЙЪПВТБЦЕОЙК ТЕВЕТ: ХУФТБОЙФШ ЙИ РПМОПУФША ОЕМШЪС.
 |  |  |  |
| a | В | Ч | З |
| тЙУХОПЛ 2 | |||
(2) дЧХДПМШОЩН ЗТБЖПН ОБЪЩЧБЕФУС ЗТБЖ, ЧЕТЫЙОЩ ЛПФПТПЗП ТБЪВЙФЩ ОБ ДЧБ ОЕРЕТЕУЕЛБАЭЙИУС ЛМБУУБ: V = V1, U V2, Б ТЕВТБ УЧСЪЩЧБАФ ЧЕТЫЙОЩ ФПМШЛП ЙЪ ТБЪОЩИ ЛМБУУПЧ — ОЕ ПВСЪБФЕМШОП ЧУЕ РБТЩ (ТЙУХОПЛ 3). еУМЙ ЦЕ ЛБЦДБС ЙЪ ЧЕТЫЙО ЛМБУУБ V, УЧСЪБОБ ТЕВТПН У ЛБЦДПК ЧЕТЫЙОПК ЛМБУУБ V2, ФП ЗТБЖ ОБЪЩЧБЕФУС РПМОЩН ДЧХДПМШОЩН Й ПВПЪОБЮБЕФУС Km,n, ЗДЕ m = |V1, |, n = | V2|. пЮЕЧЙДОП, ЗТБЖ Km,n УПДЕТЦЙФ (m+n) ЧЕТЫЙО Й m • n ТЕВЕТ. оБ ТЙУХОЛЕ ъ Б ЙЪПВТБЦЕО ДЧХДПМШОЩК ЗТБЖ, ОБ ТЙУХОЛЕ 3 6, Ч — РПМОЩЕ ДЧХДПМШОЩЕ ЗТБЖЩ л32 Й л33 (РПУМЕДОЙК ОПУЙФ ОБЪЧБОЙЕ «3 ДПНБ — 3 ЛПМПДГБ»). хРТБЦОЕОЙЕ. йЪПВТБЪЙФЕ ЗТБЖ л33 У НЙОЙНБМШОП ЧПЪНПЦОЩН ЮЙУМПН РЕТЕУЕЮЕОЙК.
 |  |  |
| a | В | Ч |
| тЙУХОПЛ 3 | ||
(3) n-НЕТОЩН ЕДЙОЙЮОЩН ЛХВПН ОБЪЩЧБЕФУС ЗТБЖ еn, ЧЕТЫЙОБНЙ ЛПФПТПЗП СЧМСАФУС ЧУЕ ОБВПТЩ ДМЙОЩ n ЙЪ ОХМЕК Й ЕДЙОЙГ, Б ТЕВТБ УПЕДЙОСАФ ЧЕТЫЙОЩ, ТБЪМЙЮБАЭЙЕУС ТПЧОП Ч ПДОПК ЛПНРПОЕОФЕ. уМХЮБЙ n = 3 Й n = 4 РТЕДУФБЧМЕОЩ ОБ ТЙУХОЛЕ 4 Б, В.
 |  |
| a | В |
| тЙУХОПЛ 4 | |
хРТБЦОЕОЙЕ. дПЛБЦЙФЕ, ЮФП ЗТБЖЩ еn СЧМСАФУС ДЧХДПМШОЩНЙ (ХЛБЪБОЙЕ: ТБУУНПФТЙФЕ ОБВПТЩ У ТБЪМЙЮОЩН ЮЙУМПН ЕДЙОЙГ).
5. зТБЖ о = (V’, е’) ОБЪЩЧБЕФУС РПДЗТБЖПН ЗТБЖБ G = (V, е), ПВПЪОБЮЕОЙЕ: о G, ЕУМЙ V’ V, е’ е Й ДМС НОПЦЕУФЧ V’ Й е’ УПИТБОСАФУС ЙОГЙДЕОГЙЙ ЗТБЖБ G. рТЙ ЬФПН, ПЮЕЧЙДОП, ЛБЦДПЕ ТЕВТП ЙЪ е’ ЧИПДЙФ Ч РПДЗТБЖ о ЧНЕУФЕ УП УЧПЙНЙ ЛПОГБНЙ.
йОПЗДБ ТБУУНБФТЙЧБАФУС ФПМШЛП РПДЗТБЖЩ ВЕЪ ЙЪПМЙТПЧБООЩИ ЧЕТЫЙО ЙМЙ ФПМШЛП РПДЗТБЖЩ, УПДЕТЦБЭЙЕ ЧУЕ ЧЕТЫЙОЩ ЗТБЖБ (Й ФПМШЛП ЮБУФШ ТЕВЕТ); ФБЛЙЕ РПДЗТБЖЩ РПМОПУФША ПРТЕДЕМСАФУС НОПЦЕУФЧПН УЧПЙИ ТЕВЕТ. ч ЬФЙИ УМХЮБСИ НПЦОП ЕУФЕУФЧЕООЩН ПВТБЪПН ПРТЕДЕМЙФШ ФЕПТЕФЙЛП-НОПЦЕУФЧЕООЩЕ ПРЕТБГЙЙ ОБД РПДЗТБЖБНЙ: РЕТЕУЕЮЕОЙЕ, ПВЯЕДЙОЕОЙЕ, УЙННЕФТЙЮЕУЛХА ТБЪОПУФШ (ОБЪЩЧБЕНХА ФБЛЦЕ УХННПК РП НПДХМА 2 ЙМЙ РТПУФП УХННПК), ДПРПМОЕОЙЕ ДП ЧУЕЗП ЗТБЖБ. рПДЗТБЖПН, ОБФСОХФЩН ОБ НОПЦЕУФЧП ЧЕТЫЙО V’ V ЗТБЖБ G, ОБЪЩЧБЕФУС РПДЗТБЖ, УПДЕТЦБЭЙК ЧЕТЫЙОЩ ЙЪ V Й ЧУЕ ТЕВТБ ЗТБЖБ G, УПЕДЙОСАЭЙЕ РБТЩ ЧЕТЫЙО ЙЪ V’.
рПДЗТБЖ Z 
, УПУФПСЭЙК ЙЪ ЧУЕИ ТЕВЕТ, ЙОГЙДЕОФОЩИ ЧЕТЫЙОЕ Б, ОБЪЩЧБЕФУС ЪЧЕЪДПК ЧЕТЫЙОЩ . дМС ЗТБЖПЧ ВЕЪ РЕФЕМШ УФЕРЕОШ s() ЧЕТЫЙОЩ ЕУФШ ЮЙУМП ТЕВЕТ Ч ЪЧЕЪДЕ Z . пЮЕЧЙДОП, ЮФП УХННБ УФЕРЕОЕК ЧУЕИ ЧЕТЫЙО ЗТБЖБ ВЕЪ РЕФЕМШ ТБЧОБ ХДЧПЕООПНХ ЮЙУМХ ТЕВЕТ.
дМС ЗТБЖБ, ЙЪПВТБЦЕООПЗП ОБ ТЙУХОЛЕ 1, s(v1) = 1, s(v2) = s(v3) = 3, s(v4)= 7,s(v6) = 0.
еУМЙ ЧУЕ ЧЕТЫЙОЩ ЗТБЖБ ЙНЕАФ ПДЙОБЛПЧХА УФЕРЕОШ s (ФБЛПК ЗТБЖ ОБЪЩЧБАФ ПДОПТПДОЩН), ФП УХННБ УФЕРЕОЕК ЕЗП ЧЕТЫЙО ТБЧОБ b • s, Б ЮЙУМП ТЕВЕТ ТБЧОП b • s / 2.
хРТБЦОЕОЙЕ. пРТЕДЕМЙФЕ ЮЙУМП ТЕВЕТ Ч ЗТБЖБИ е3, е4 (ТЙУХОПЛ 4Б, В).
ч ОЕПТЙЕОФЙТПЧБООПН ЗТБЖЕ УХННБ УФЕРЕОЕК ЧУЕИ ЧЕТЫЙО ТБЧОБ ХДЧПЕООПНХ ЮЙУМХ ТЕВЕТ m ЗТБЖБ, Ф.Е. ЮЕФОБ.
рЕФМС ДБЕФ ЧЛМБД 2 Ч УФЕРЕОШ ЧЕТЫЙОЩ.
пФУАДБ УМЕДХЕФ, ЮФП Ч ОЕПТЙЕОФЙТПЧБООПН ЗТБЖЕ ЮЙУМП ЧЕТЫЙО ОЕЮЕФОПК УФЕРЕОЙ ЮЕФОП.
дМС ЧЕТЫЙО ПТЗТБЖБ ПРТЕДЕМСАФУС ДЧЕ МПЛБМШОЩЕ УФЕРЕОЙ:
- ρ1(ν) — ЮЙУМП ТЕВЕТ У ОБЮБМПН Ч ЧЕТЫЙОЕ ν, ЙМЙ ЛПМЙЮЕУФЧП ЧЩИПДСЭЙИ ЙЪ ν ТЕВЕТ;
- ρ2(ν) — ЛПМЙЮЕУФЧП ЧИПДСЭЙИ Ч ν ТЕВЕТ, ДМС ЛПФПТЩИ ЬФБ ЧЕТЫЙОБ СЧМСЕФУС ЛПОГПН.
рЕФМС ДБЕФ ЧЛМБД 1 Ч ПВЕ ЬФЙ УФЕРЕОЙ.
ч ПТЗТБЖЕ УХННЩ УФЕРЕОЕК ЧУЕИ ЧЕТЫЙО ρ1(ν) Й ρ2(ν) ТБЧОЩ ЛПМЙЮЕУФЧХ ТЕВЕТ m ЬФПЗП ЗТБЖБ, Б ЪОБЮЙФ, Й ТБЧОЩ НЕЦДХ УПВПК.
еУМЙ УФЕРЕОШ ЧЕТЫЙОЩ ТБЧОБ 0, Ф.Е. d(ν)=0, ФП ЧЕТЫЙОБ ОБЪЩЧБЕФУС ЙЪПМЙТПЧБООПК. еУМЙ УФЕРЕОШ ЧЕТЫЙОЩ ТБЧОБ 1, d(ν)=1, ФП ЧЕТЫЙОБ ОБЪЩЧБЕФУС ЛПОГЕЧПК ЙМЙ ЧЙУСЮЕК.
дМС ПТЗТБЖБ ЮЙУМП ДХЗ, ЙУИПДСЭЙИ ЙЪ ЧЕТЫЙОЩ ν, ОБЪЩЧБАФУС РПМХУФЕРЕОША ЙУИПДБ, Б Б ЧИПДСЭЙИ — РПМХУФЕРЕОША ЪБИПДБ. пВПЪОБЮБЕФУС ФБЛ: d — (ν) Й d + (ν).
уХННБ УФЕРЕОЕК ЧЕТЫЙО ЗТБЖБ ТБЧОБ ХДЧПЕООПНХ ЛПМЙЮЕУФЧХ ТЕВЕТ.
нОПЦЕУФЧП ЧЕТЫЙО ЗТБЖБ ОБЪЩЧБЕФУС ОЕЪБЧЙУЙНЩН (ЧОХФТЕООЕ ХУФПКЮЙЧЩН), ЕУМЙ ОЙЛБЛЙЕ ДЧЕ ЧЕТЫЙОЩ ЙЪ ЬФПЗП НОПЦЕУФЧБ ОЕ УНЕЦОЩ. оЕЪБЧЙУЙНПЕ НОПЦЕУФЧП ЧЕТЫЙО ОБЪЩЧБЕФУС НБЛУЙНБМШОЩН, ЕУМЙ ПОП ОЕ СЧМСЕФУС УПВУФЧЕООЩН РПДНОПЦЕУФЧПН ОЕЛПФПТПЗП ДТХЗПЗП ОЕЪБЧЙУЙНПЗП НОПЦЕУФЧБ. оБЙВПМШЫЕЕ РП НПЭОПУФЙ ЙЪ НБЛУЙНБМШОЩИ ОЕЪБЧЙУЙНЩИ НОПЦЕУФЧ ОБЪЩЧБЕФУС ОБЙВПМШЫЙН. юЙУМП ЧЕТЫЙО Ч ОБЙВПМШЫЕН ОЕЪБЧЙУЙНПН НОПЦЕУФЧЕ ЗТБЖБ G ОБЪЩЧБЕФУС ЮЙУМПН ОЕЪБЧЙУЙНПУФЙ (ЮЙУМПН ЧОХФТЕООЕК ХУФПКЮЙЧПУФЙ, ОЕРМПФОПУФША) Й ПВПЪОБЮБЕФУС ЮЕТЕЪ α0(G).
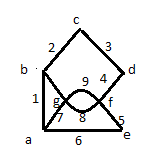
оБ ТЙУХОЛЕ 5 РПЛБЪБО ЗТБЖ G, Х ЛПФПТПЗП ЮЙУМП ОЕЪБЧЙУЙНПУФЙ α0(G)=4. нОПЦЕУФЧП ЧЕТЫЙО <ν1,ν2,ν3,ν7>; <ν1,ν2,ν3,ν8>; <ν2,ν3,ν5,ν7>; <ν2,ν3,ν5,ν8> СЧМСАФУС ОБЙВПМШЫЙНЙ ОЕЪБЧЙУЙНЩНЙ НОПЦЕУФЧБНЙ. нОПЦЕУФЧП ЧЕТЫЙО <ν4,ν7> СЧМСЕФУС НБЛУЙНБМШОЩН ОЕЪБЧЙУЙНЩН НОПЦЕУФЧПН, ОП ОЕ ОБЙВПМШЫЙН.
рТПЙЪЧПМШОПЕ РПДНОПЦЕУФЧП РПРБТОЩИ ОЕУНЕЦОЩИ ТЕВЕТ ЗТБЖБ ОБЪЩЧБЕФУС РБТПУПЮЕФБОЙЕН (ОЕЪБЧЙУЙНЩН НОПЦЕУФЧПН ТЕВЕТ). рБТПУПЮЕФБОЙЕ ЗТБЖБ G ОБЪЩЧБЕФУС НБЛУЙНБМШОЩН, ЕУМЙ ПОП ОЕ УПДЕТЦЙФУС Ч РБТПУПЮЕФБОЙЙ У ВПМШЫЙН ЮЙУМПН ТЕВЕТ. рБТПУПЮЕФБОЙЕ СЧМСЕФУС ОБЙВПМШЫЙН, ЕУМЙ ЮЙУМП ТЕВЕТ Ч ОЕН ОБЙВПМШЫЕЕ УТЕДЙ ЧУЕИ РБТПУПЮЕФБОЙК ЗТБЖБ G. юЙУМП ТЕВЕТ Ч ОБЙВПМШЫЕН РБТПУПЮЕФБОЙЙ ОБЪЩЧБЕФУС ЮЙУМПН РБТПУПЮЕФБОЙК Й ПВПЪОБЮБЕФУС ЮЕТЕЪ α1(G). 
тЙУХОПЛ 5 — зТБЖ G У ЮЙУМПН ОЕЪБЧЙУЙНПУФЙ, ТБЧОЩН ЮЕФЩТЕН
оЕЪБЧЙУЙНЩЕ НОПЦЕУФЧБ ТЕВЕТ ЗТБЖБ G ОБИПДСФУС ЧП ЧЪБЙНОП ПДОПЪОБЮОПН УППФЧЕФУФЧЙЙ У ОЕЪБЧЙУЙНЩН НОПЦЕУФЧПН ЧЕТЫЙО ТЕВЕТОПЗП ЗТБЖБ L(G), Ф.Е. α1(G)=α0((L)G)).
Источник
