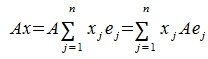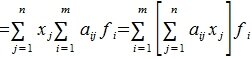Способы задания линейного оператора

9. Линейные операторы

9.1. Основные понятия и способы задания линейных операторов

Дано V – векторное пространство над полем P, dim V = n.

Определение 9.1. Говорят, что задано отображение  множества V в себя, если каждому элементу x из V поставлен в соответствие единственный элемент y, тоже принадлежащий V. При этом приняты следующие обозначения и термины: : V  V, : х  y, (х) = y; элемент x – прообраз элемента y, y – образ x.

Определение 9.2. Линейным оператором пространства V называется отображение : V  V такое, что  a, b  V,    Р

Вместо «линейный оператор» говорят также «линейное отображение» или «отображение, сохраняющее операции сложения и умножения на элемент поля»

Пример 9.1. 1) В произвольном векторном пространстве V зададим отображение следующей формулой: (х) = kх. Это отображение является линейным оператором и называется оператором гомотетии.

Если k = 1, то отображение примет вид: (х) = 1. Его называют тождественным оператором и обозначают буквой : (х) = х.

2) В пространстве V = R 2  2 оператор транспонирования задают формулой (А) = А t , где А t – матрица, транспонированная для матрицы А.

3) В пространстве V = R[x]_(n) (многочленов степени, не превосходящей n) можно задать отображение , ставящее в соответствие произвольному многочлену его производную, т. е. : f(x)  f ‘(x), (f ) = f ‘. Покажем, что это отображение линейно:

Способы задания линейных операторов

Приведенные примеры не показывают, сколько в каждом векторном пространстве существует линейных операторов, каким способом их можно задавать. Ответом на эти вопросы является следующая теорема.

Теорема 9.1. Для того чтобы задать линейный оператор, достаточно задать образы базисных векторов.

Покажем, как найти образ произвольного вектора x. Разложим вектор x по базисным векторам и найдем его образ, используя свойства линейного отображения:

Пусть в векторном пространстве V задан линейный оператор , т. е. указаны образы базисных векторов (e₁), (e₂), …, (e_n). Разложим эти векторы по векторам базиса:

Используем координаты образов базисных векторов.

Определение 9.3. Матрицей линейного оператора в данном базисе называется матрица, составленная из координат образов базисных векторов, записанных в столбцы.

M() = , M()  Р n  n .

Если зафиксировать базис пространства V, то каждому линейному оператору  ставится в соответствие единственная квадратная матрица порядка:   M().

Верно и обратное: по произвольной квадратной матрице A единственным образом можно задать линейный оператор , взяв за координаты образов базисных векторов столбцы матрицы A.

Пример 9.2. 1) В пространстве V размерности 3 найти матрицу оператора гомотетии.

[(e₁)] = , [(e₂)] = , [(e₃)] = .

Составляем матрицу : M() = . В частности, получаем матрицы тождественного и нулевого операторов: M() = = Е, M() = = О.

Решение. Найдем образы базисных векторов, их координаты и составим матрицу линейного оператора.

[(e₁)] = , [(e₂)] = , [(e₃)] = ,[(e₄)] = ;M() = .

Источник

Линейные операторы

1. Понятие линейного оператора

Пусть R и S линейные пространства, которые имеют размерность n и m соответственно. Оператором A действующим из R в S называется отображение вида , сопоставляющее каждому элементу x пространства R некоторый элемент y пространства S. Для этого отображения будем использовать обозначение y= A(x) или y= Ax.

Определение 1. Оператор A действующий из R в S называется линейным, если для любых элементов x₁ и x₂ пространства R и любого λ из числового поля K выполняются соотношения

Если пространство S совпадает с пространством R, то линейный оператор, который действует из R в R называют линейным преобразованием пространства R.

Пусть заданы два векторных пространства n-мерный R и m-мерный S, и пусть в этих пространствах заданы базисы и соответственно. Пусть задано отображение

где A — m×n -матрица с коэффициентами из поля K. Тогда каждому элементу из R соответствует элемент y=Ax из S. Отображение (1) определяет оператор A. Покажем, что этот оператор обладает свойством линейности. Действительно, учитывая свойства умножения матриц, можно записать:

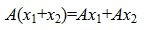,	(2)
.

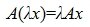Покажем теперь обратное, т.е. что для любого линейного оператора A, отображающего пространство R в S и произвольных базисов и в R и S соответственно, существует такая матрица A с элементами из численного поля K, что определяемое этой матрицей линейное отображение (1) выражает координаты отображенного вектора y через координаты исходного вектора x.

Пусть x − произвольный элемент в R. Тогда

(3)

является разложением x в по базису .

Применим оператор A к базисным векторам :

(4)

где a_ij − координаты полученного вектора в базисе .

Тогда применяя оператор A к элементу x и учитывая (3) и (4), имеем

Сделаем следующее обозначение:

(6)

Тогда равенство (5) примет следующий вид:

(7)

Из равенства (7) следует, что любой элемент из пространства R при отображении оператором A, в пространстве S и в базисе имеет координаты y_i, i=1,2. m. В свою очередь, из (6) следует, что этим координатам соответствуют линейные комбинации координатов элемента x_j, j=1,2. n с коэффициентами a_ij i=1,2. m; j=1,2. n.

Построим матрицу A с элементами a_ij:

(8)

Тогда выражение (6) можно записать в матричном виде:

Матрица A называется матрицей линейного оператора в заданных базисах и .

2. Сложение линейных операторов

Пусть A и B два линейных оператора действующих из R в S и пусть A и B — mxn − матрицы соответствующие этим операторам.

Определение 2. Суммой линейных операторов A и B называется оператор C, определяемый равенством

Cx= Ax+ Bx, x∈R,

(10)

где x∈R означает, что x принадлежит пространстве R.

Сумма линейных операторов обозначается так C=A+B. Легко убедится, что сумма линейных операторов также является линейным оператором.

Применим оператор C к базисному вектору e_j, тогда:

Cej= Aej+ Bej=	n	(aij+bij) ej
	∑
	j= 1

Следовательно оператору C отвечает матрица ,где i=1,2. m, j=1,2. n, т.е.

3. Умножение линейных операторов

Пусть заданы три линейных пространства R, S и T. Пусть линейный оператор B отображает R в S, а линейный оператор A отображает S в T.

Определение 3. Произведением операторов A и B называется оператор C, для которого выполняется следующее равенство при любом x из R:

Cx= A( Bx), x ∈ R.

(12)

Произведение линейных операторов обозначается C=AB. Легко убедится, что произведение линейных операторов также является линейным оператором.

Таким образом оператор C отображает пространство R в T. Выберем в пространствах R, S и T базисы и обозначим через A, B и C матрицы операторов A, B и C соответствующие этим базисам. Тогда отображения линейных операторов A, B, C

y=Bx, z=Ay, z=Cx

можно записать в виде матричных равенств

y=Bx, z=Ay, z=Cx

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Cx=A(Bx)=(AB)x.

Учитывая произвольность х, получим

Следовательно произведению операторов C=AB соответствует матричное произведение C=AB.

4. Умножение линейного оператора на число

Пусть задан линейный оператор A отображающий R в S и некоторое число λ из поля K.

Определение 4. Произведением оператора A на число λ называется оператор C, для которого выполняется следующее равенство при любом x из R:

Cx=λ ( Ax)

(14)

Таким образом оператор C отображает пространство R в S. Выберем в пространствах R и S базисы и обозначим через A матрицу оператора A соответствующее этим базисам векторные равенства

y=Ax, z=λy, z=Cx

можно записать в виде матричных равенств

y=Ax, z=λy, z=Cx

где x, y, z − векторы x, y, z − представленные в виде координатных столбцов. Тогда

Cx=λ(Ax)=(λA)x.

Учитывая произвольность х, получим

Следовательно произведению оператора C на число λ соответствует произведение матрицы A на число λ.

5. Нулевой оператор

Оператор, отображающий все элементы пространства R в нулевой элемент пространства S называется нулевым оператором и обозначается через O. Действие нулевого оператора можно записать так:

6. Противоположный оператор

Противоположным оператору A называется оператор −A удовлетворяющий равенству:

7. Ядро линейного оператора

Определение 5. Ядром линейного оператора A называется множество всех тех элементов x пространства R, для которых выполняется следующее равенство: Ax=0.

Ядро линейного оператора также называют дефектом оператора. Ядро линейного оператора обозначается символом ker A.

8. Образ линейного оператора

Определение 6. Образом линейного оператора A называется множество всех элементов y пространства R, для которых выполняется следующее равенство: y=Ax для всех x из R.

Образ линейного оператора обозначается символом im A.

9. Ранг линейного оператора

Определение 7. Рангом линейного оператора A обозначаемое символом rang A называется число равное размерности образа im A оператора A, т.е.: rang A=dim(im A).

Источник