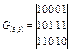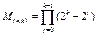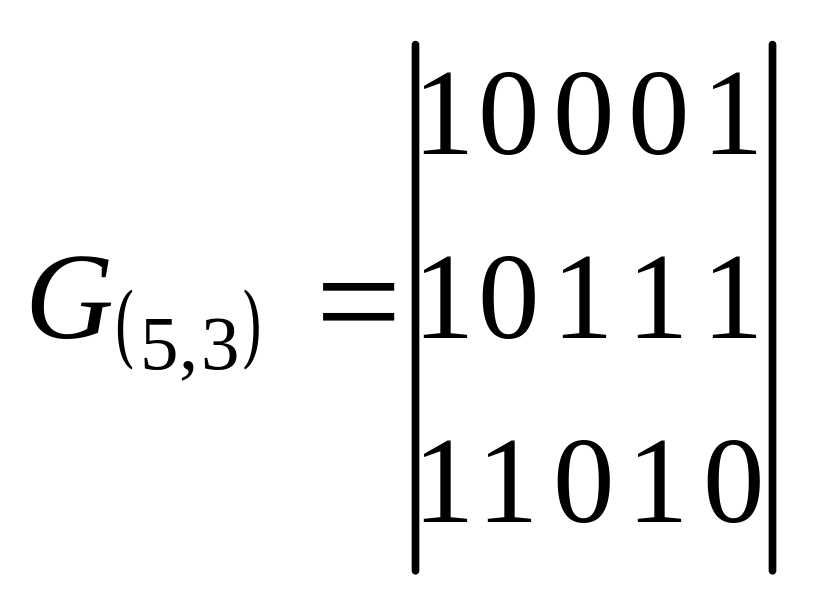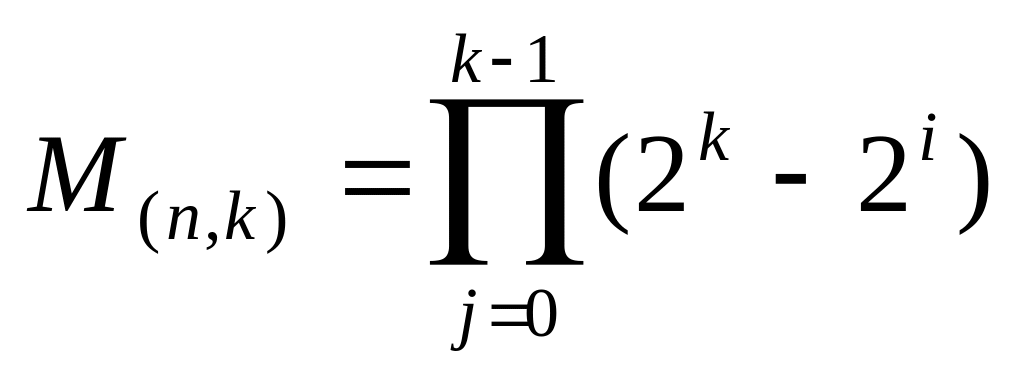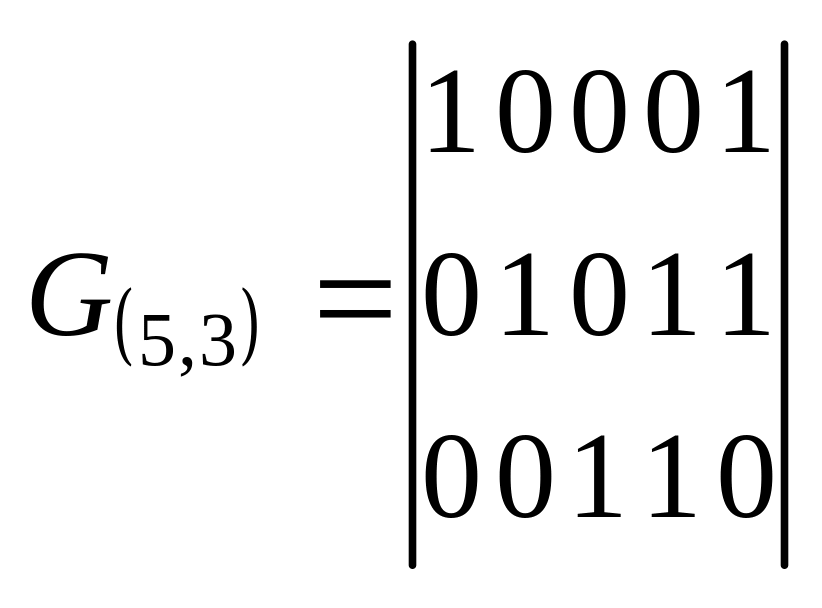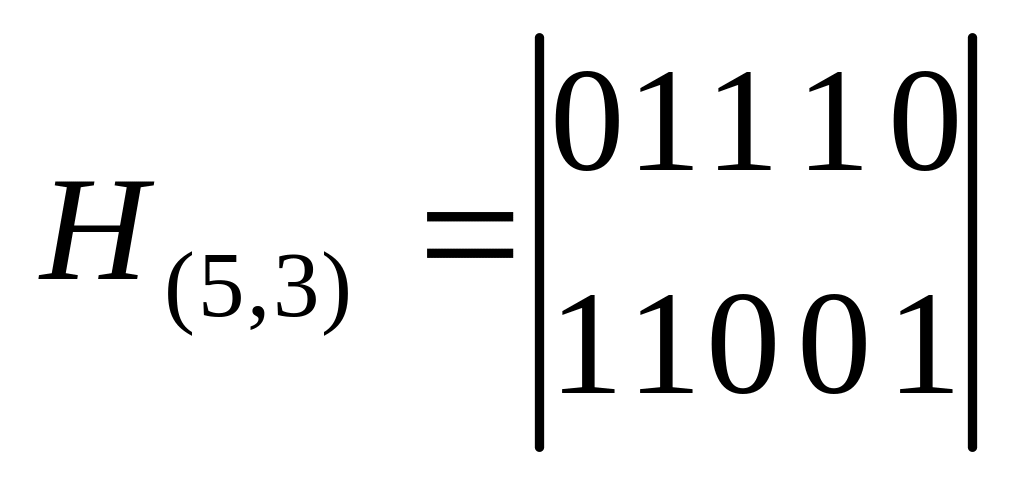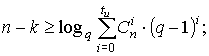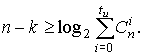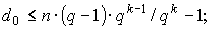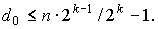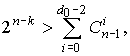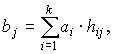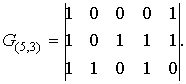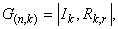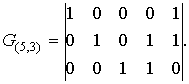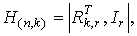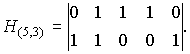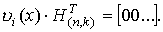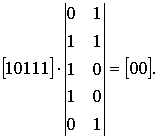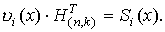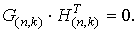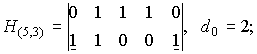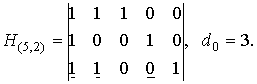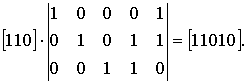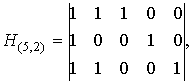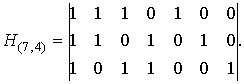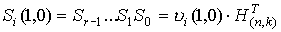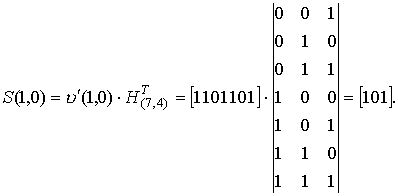Способы задания линейных кодов
1. Перечислением кодовых слов, т.е. составлением списка всех кодовых слов кода.
Пример. В таблице справа представлены все кодовые слова (5,3)-кода (ai — информационные, а bi — проверочные символы).
| № п/п | a1 | a2 | a3 | b1 | b2 |
2. Системой проверочных уравнений, определяющих правила формирования проверочных символов по известным информационным:
, где
j ‑ номер проверочного символа;
i ‑ номер информационного символа;
hij ‑ коэффициенты, принимающие значения 0 или 1 в соответствии с правилами формирования конкретных групповых кодов.
Пример. Для кода (5,3) проверочные уравнения имеют вид:
3. Матричное, основанное на построении порождающей и проверочной матриц.
Векторное пространство Vn над GF(2) включает в себя 2 n векторов (n-последовательностей), а подпространством его является множество из 2 k кодовых слов длины n, которое однозначно определяется его базисом, состоящим из k линейно независимых векторов. Поэтому линейный (n, k) — код полностью определяется набором из k кодовых слов, принадлежащих этому коду.
Набор из k кодовых слов, соответствующих базису, обычно представляется в виде матрицы, которая называется порождающей.
Пример. (5,3) — код, который был представлен в таблице 1, может быть задан матрицей 
Остальные кодовые слова получаются сложением строк матриц в различных сочетаниях.
Общее количество различных вариантов порождающих матрицу определяется выражением 
Для исключения неоднозначности в записи G(n, k) вводят понятие о канонической или систематической форме матрицы, которая имеет вид
, где Ik ‑ единичная матрица, содержащая информационные символы; Rk,r ‑ прямоугольная матрица, составленная из проверочных символов.
Пример. Порождающая матрица в систематическом виде для (5,3) – кода 
Порождающая матрица G(n,k) в систематическом виде может быть получена из любой другой матрицы посредством элементарных операций над строками (перестановкой двух произвольных строк, заменой произвольной строки на сумму ее самой и ряда других) и дальнейшей перестановкой столбцов.
Проверочная матрица в систематическом виде имеет вид 
, где Ir ‑ единичная матрица; 
‑ прямоугольная матрица в транспонированном виде матрицы Rk,r из порождающей матрицы.
Пример. Проверочная матрица (5,3) – кода 
Источник
Способы задания линейного кода
Способы задания линейного кода определяют структуру кодера, который для систематических кодов должен по известным информационным битам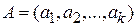 
найти проверочные 
и сформировать кодовое слово 
.
Способы задания линейного кодаесть способы задания линейного подпространства размерности k в пространстве размерности n.
Вектор, принадлежащий подпространству, имеет только k независимых координат, а остальные зависимы от них. Поэтому каждый проверочный бит bi есть линейная комбинация некоторых, вполне определенных информационных, например bi = a1 + a3 + a6. Благодаря свойствам сложения по модулю 2 последовательность a1, a3, a6, bi содержит четное число 1. Поэтому bi часто называют битами контроля четности. Для задания кода такие соотношения должны быть определены для всех контрольных бит.
Любое подпространство (код) может быть задано с помощью базиса, содержащего k линейно независимых векторов (кодовых слов). Базисов существует много.
Построим матрицу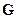 
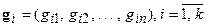
размерности 
, строками которой служат кодовые слова 
:
. (6.1)
Представив информационное сообщение в виде 
–компонентного вектора 
, произвольное слово 
линейного кода может быть записано в виде
. (6.2)
Кодовое слово представляет собой результат произведения информационного вектора 
на матрицу , которую по этой причине называют порождающей матрицей линейного кода. Следует особо подчеркнуть, что согласно аксиомам векторного пространства:
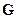
– любой линейный код содержит нулевое кодовое слово 
;
– любая сумма слов линейного кода вновь дает кодовое слово, принадлежащее данному коду.
Любой линейный код всегда может быть преобразован в эквивалентный (т.е. обладающий аналогичными параметрами 
), которому отвечает каноническая (стандартная) порождающая матрица
, (6.3)
где 
– 
единичная матрица, а 
– матрица размерности 
. Использование канонической порождающей матрицы позволяет построить систематический линейный код, в котором информационные символы занимают первые позиций кодовых слов:
, (6.4)
где 
– проверочные символы кодового слова.
Таким образом, кодер, построенный на основе порождающей матрицы, должен содержать генератор базисных векторов и сумматоры по модулю 2 для формирования слов согласно (6.2).
С каждым линейным подпространством связана матрица H, содержащая n столбцов и n – k строк и проектирующая любое кодовое слово на перпендикуляр к этому подпространству. Поэтому для любого кодового слова справедливо
,
где нулевой вектор содержит 
разрядов, а индекс T означает транспонирование матрицы, чтобы матричное произведение было выполнимо.
Это свойство использует декодер для проверки: принадлежит ли наблюдаемый на выходе канала сигнал коду или нет. Поэтому матрица H называется проверочной.
Таким образом, линейный код может быть задан как порождающей и проверочной матрицами, так и соотношениями, устанавливающими связь между проверочными и информационными символами кодовых слов.
Пример.
Дата добавления: 2015-04-20 ; просмотров: 21 | Нарушение авторских прав
Источник
Способы задания линейных кодов
1. Перечислением кодовых слов, т.е. составлением списка всех кодовых слов кода.
Пример. В таблице справа представлены все кодовые слова (5,3)-кода (ai — информационные, а bi — проверочные символы).
2. Системой проверочных уравнений, определяющих правила формирования проверочных символов по известным информационным:
, где
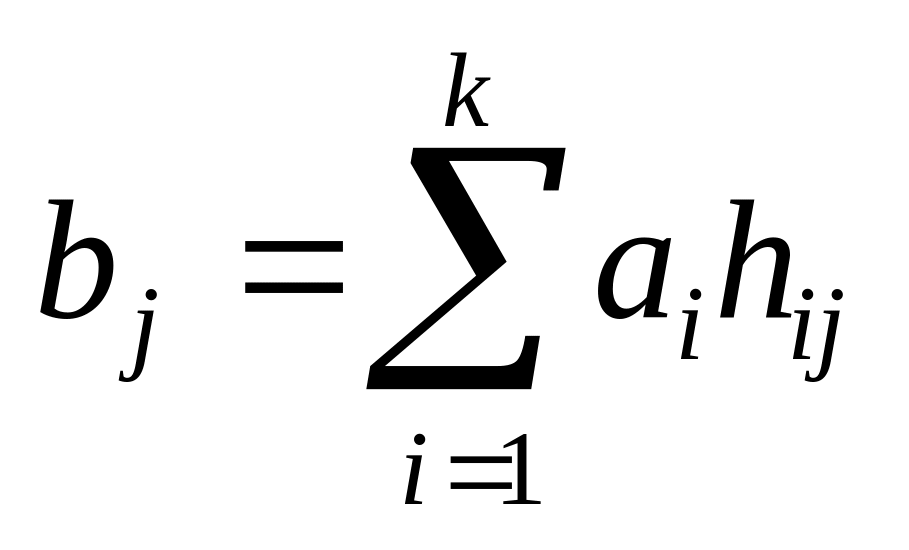
j ‑ номер проверочного символа;
i ‑ номер информационного символа;
hij ‑ коэффициенты, принимающие значения 0 или 1 в соответствии с правилами формирования конкретных групповых кодов.
Пример. Для кода (5,3) проверочные уравнения имеют вид:
3. Матричное, основанное на построении порождающей и проверочной матриц.
Векторное пространство Vn над GF(2) включает в себя 2 n векторов (n-последовательностей), а подпространством его является множество из 2 k кодовых слов длины n, которое однозначно определяется его базисом, состоящим из k линейно независимых векторов. Поэтому линейный (n, k) — код полностью определяется набором из k кодовых слов, принадлежащих этому коду.
Набор из k кодовых слов, соответствующих базису, обычно представляется в виде матрицы, которая называется порождающей.
Пример. (5,3) — код, который был представлен в таблице 1, может быть задан матрицей 
Остальные кодовые слова получаются сложением строк матриц в различных сочетаниях.
Общее количество различных вариантов порождающих матрицу определяется выражением 
Для исключения неоднозначности в записи G(n, k) вводят понятие о канонической или систематической форме матрицы, которая имеет вид
, где Ik ‑ единичная матрица, содержащая информационные символы; Rk,r ‑ прямоугольная матрица, составленная из проверочных символов.
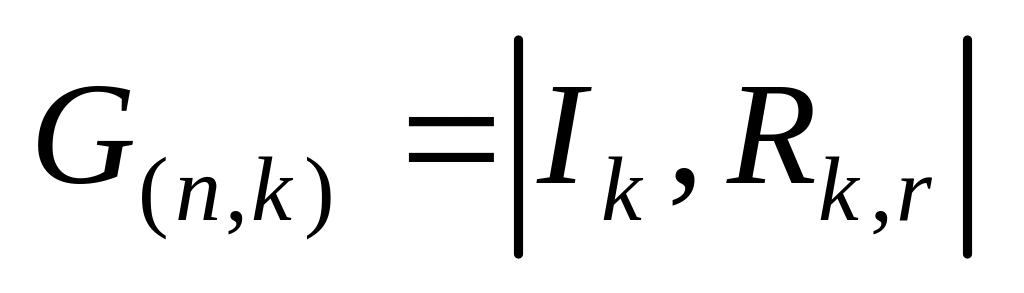
Пример. Порождающая матрица в систематическом виде для (5,3) – кода 
Порождающая матрица G(n,k) в систематическом виде может быть получена из любой другой матрицы посредством элементарных операций над строками (перестановкой двух произвольных строк, заменой произвольной строки на сумму ее самой и ряда других) и дальнейшей перестановкой столбцов.
Проверочная матрица в систематическом виде имеет вид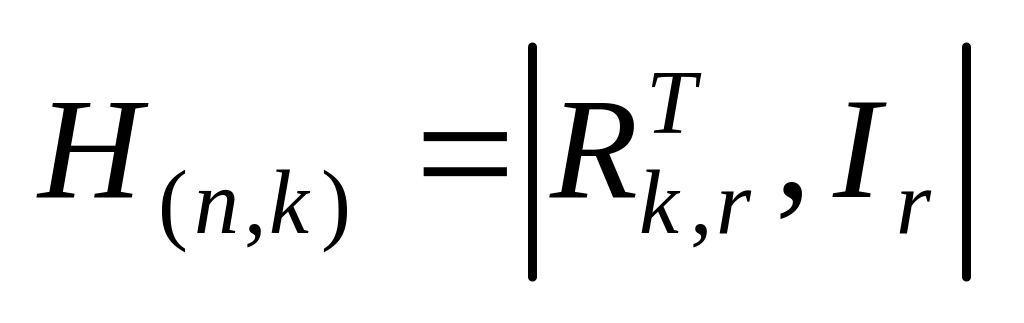 
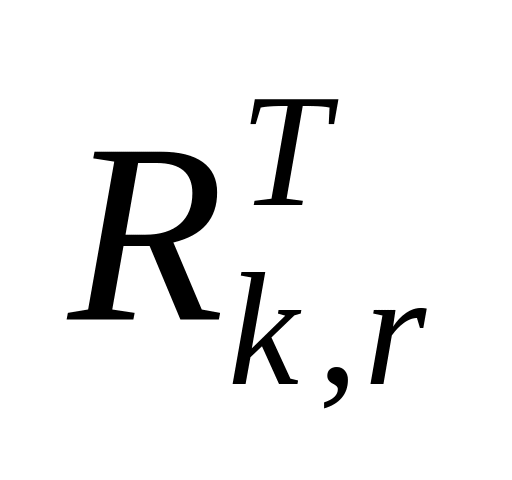
, где Ir ‑ единичная матрица; 
‑ прямоугольная матрица в транспонированном виде матрицы Rk,r из порождающей матрицы.
Пример. Проверочная матрица (5,3) – кода 
Источник
Способы задания линейного кода
1. Помехоустойчивые коды и их основные параметры
Проблема повышения верности обусловлена не соответствием между требованиями, предъявляемыми при передачи данных и качеством реальных каналов связи. В сетях передачи данных требуется обеспечить верность не хуже 10 -6 — 10 -9 , а при использовании реальных каналов связи и простого (первичного) кода указанная верность не превышает .
Одним из путей решения задачи повышения верности в настоящее время является использование специальных процедур, основанных на применении помехоустойчивых (корректирующих) кодов.
1.1 Принцип построения помехоустойчивых кодов
Простые коды характеризуются тем, что для передачи информации используются все кодовые слова (комбинации), количество которых равно N=q n (q — основание кода, а n — длина кода). В общем случае они могут отличаться друг от друга одним символом (элементом). Поэтому даже один ошибочно принятый символ приводит к замене одного кодового слова другим и, следовательно, к неправильному приему сообщения в целом.
Помехоустойчивыми называются коды, позволяющие обнаруживать и (или) исправлять ошибки в кодовых словах, которые возникают при передаче по каналам связи. Эти коды строятся таким образом, что для передачи сообщения используется лишь часть кодовых слов, которые отличаются друг от друга более чем в одном символе. Эти кодовые слова называются разрешенными. Все остальные кодовые слова не используются и относятся к числу запрещенных.
Применение помехоустойчивых кодов для повышения верности передачи данных связанно с решением задач кодирования и декодирования.
Задача кодирования заключается в получении при передаче для каждой k — элементной комбинации из множества q k соответствующего ей кодового слова длиною n из множества q n .
Задача декодирования состоит в получении k — элементной комбинации из принятого n — разрядного кодового слова при одновременном обнаружении или исправлении ошибок.
1.2 Основные параметры помехоустойчивых кодов
Длина кода — n;
Длина информационной последовательности — k;
Длина проверочной последовательности — r=n-k;
Кодовое расстояние кода — d0;
Скорость кода — R=k/n;
Избыточность кода — R ў ;
Вероятность обнаружения ошибки (искажения) — РОО;
Вероятность не обнаружения ошибки (искажения) — РНО.
Кодовое расстояние между двумя кодовыми словами (расстояние Хэмминга) — это число позиций, в которых они отличаются друг от друга.
Кодовое расстояние кода — это наименьшее расстояние Хэмминга между различными парами кодовых слов.
Основные зависимости между кратностью обнаруживаемых ошибок t0, исправляемых ошибок tu, исправлением стираний tc и кодовым расстоянием d0 кода:
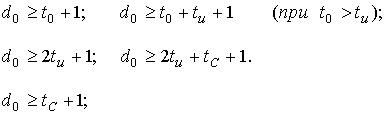
Стиранием называется «потеря» значения передаваемого символа в некоторой позиции кодового слова, которая известна.
Код, в котором каждое кодовое слово начинается с информационных символов и заканчивается проверочными символами, называется систематическим.
1.3 Граничные соотношения между параметрами помехоустойчивых кодов
Одной из важнейших задач построения помехоустойчивых кодов с заданными характеристиками является установление соотношения между его способностью обнаруживать или исправлять ошибки и избыточностью.
Существуют граничные оценки, связывающие d0, n и k.
Граница Хэмминга, которая близка к оптимальной для высоко скоростных кодов, определяется соотношениями:
для q-ного кода 
для двоичного кода 
Граница Плоткина, которую целесообразно использовать для низкоскоростных кодов определяется соотношениями:
для q-ного кода 
для двоичного кода 
Границы Хэмминга и Плоткина являются верхними границами для кодового расстояния при заданных n и k, задающими минимальную избыточность, при которой существует помехоустойчивый код, имеющий минимальное кодовое расстояние и гарантийно исправляющий tu — кратные ошибки.
Граница Варшамова-Гильберта (нижняя граница), определяемая соотношениями: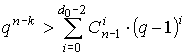 
и 
показывает, при каком значении n-k определено существует код, гарантийно исправляющий ошибки кратности tu.
2. Линейные блоковые коды
Линейным блоковым (n,k) — кодом называется множество N последовательностей длины n над GF(q), называемых кодовыми словами, которое характеризуется тем, что сумма двух кодовых слов является кодовым словом, а произведение любого кодового слова на элемент поля также является кодовым словом.
Обычно N=q k , где k — некоторое целое число.
Если q=2, линейные коды называются групповыми, так как кодовые слова образуют математическую структуру, называемую группой. При формирование этого кода линейной операцией является суммирование по mod2.
2.1 Способы задания линейных кодов
1. Перечислением кодовых слов, т.е. составлении списка всех кодовых слов кода.
Пример. В таблице 1 представлены все кодовые слова (5,3) — кода (ai — информационные, а bi — проверочные символы).
Таблица 1
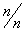
2. Системой проверочных уравнений, определяющих правила формирования проверочных символов по известным информационным:
где
j — номер проверочного символа;
i — номер информационного символа;
hij — коэффициенты, принимающие значения 0 или 1 в соответствии с правилами формирования конкретных групповых кодов.
Пример. Для кода (5,3) проверочные уравнения имеют вид:
b1= a2 + a3;
b2= a1 + a2.
3. Матричное, основанное на построении порождающей и проверочной матриц.
Векторное пространство Vn над GF(2) включает в себя 2 n векторов (n-последовательностей), а подпространством его является множество из 2 k кодовых слов длины n, которое однозначно определяется его базисом, состоящим из k линейно независимых векторов. Поэтому линейный (n,k) — код полностью определяется набором из k кодовых слов, принадлежащих этому коду.
Набор из k кодовых слов, соответствующих базису, обычно представляется в виде матрицы, которая называется порождающей.
Пример. (5,3) — код, который был представлен в таблице 1, может быть задан матрицей
Остальные кодовые слова получаются сложением строк матриц в различных сочетаниях.
Общее количество различных вариантов порождающих матрицу определяется выражением
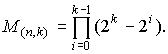
Для исключения неоднозначности в записи G(n,k) вводят понятие о канонической или систематической форме матрицы, которая имеет вид
где
Ik — единичная матрица, содержащая информационные символы;
Rk,r — прямоугольная матрица, составленная из проверочных символов.
Пример. Порождающая матрица в систематическом виде для (5,3) — кода
Порождающая матрица G(n,k) в систематическом виде может быть получена из любой другой матрицы посредством элементарных операций над строками (перестановкой двух произвольных строк, заменой произвольной строки на сумму ее самой и ряда других) и дальнейшей перестановкой столбцов.
Проверочная матрица в систематическом виде имеет вид
где Ir — единичная матрица;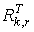 
— прямоугольная матрица в транспонированном виде матрицы Rk,r из порождающей матрицы.
Пример. Проверочная матрица (5,3) — кода
2.2 Основные свойства линейных кодов
1. Произведение любого кодового слова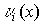 
на транспонированную проверочную матрицу дает нулевой вектор размерности (n-k)
Пример. для кода (5,3)
2. Произведение некоторого кодового слова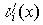
, т.е. с ошибкой, на транспонированную проверочную матрицу называется синдромом и обозначается Si(x)
3. Между порождающей и проверочной матрицами в систематическом виде существует однозначное соответствие, а именно:
4. Кодовое расстояние d0 (n,k) — кода равно минимальному числу линейно зависимых столбцов проверочной матрицы
Пример.
для кода (5,3):
для кода (5,2):
5. Произведение информационного слова на порождающую матрицу дает кодовое слово кода
Пример. для кода (5,3)
6. Два кода называются эквивалентными, если их порождающие матрицы отличаются перестановкой координат, т.е. порождающие матрицы получаются одна за другой перестановкой столбцов и элементарных операций над строками.
7. Кодовое расстояние любого линейного (n,k) — кода удовлетворяет неравенству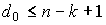 
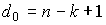
(граница Сингтона). Линейный (n,k) — код, удовлетворяющий равенству
, называется кодом с максимальным расстоянием.
2.3 Стандартное расположение группового кода
Стандартное расположение группового кода представляет разложение множества всех возможных n-элементных слов, представляющих собой группу, на смежные классы по подгруппе из 2 k кодовых слов, составляющих (n,k)-код (см. таблицу 2).
Таблица 2
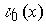
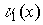
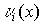
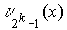
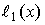
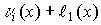
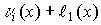
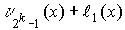
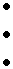
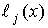
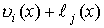
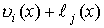
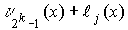
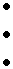
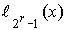
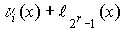
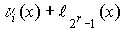
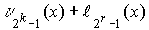
Образующие или лидеры смежных классов выбираются таким образом, чтобы в их состав вошли наиболее вероятные образцы ошибок в кодовом слове, т.е. образцы ошибок с наименьшим весом.
Пример. Код (5,3) имеет матрицы
и 
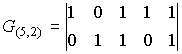
а стандартное расположение имеет вид,
| 00000 | 10111 | 01101 | 11010 |
| 00001 | 10110 | 01100 | 11011 |
| 00010 | 10101 | 01111 | 11000 |
| 00100 | 10011 | 01001 | 11110 |
| 01000 | 11111 | 00101 | 10010 |
| 10000 | 00111 | 11101 | 01010 |
| 00011 | 10100 | 01110 | 11001 |
| 10001 | 00110 | 11100 | 01011 |
Этот код имеет d0=3. Он гарантирует исправление одиночных ошибок, конфигурация которых дана в первом столбце.
Процедура исправления ошибок следующая. Принятое кодовое слово анализируют и определяют, в каком столбце оно находится, а затем в качестве исправленного кодового слова берут слово, находящееся в верхней строке.
Однако, если длина кода большая и таблица стандартного расположения также значительная, пользоваться таким алгоритмом неудобно. Поэтому при декодировании используют таблицу синдромов (декодирования), представляющую собой список образцов ошибок (см. первый столбец стандартного расположения) и список соответствующих синдромов, которые однозначно характеризуют каждый смежный класс (см. раздел 4.1).
3. Коды Хэмминга
Кодом Хэмминга называется (n,k)-код, проверочная матрица которого имеет r = n-k строк и 2 r -1 столбцов, причем столбцами являются все различные ненулевые последовательности.
Пример. Для (7,4)-кода Хэмминга
или 
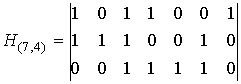
Проверочная матрица любого кода Хэмминга всегда содержит минимум три линейно зависимых столбца, поэтому кодовое расстояние кода равно трем.
Если столбцы проверочной матрицы представляют упорядоченную запись десятичных чисел, т.е. 1,2,3. в двоичной форме, то вычисленный синдром
однозначно указывает на номер позиции искаженного символа.
Пример. Для (7,4)-кода Хэмминга проверочная матрица в упорядоченном виде имеет вид
Пусть переданное кодовое слово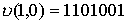 
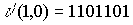
,а принятое слово — 
.
Синдром, соответствующий принятому слову будет равен
Вычисленный синдром указывает на ошибку в пятой позиции.
Проверочная матрица в упорядоченном виде представляет совокупность проверочных уравнений, в которых проверочные символы занимают позиции с номерами 2 i (i=0,1,2. ).
Для (7,4)-кода Хэмминга проверочными уравнениями будут
где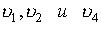 
— проверочные символы.
Элементы синдрома определяются из выражений
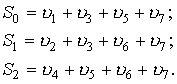
Корректирующая способность кода Хэмминга может быть увеличена введением дополнительной проверки на четность. В этом случае проверочная матрица для рассмотренного (7,4)-кода будет иметь вид
а кодовое расстояние кода d0=4.
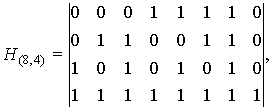
Проверочные уравнения используются для построения кодера, а синдромные — декодера кода Хэмминга.
Источник
