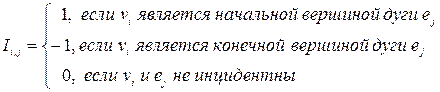Способы задания графов.
Рассмотрим три способа задания графов: графический, аналитический и матричный.
1) Графический способ.
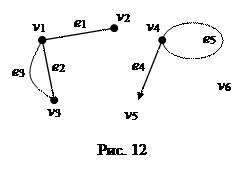
Вершины изображают точками на плоскости, а ребра – линиями, соединяющими соответствующие точки. Для изображения дуги используется линия со стрелкой, указывающей направление от начала к концу дуги.
На рисунке 12 изображен смешанный граф с вершинами v1, v2,¼, v6, ребрами e1, e2, e3, e5 и дугой e4. Смежные вершины v1, v2, инциденты ребру e1. Вершины v1, v3, инциденты параллельным ребрам e2 и e3. Вершине v4 инциденты петля e5 и дуга e4, причем v4 является началом дуги e4, а v5 – концом этой дуги. Степень вершины v1 равна 3, вершины v2 – 1, вершины v3 – 2, вершины v4 – 3, вершины v5 – 1, вершины v6 – 0. Таким образом, вершины v2 и v5 – висячие, а вершина v6 – изолированная. В случае дуги e4 точнее было бы говорить о полустепенях исхода и захода вершин v4 и v5, а именно: полустепень исхода вершины v4 равна 3, вершины v5 – 0, полустепень захода вершины v4 равна 2, вершины v5 – 1.
2) Аналитический способ.
3) Матричный способ.
Имеется несколько вариантов задать граф матрицей. Наиболее употребимыми являются матрица инциденций и матрица смежности.
а) Матрица инциденций – это прямоугольная матрица, число строк которой равно числу вершин, а число столбцов – числу дуг (ребер) графа. Элементы этой матрицы определяются следующим образом:
Таким образом, для графа на рисунке 12 матрица инциденций такова:
| e1 | e2 | e3 | e4 | e5 |
| v1 | ||||
| v2 | ||||
| I= | v3 | |||
| v4 | ||||
| v5 | -1 | |||
| v6 |
По этой матрице легко судить о наличии в графе параллельных ребер (два одинаковых столбца), петли (одна единица в столбце), дуги (значения разных знаков в столбце), изолированной вершины (нулевая строка), висячих вершин (одно ненулевое значение в строке).
б) Матрица смежности вершин – это квадратная матрица, размер которой определяется числом вершин в графе. Элементы этой матрицы определяются так: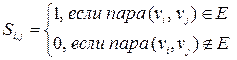 
. Если в графе имеются параллельные ребра, то соответствующий элемент матрицы смежности полагают равным числу этих ребер. Так матрица смежности для графа на рисунке 12 такова:
| v1 | v2 | v3 | v4 | v5 | v6 |
| v1 | |||||
| v2 | |||||
| S= | v3 | ||||
| v4 | |||||
| v5 | |||||
| v6 |
По виду этой матрицы также несложно судить о наличии в графе кратных ребер, дуг, петель, висячих и изолированных вершин.
Дата добавления: 2015-10-19 ; просмотров: 17444 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
MT1100: Дискретная математика
Помимо геометрического (графического) и аналитического способов задания графов существует еще, как минимум, три эквивалентых им способа.
Матрицей смежности для графа %%G = (V, E)%% называется квадратная матрица %%A = (a_
$$ A = \begin
Матрица смежности для примера из «Основных понятий»
Списком ребер графа называется таблица, состоящая из двух столбцов, в которой на пересечении %%i%%-й строки и первого (левого) столбца записывается ребро %%e_i%%, а на пересечении %%i%% -й строки и второго (правого) столбца записываются вершины, инцидентные ребру %%e_i%%.
Для того, чтобы список ребер однозначно задавал граф, необходимо помимо списка ребер указать множество всех изолированных вершин этого графа.
| 1 | %%B, C%% |
| 2 | %%A, C%% |
| 3 | %%B, F%% |
| 4 | %%A, F%% |
| 5 | %%A, F%% |
| 6 | %%A, D%% |
| 7 | %%D, F%% |
| 8 | %%D, E%% |
| 9 | %%E, F%% |
| 10 | %%B, E%% |
| 11 | %%E, E%% |
Список ребер для примера из «Основных понятий»
Матрицей инцидентности для графа %%G = (V, E)%% называется матрица %%B = (b_
Для неориентированного графа %%b_
У матрицы инцидентности есть пара особенностей:
- в каждой строке должны стоять две единицы, а все остальные символы — нули;
- она не используется для графов с петлями.
$$ B = \begin
Матрица инцидентности для примера из «Основных понятий» с учетом удаления петли у %%E%%
Источник
Понятие графа. Способы задания графа. Основные операции над графами. Основные типы графов.
Графом будем называть совокупность 2х конечных множеств вершин Х и ребер (или дуг) U
Если порядок соединения вершин (хi xj) является не существенным, то граф называется не ориентированным (неорграф), а пара (хi xj) — ребра этого графа. Если порядок соединения вершин (хi xj) является существенным, то граф называется ориентированным (орграф), а пара (хi xj) — дуги этого графа.. Граф, в котором имеются и дуги и ребра называется смешанным .Любое ребро не орграфа можно заменить парой дуг. Пара вершин графа (хi xj) может соединяться 2 я и более ребрами (дугами одного направления). Такие ребра (дуги) называются кратными. Количество одинаковых ребер (дуг) называется кратностью соответствующего ребра (дуги). Две вершины графа называются смежными, если существует соединяющее их ребро (дуга). 2 ребра называются смежными, если они имеют общею вершину. Петлей называются ребра, с совпадающей начальной и конечной вершиной. Граф с петлями и кратными дугами называется псевдограф, граф без петель и с кратными дугами называется мультиграф.
Подграфом графа G (х,u) называется граф G1(х1,u1), в котором множество x1 является подмножеством X, u1 является подмножеством u. Оставным подграфом графа G называется граф, содержащий все вершины графа G. Порожденный подграф состоит из подмножества вершин Xs множества вершин исходного графа и всех таких дуг графа G, у которого конечные и начальные вершины принадлежат подмножеству Xs .
Число дуг, исходящих из вершины xi ориентированного графа называется полустепенью исхода, число дуг, входящих в вершину ориентированного графа – полустепенью захода. В неор. Графах число ребер инцидентных вершине называется степенью вершины хi.
Вершина, имеющая степень 0 — изолированной., а имеющая степень 1 — висячей.
Маршрут —в не орграфе: последовательность ребер, в которой начало каждого последующего ребра совпадает с концом предыдущего. В орграфе: последовательность дуг, в которой начало каждой последующей дуги совпадает с концом предыдущей. Цепь —незамкнутый маршрут, в котором все ребра различны. Цепь, в которой все вершины различны, называется простой цепью. Путь — ориентированный маршрут, в котором все дуги различны. Замкнутый путь —контур. Цикл—замкнутая цепь. Замкнутая про стая цепь -простой цикл. Способы задания графа:
— геометрический (рисунок) – матричный. Различают также:
— матицу смежности (размерность пхп, щ = 1, если вершиныХ1И Xj смежны)
— матрицу инцидентности (размерность nxm, bjj = 1, если вершинахi инцидентна ребру Uj [для неорграфа] или b= 1, если вершина xi начальная вершина дуги uij bij = -1, если вершина xi., конечная вершина дуги и uij [для орграфа])
Основные операции над графами:
— удаление вершины (при этом удаляются все инцидентные ребра) — удаление ребра (при этом его конечные вершины не удаляются)
— добавление ре бра (обратно удалению) — слияние вершин – все ребра становятся инцидентны одной вершине
— стягивание ребра (удаление ребра и слияние его вершин) — подразбиение ребра (из графа удаляется (хi xj) и добавляется 2 новых ребра:(хi х0 и(х0 xj), где х0 — новая вершина)
Основные типы графов:
— орграф и неорграф
— граф с петлями и кратными ребрами называется псевдографом. Граф с кратными ребрами и без петель — мульти граф. Граф без петель и ребер- простой.
— граф называется взвешенным, если его ребрам (х^ xj) ставится в соответствие веса. Граф называется связным, если любые 2 вершины соединены маршрутом.
— граф называется ациклическим, если он не содержит циклов.
— орграф называется симметрическим, если любые 2 смежные вершины имеют пару противоположно направленных дуг. Неорграф -симметрический..
— граф называется регулярным степени к или однородным , если степени всех его вершин одинаковы и равны к.Число ребер при этом m=0.5*n*k.
— граф называется полным, если все его вершины смежные. К» —полный граф, содержащий п вершин.
— граф (X, U) называется двудольным, если множество его вершин X можно разделить на 2 подмножества Х1 Х2 таким образом, что каждое ребро графа имеет 1 конечную вершину в множестве X1, а другую —в Х2. Множества X1, Х2 — доли. Если любые 2 вершины графа из разных долей смежные, граф называется полным двудольным графом.
— граф называется эйлеровым, если он содержит эйлеров цикл —цикл, проходящий через каждое ребро графа 1 раз.
— граф называется гамипьтоновым, если он содержит гамипьтонов цикл — цикл, проходящий через каждую вершину 1 раз
— граф называется планарным, если его можно разложить на плоскости таким образом, чтобы ребра не пересекались в точке, отличной от вершины. Если он уже так расположен, то он назьшается плоским:
Укладок планерного графа на плоскости может быть несколько
— два графа G1, G2 изоморфны, если существует взаимно однозначное отображение между множествами их вершин, сохраняющее смежность. Для орграфа должна сохраняться ориентация дуг. Для псевдографов должна сохраняться кратность дуг. Изоморфные графы могут быть получены один из другого путем перенумерации вершин (пленарные и плоские графы).
125 Достижимость и связность в графе. Определение компонент связности в неорграфах и сильных компонент в орграфах.
В неорграфе и орграфе вершина Xj достижима из вершины хi если существует маршрут, соединяющий их (для орграфа- путь). Если в орграфе существует путь из хi вXj и обратно, то говорят, что эти вершины взаимно достижимые. Неорграф называется связным, если любые 2 вершины соединены маршрутом . Орграф называется сильно связным, если любые 2 вершины взаимно достижимы. Односторонне связным, если для любой пары хi Xj по крайней мере одна достижима из другой. Слабо связным, если можно указать 2 вершины, которые недостижимы ни в одну, ни в другую стороны, а не орграф, лежащий в основе данного орграфа, является связным.
Компоненты связности неорграфа называют его максимально связный подграф, т.е. подграф, не содержащийся ни в каком другом
связном подграфе этого графа. Сильные компоненты орграфа называют максимально сильный связный подграф.
Матрицей достижимости орграфа с n вершинами называется квадратная матрица R порядка n, элементы которой определяются
следующим образом 
, Xj достижима из xi(b противном случае, = О, ц= 1).
Матрицей контр достижимости орграфа с n вершинами называется квадратная матрица Q порядка n, элементы которой определяются: xi достижима из Xj (в противном случае, = 0, qj= 1).
МатрицыR, Q, S связаны: S=Q *R .Qтранспонированная матрица R
Матрицей сильной связности орграфа с п вершинами называется квадратная матрица S порядка п, элементы которой определяются
следующим образом Sij= 1, Хj xi— взаимно достижимы (в противном случае, = 0).
После определения матрицы S, по ней можно указать сильные компоненты графа: если Ху xi принадлежат одной сильной компоненте, то Sjj = 1, при этом строки (столбцы) соответствующие данным вершинам в матрице S одинаковы. Для не орграф а матрицы S, R, Qсовпадают.
Числом вершинной связности графа б (а) называется наименьшее число вершин, при удалении которых граф становиться не связным. Числом реберной связности графа а(а) называется наименьшее число ребер, при удалении которых граф становиться не связным. Вершина xi -точка сочленения, если при ее удалении связность графа нарушается. Ребро графа называется мостом, если его удаление приводит к нарушению связности.
127 Деревья. Построение деревьев с использованием поиска в глубину и в ширину. Алгоритмы Краскала и Прима построения кратчайшего остова графа.
Деревом называется связный ациклический граф. Ориентированным деревом называется орграф без циклов, в котором существует вершина x0, из которой имеется единственный путь в любую другую вершину графа. Деревом графа G называется его связный ациклический подграф. Остовым деревом графа называется дерево графа G, содержащее все вершины этого графа (остов T).
Ребра остового дерева называются ветвями, а ребра графа G, не принадлежащие остовому дереву, называются хордами. K – деревом называется ациклический граф, состоящий из k-компонентов связи.
Остов существует в любом графе, при чем он может быть определен не единственным способом.
Для остового дерева T справедливо:
— T – связный граф, но он утрачивает связность при удалении хотя бы одного ребра
— T – ациклический граф, но добавление к нему хотя бы одного ребра приводит к появлению цикла
— любые 2 вершины остовного дерева связаны единственной простой цепью
— остовое дерево содержит, по крайней мере, 2 висячие вершины
— число ребер остового дерева на единицу меньше числа его вершин.
Для построения остового дерева связного графа могут быть использованы 2 стратегии: поиск в глубину и поиск в ширину.
При поиске в глубину построение остова начинается с произвольной вершины графа x0. Затем выбирается вершина смежная с ней, например x1 и т.д. Если на k-ом шаге поиска для вершины xk существуют смежные вершины, которые не были еще просмотрены, происходит переход в одну из этих вершин, в противном случае, происходит возврат в предыдущею вершину xk-1 и поиск продолжается от нее. В процессе поиска вершины соединяются ребрами. Поиск заканчивается, когда будут просмотрены все вершины графа и произведен возврат в x0.
| 2 3 5 6 1 4 7 10 9 |
Поиск в ширину отличается от поиска в глубину тем, что на каждом шаге просматривается не одна, а все вершины смежные с текущей.
| 2 3 6 7 1 4 10 5 9 |
Кратчайшим остовом взвешенного графа называется остов, у которого сумма всех весов ребер наименьшая. Для построения кратчайшего остового дерева взвешенного графа могут быть использованы алгоритм Краскала или алгоритм Прима.
Алгоритм Краскала заключается в следующем: на начальном этапе из всех ребер графа G выбирается и включается в остов ребро U1, имеющее наименьший вес. На каждом последующем i-ом шаге из еще не включенных в остов ребер выбирается ребро, имеющее наименьший вес и не составляющее цикл с уже имеющимися ребрами. Процесс построения остового дерева завершается, когда в него будет включено n-1 ребро (n – количество вершин графа G).
Алгоритм Прима отличается от алгоритма Краскала тем, что в процессе построения необходимо следить за связностью строящегося дерева. При этом, если дерево Ti построено, то новое ребро выбирается не из всех оставшихся ребер графа, а только из тех, которые соединяют дерево Ti с вершинами, не включенными в него.
Источник
