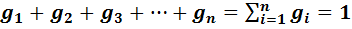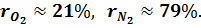Основные определения. Способы задания газовых смесей
В качестве рабочего тела тепловых двигателей и установок используется смесь различных газов, близких по своим свойствам к идеальным газам. Например, воздух представляет газовую смесь, состоящую из азота, кислорода, углекислого газа, водяных паров и одноатомных газов. Поэтому для решения практических задач необходимо уметь определять основные параметры газовой смеси.
Под газовой смесью понимается механическая смесь отдельных газов, не вступающих между собой ни в какие химические реакции. Каждый газ в смеси, независимо от других газов, полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объем смеси. Молекулы каждого газа смеси создают давление на стенки сосуда, которое называется парциальным (частичным).
Газовая смесь идеальных газов подчиняется закону Дальтона: общее давление смеси газов равно сумме парциальных давлений отдельных газов, составляющих смесь:
Р = Р1 +Р2 + . + Рn = 
Рi, (2.15)
где Рi— парциальные давления.
Парциальным давлением называют такое давление, которое имел бы каждый газ, входящий в состав смеси, если бы этот газ находился один в том же количестве, в том же объеме и при той же температуре, что и в смеси.
Параметры газовой смеси могут быть вычислены по уравнению Клапейрона PV = mRT, где все величины, входящие в уравнение, относятся к смеси газов.
Задачей расчета газовой смеси является определение на основании заданного состава смеси средней молярной массы или газовой постоянной смеси газов, после чего получение всех остальных параметров можно произвести по уравнению состояния для смеси.
Газовая смесь может быть задана массовыми, объемными и мольными долями.
Массовой долей называют отношение массы каждого газа к общей массе смеси:
где g1, . gn — массовые доли; m1, . mn — масса каждого газа;m— масса всей смеси.
Сумма всех массовых долей равна единице:
g1 + g2 + . + gn = gi = 1 (2.17)
Сумма масс всех газов равна массе смеси:
m1 + m2 + . + mn = mi = m.(2.18)
Объемной долей называют отношение парциального объема каждого газа к общему объему смеси газов:
где r1, . rn — объемные доли; V1, . Vn — парциальные объемы каждого газа;
V — объем смеси газов.
Парциальным объемом газа называют объем, который занимал бы этот газ, если бы его температура и давление равнялись температуре и давлению смеси газов. Парциальный объем каждого газа можно определить по закону Бойля-Мариотта. При постоянной температуре имеем:
Сложив правые и левые части этих выражений и учитывая закон Дальтона, получим:
V1 + V2 + . + Vn = Vi = V,(2.21)
т.е. сумма парциальных объемов газов, составляющих смесь, равна объему смеси газов.
Сумма объемных долей равна единице:
r1 + r2 + . + rn = ri = 1 (2.22)
Задание смеси мольными долями равнозначно заданию ее объемными долями. Действительно, если мольной долей назвать отношение числа киломолей каждого газа (Мi) к числу киломолей смеси газов (М), то учитывая, что
и 
(2.23)
Из закона Авогадро (r1/r2 = m1/m2 — плотности газов, находящихся при одинаковых температурах и давлениях, прямо пропорциональны их молярным массам) следует то, что при одинаковых Р и Т
. (2.24)
. (2.25)
Источник
Способы задания газовой смеси.
Массовая доля.
Наиболее простой способ определения состава газовой смеси – это определение массового состава смеси, т.е. для каждого газа находим его долю в общей массе смеси – массовую долю:
(18)
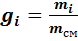
Очевидно, что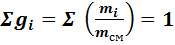 
,
т.е. 
Молярная доля.
Можно найти и молярный состав смеси. Действительно, зная молярные массы, находим количество вещества каждого компонента
(19)
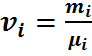
Следовательно, количество вещества в газовой смеси
(20)
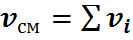
Имея эти данные, находим молярный состав смеси – молярные доли:
1)
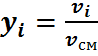
Молярную массу смеси можно определить следующим образом.
(22)
(23)
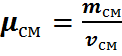
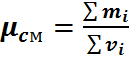
Полученное значение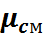 
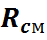
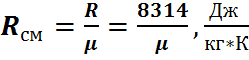
называется кажущейся, или условной, молярной массой смеси. Эта величина широко применяется в расчетах газовых смесей. Если известна (определена) молярная масса смеси, то можно найти удельную газовую постоянную смеси 
, используя уравнение (11), т.е.
(24)
Объёмная доля.
Наиболее часто задается объемный состав смеси, поэтому необходимо ввести понятие о парциальном объёме компонентов.
Пусть имеется газовая смесь из двух компонентов. Если собрать молекулы одного газа в одной части объёма, а молекулы другого газа в другой части. Части объёма каждого газа и называются парциальными. Подбирая соответствующим образом доли от общего объёма, можно добиться того, что каждый газ достигает давления смеси. Объёмы, которые занимают эти газы, называют приведенными, т.е. приведенными к давлению смеси. Сумма приведенных объемов равна объёму смеси (закон Амага):
(25)
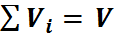
Отсюда может быть определен объёмный состав смеси, причем объёмная доля каждого компонента выражается отношением
(26)
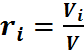
Так как каждый компонент смеси подвергается сжатию при постоянной температуре, то для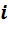 
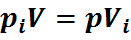
-го компонента смеси можно написать уравнение
, — это следует из закона Бойля – Мариотта. (27)
Здесь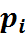 
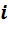
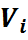
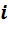
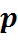
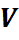
— парциальное давление — го компонента смеси газа;
— приведенный или парциальный объём — го компонента смеси газа;
— давление смеси газа;
— объём смеси газа.
Из уравнения (27) следует:
, (28)
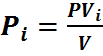
но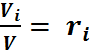 
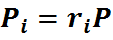
(26), тогда уравнение (28) запишем в виде:
(29)
Эта формула позволяет определять парциальные давления компонентов смеси, если известен объёмный состав смеси.
Так как при одинаковых давлениях и температурах молярные объёмы газов одинаковы, то можно написать для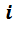 
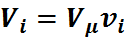
— го газа
, (30)
а для всей смеси
, (31)
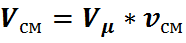
Из этих уравнений находим
, (32)
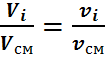
Следовательно, молярные доли численно равны объёмным:
(33)
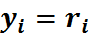
Связь между долями.
Массовые и объёмные (молярные) доли можно связать между собой, если известна плотность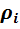 
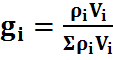
каждого компонента смеси. Тогда
(34)
(35)
Для определенной газовой смеси массовые и объёмные доли 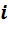– го компонента смеси будут различны, ввиду разной плотности компонентов смеси.
Из следствия 2 закона Авогадро известно, что плотности веществ зависят от их молярных (молекулярных) масс, т.е. они пропорциональны молярным массам.
Так, например, для сухого воздуха
в массовых долях,
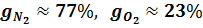
а в объёмных: 
Источник
Газовые смеси. Способы их задания. Закон Дальтона.
В практике чаще приходиться встречаться не с чистыми газами, а с их механическими смесями; одной из самых важных смесей является воздух, представляющий собой смесь азота и кислорода, с небольшой примесью аргона, углекислоты и водяного пара. Большое значение имеют такие газовые смеси, как природный газ (метан и другие углеводороды), продукты сгорания топлив (диоксид углерода, азот, водяной пар и т.п.).
Под газовой смесью понимается смесь отдельных газов, не вступающих между собой ни в какие химические реакции. Каждый газ (компонент) в смеси независимо от других газов полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объём смеси.
Для проведения расчетов с газовыми смесями необходимо установить параметры, характеризующие их состояние. Пусть имеется смесь из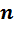 
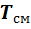
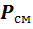
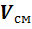
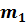
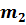
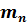
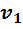
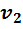
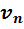
идеальных газов. Температура газовой смеси 
, давление её 
, объём 
; массы газов, находящихся в смеси, равны соответственно 
, 
. 
; количества веществ отдельных компонентов смеси 
, 
, …. , 
.
Если смесь находится в равновесии, то, несомненно, температура всех газов одинакова и равна температуре смеси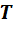 
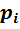
cм. В равновесном состоянии молекулы каждого газа рассеяны равномерно по всему объёму смеси, т.е. имеют свою определенную концентрацию и, следовательно, свое давление 
, называемое парциальным.
Парциальное давление – это давление, которое имел бы каждый газ, входящий в состав смеси, если бы этот газ находился один в том же количестве, в том же объёме и при той же температуре, что и в смеси.
Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси идеальных газов равно сумме парциальных давлений всех входящих в неё компонентов:
(16)
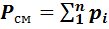
Этот закон был установлен Дальтоном в 1801 г.
Все зависимости, полученные для идеальных газов, справедливы и для их смесей, если в них подставить газовую постоянную (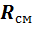 
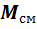
) и молекулярную (молярную) массу ( 
).
Очевидно, что масса газовой смеси равна сумме отдельных компонентов:
(17)
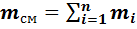
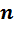
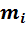
где : — число компонентов смеси;
— масса -го компонента.
Качественный состав газовой смеси может быть задан различными способами.
Источник
