Способы заданий функций принадлежности
При задании нечетких множеств наибольшую сложность представляет описание функций принадлежности. Существуют следующие способы заданий функций принадлежности:
1. Построение функций принадлежности альтернатив нечеткому множеству, соответствующему одному из возможных значений числовой лингвистической переменной, описывающей свойство альтернатив, на основе парных сравнений альтернатив по предпочтительности с точки зрения этого свойства. В этом случае при помощи языка бинарных отношений определяется степень выраженности данного свойства в каждой альтернативе. Степень принадлежности альтернативы нечеткому множеству, соответствующему одной из нечетких переменных, тем выше, чем с большим количеством других альтернатив данная альтернатива находится в отношении доминирования по данной нечеткой переменной.
2. Статистический подход, при котором значение функции принадлежности альтернативы нечеткому множеству, получается в результате обработки статистических данных, получаемых, например, при проведении многократно повторяющегося эксперимента. В качестве степени принадлежности альтернативы (числового значения базовой переменной) нечеткому множеству, соответствующему одному из возможных значений лингвистической переменной, описывающей свойство альтернативы, принимается оценка частоты использования этого значения лингвистической переменной при ее характеристике. Степень принадлежности альтернативы нечеткому множеству, соответствующему одной из нечетких переменных, тем выше, чем чаще данная нечеткая переменная является оценкой альтернативы в результате проведения эксперимента.
3. Экспертный подход, позволяющий построить функцию принадлежности по результатам выполнения процедуры экспертного оценивания. Степень принадлежности альтернативы нечеткому множеству, соответствующему одной из нечетких переменных, тем выше, чем больше результирующая оценка экспертами (меньше сумма рангов при ранжировании) альтернативы по данной нечеткой переменной.
4. Интервальное определение функций принадлежности, использующееся при решении задач выбора, в которых отсутствует четкая грань между допустимым и недопустимым, между идеальным и неудовлетворительным состоянием. Функция принадлежности альтернативы нечеткому множеству, соответствующему одному из возможных значений лингвистической переменной, описывающей свойство альтернативы, строится на основе уровневых ограничений идеальной области и недопустимой области значения оценки данного свойства по данной нечеткой переменной. Степень принадлежности альтернативы нечеткому множеству, соответствующему одной из нечетких переменных, тем выше, чем ее количественная оценка ближе к уровневому ограничению идеальной области для данной нечеткой переменной. Если количественная оценка альтернативы находится внутри идеальной области, то степень принадлежности альтернативы нечеткому множеству равна единице.
Дата добавления: 2018-06-28 ; просмотров: 690 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
2.2. Функции принадлежности и методы их построения
Введенное определение нечеткого множества (2.1) не накладывает ограничений на выбор функции принадлежности. Однако, на практике целесообразно использовать аналитическое представление функции принадлежности μ A x нечеткого множества A с элементами x , нечетко обладающими определяющим множество свойством R. Типизация функций принадлежности в контексте решаемой технической задачи существенно упрощает соответствующие аналитические и численные расчеты при применении методов теории нечетких множеств. Выделяют следующие типовые функции принадлежности [32] , [33] .
Треугольные функции принадлежности, использующиеся для задания неопределенностей типа: «приблизительно равно», «среднее значение», «расположен в интервале», «подобен объекту», «похож на предмет» и т.п.:
треугольная и трапецеидальная функции
Z-образные функции принадлежности, использующиеся для задания неопределенностей типа: «малое количество», «небольшое значение», «незначительная величина», «низкий уровень» и т.п.:
квадратичный и гармонический Z-сплайны
Z-сигмоидальная и Z-линейная функции
S-образные функции принадлежности, использующиеся для задания неопределенностей типа: «большое количество», «большое значение», «значительная величина», «высокий уровень» и т.п.:
квадратичный и гармонический S-сплайны
S-сигмоидальная и S-линейная функции
П-образные функции принадлежности, использующиеся для задания неопределенностей типа: «приблизительно в пределах от и до», «примерно равно», «около» и т.п.:
колоколообразная и гауссова функции
Существует множество других функций принадлежности нечетких множеств, заданных как композиции вышеупомянутых базовых функций (двойная гауссова, двойная сигмоидальная и т.п.), либо как комбинации по участкам возрастания и убывания (сигмоидально-гауссова, сплайн-треугольная и т.п.).
Функция принадлежности μ A x – это некоторая не вероятностная субъективная мера нечеткости, определяемая в результате опроса экспертов о степени соответствия элемента x понятию, формализуемому нечетким множеством A . В отличие от вероятностной меры, которая является оценкой стохастической неопределенности, имеющей дело с неоднозначностью наступления некоторого события в различные моменты времени, нечеткая мера является численной оценкой лингвистической неопределенности, связанной с неоднозначностью и расплывчатостью категорий человеческого мышления. При построении функции принадлежности μ A x с каждым нечетким множеством A ассоциируется некоторое свойство, признак или атрибут R , который характеризует некоторую совокупность объектов X . Чем в большей степени конкретный объект x ∈ X обладает этим свойством R , тем более близко к соответствующее значение μ A x . Если элемент x ∈ X определенно обладает этим свойством R , то μ A x = 1 , если же x ∈ X определенно не обладает этим свойством R , то μ A x = 0 . Существуют прямые и косвенные методы построения функций принадлежности [18] — [20] .
Прямые методы (наиболее известны методы относительных частот, параметрический, интервальный) целесообразно использовать для измеримых свойств, признаков и атрибутов, таких как скорость, время, температура, давление и т.п. При использовании прямых методов зачастую не требуется абсолютно точного поточечного задания μ A x . Как правило, бывает достаточно зафиксировать вид функции принадлежности и характерные точки, по которым дискретное представление функции принадлежности аппроксимируется непрерывным аналогом – наиболее подходящей типовой функцией принадлежности.
Косвенные методы (наиболее известен метод парных сравнений) используются в тех случаях, когда отсутствуют измеримые свойства объектов в рассматриваемой предметной области. В силу специфики рассматриваемых задач при построении нечетких систем автоматического управления, как правило, применяются прямые методы. В свою очередь, в зависимости от числа привлеченных к опросу экспертов как прямые, так и косвенные методы делятся на одиночные и групповые. Наиболее грубую оценку характеристических точек функции принадлежности можно получить путем опроса одного эксперта, который просто задает для каждого значения x ∈ X соответствующее значение μ A x .
Пример. Рассмотрим нечеткое множество A , соответствующее понятию «расход теплоносителя небольшой». Объект x – расход теплоносителя, X 0; x max – множество физически возможных значений скорости изменения температуры. Эксперту предъявляются различные значения расхода теплоносителя x и задается вопрос: с какой степенью уверенности 0 ≤ μ A x ≤ 1 эксперт считает, что данный расход теплоносителя x небольшой. При μ A x = 0 – эксперт абсолютно уверен, что расход теплоносителя x небольшой. При
Метод относительных частот. Пусть имеется m экспертов, n 1 из которых на вопрос о принадлежности элемента x ∈ X нечеткому множеству A отвечают положительно. Другая часть экспертов n 2 = m — n 1 отвечает на этот вопрос отрицательно. Тогда принимается
Пример. Рассмотрим нечеткое множество A , соответствующее понятию «скорость изменения температуры положительная средняя». Объект x – скорость изменения температуры, X — x max ; x max – множество физически возможных значений скорости изменения температуры. Экспертам предъявляются различные значения скорости изменения температуры x и каждому из них задается вопрос: считает ли эксперт, что данная скорость изменения температуры x положительная средняя. Результаты опроса сведены в табл.2.1.
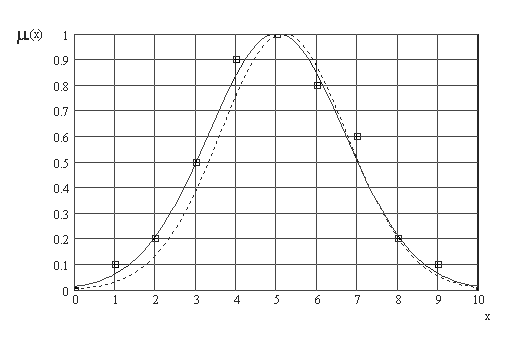
Для непрерывного представления нечеткой переменной используем какую нибудь из П-образных функций принадлежности, например, Гауссову. Из множества гауссовых функций gaussmf x,σ,c = exp — x — c 2 2 σ 2 через характерные точки функции принадлежности: точку перехода и максимум μ A 5 = 1 ; проходит функция с параметрами σ = 1,7 , c = 5 . В качестве альтернативного метода перехода от дискретного ряда точек к непрерывному заданию функции принадлежности можно предложить поиск параметров Гауссовой функции принадлежности, максимально близко аппроксимирующей дискретный ряд по критерию СКО (рис.2.4).
Рис.2.4. Аппроксимация дискретного ряда () непрерывной Гауссовой функцией принадлежности ( – по характерным точкам, – – по СКО)
Источник
Способы задания функций принадлежности
В работе [66] рассмотрены и исследованы различные способы получения функций принадлежности. Введена единая математическая форма представления различных способов определения функций принадлежности. Для описания нечетких множеств предложено применять сплайн-представление, в результате чего оказалось возможным выявить вклад того или иного источника информации в конечное решение.
Возможности построения многомерных функций принадлежности и аппроксимация их с помощью алгоритмов метода группового учета аргументов (МГУА) рассмотрены в работе [22] . В качестве примера для одного из УКПГ газового месторождения Медвежье построена функция принадлежности, зависящая от величины расхода и давления газа на УКПГ.
При использовании в качестве дополнительной переменной параметра времени t имеется возможность прогнозировать изменение функций принадлежности во времени и на их основе планировать ввод новых производственных мощностей и проведение различных ремонтных работ [134].
Разработаны также специальные преобразователи «аналог — функция принадлежности» [338], позволяющие получать функцию принадлежности непосредственно от датчика. Эти преобразователи удобно использовать в схемах коммутации, когда один сигнал вызывает несколько выходных в определенной последовательности, в логических схемах для обработки сильно зашумленных сигналов.
Предлагается также принцип аппаратурной реализации нескольких основных видов функций принадлежности, представляющих собой характеристику «вход — выход» элемента системы. Комбинированием элементов со специально подобранными функциями принадлежности можно стоить схемы со сложными нелинейными функциями [248].
В работе [314] для построения функций принадлежности на основе объективной информации и данных замеров предлагаются специальные блоки для выделения свойств (» property extractor «), например, с использованием детерминированного замера х * [314]
. (4.1)
В качестве 
берется установившееся (или среднее) значение параметра х, а величины 
и 
выбираются с учетом особенностей функции принадлежности и наилучших результатов по распознаванию сигналов (или управлению) в серии экспериментов [314].
Преимущества применения устройств, непосредственно построенных на элементах с многозначной логикой обсуждаются в работах [282, 284]. Отмечается перспективность использования многозначной логики для реализации регуляторов, устройств и систем с нечеткой логикой, которая может быть весьма полезной при создании систем принятия решений в условиях не полностью определенных данных.
В работе [336] предлагается реализация механизма нечеткого вывода на СБИС для возможности принятия решений при наличии неопределенных и приблизительных рассуждений. Проект устройства вывода основан на нечеткой арифметике и ориентирован на поддержку неопределенных знаний и способствует извлечению знаний человека-эксперта и имитации его процесса рассуждений. Быстродействие устройства около 80 тыс. ФЛИПС (нечетких логических выводов в секунду).
В Японии создан специальный Международный институт инженерных исследований по нечеткой логике ( Laboratory for international Fuzzy Engineering Research ). Основной задачей этого института является создание компьютера для приложений области нечеткой логики. Оцениваемый в 37 млн. долл. шестилетний бюджет института финансируется примерно 40 компаниями, среди которых Hitachi, Toshiba, Toyota.
В США налажено производство микропроцессора FC 110, предназначенного для программирования задач нечеткой логики во встроенных прикладных коммерческих системах реального времени. Производит эти микропроцессоры фирма TogaiInfraLogic Inc . Концептуальная методология нечеткой логики, предусматривающая количественное представление неточных значений в программируемых алгоритмах, оказалась весьма полезной при решении задач искусственного интеллекта в реальном времени.
В задачах математического программирования параметры задач зависят от многих факторов, которые сложно учесть в модели [179] . Внесение этих зависимостей в модель значительно ее усложняет и повышает размерность задачи, а «уточнение модели таким путем на практике сведется на нет из-за невозможности измерить или измерить с достаточной точностью величины введенных в модель факторов» [179] . То есть, для параметров моделей более естественным было бы задание интервала возможных значений или функции принадлежности.
Вопросы приближения функций принадлежности и нечетких отношений и выбора среди функций принадлежности, согласованных с заданным отношением, такой, которая наилучшим образом приближает предъявленную, рассмотрены в [106].
Большая часть работ по проблеме построения F -функций связана с методами обработки экспертных данных и результатов опроса специалистов [65, 98, 99, 318]. Метод позволяет включить в состав ограничений на систему некоторые субъективные ограничения, которые могут быть вызваны тем, что человек обладает рядом неформальных сведений о системе на естественном языке.
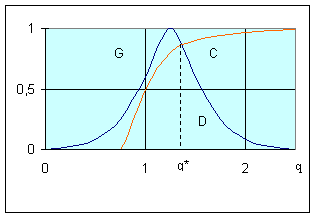
Например, цель G вида «дебит скважины должен быть близок к 1,2 млн.м куб./сут» или ограничение С «дебит должен быть больше 0,8 млн.м куб./сут» могут быть представлены соответственно следующим образом:
; (4.2)
; (4.3)
В общем случае эти лингвистические ограничения могут быть представлены в виде 
(рис.4.1).
Таким образом, характер функции зависит от трех параметров [289]: с — определяет точку максимума функции принадлежности 
для b>0 или минимума 
для b 0; а — размах кривой; b — поведение фронтов кривой.
В теории нечетких множеств отсутствуют различия между целями и ограничениями, заданными на множестве альтернатив Х, так как и цели, и ограничения представляются в виде функций принадлежности.
Для приведенного выше примера (4.2) — (4.3) нечеткое решение D с учетом цели G и ограничения С может быть представлено функцией принадлежности (рис.4.2)
(4.4)
В качестве четкого решения по дебиту скважины может быть принято решение q *=1,36 млн.м 3 /сут., при котором функция принадлежности для нечеткого решения достигает максимального значения (рис.2.5).
Рис.4.2.Нечеткое решение по выбору дебита скважины с учетом нечетких цели G и ограничения С.
С помощью функции принадлежности можно адекватно отразить мнение одного или нескольких экспертов. Это связано с неспособностью человека формулировать свое количественное впечатление в виде одиночного числа [179].
Пусть эксперт в качестве оптимального дебита скважины называет дебит 1,5 млн.м куб./сут. Но это не значит, что величины незначительно отличающиеся от него будут совершенно неприемлемыми, т.е. степени принадлежности 
и 
будут незначительно отличаться от 
. Результат экспертного опроса может задаваться в виде таблицы или непрерывной функции.
Пусть имеется m экспертов, часть которых на вопрос о принадлежности элемента x 
X нечеткому множеству A отвечает положительно. Обозначим их число через n1 . Другая часть экспертов n2=m-n1 отвечает на этот вопрос отрицательно. Тогда принимается, что
Пример 4.1. Пусть имеется множество X= и требуется построить нечеткое множество A , формализующее нечеткое понятие “намного больше двух”. Допустим, что результаты опроса шести экспертов показаны в табл.4.2:
Источник
