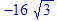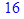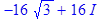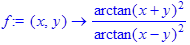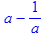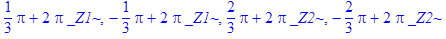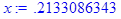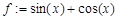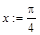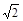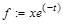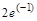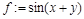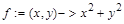СКА Maple. Способы задания функций.
Способ 1. Определение функции с помощью оператора присваивания (:=): какому-то выражению присваивается имя, например: > f:=sin(x)+cos(x); Способ 2. Определение функции с помощью функционального оператора, который ставит в соответствие набору переменных (x1,x2,…) одно или несколько выражений (f1,f2,…). Например, определение функции двух переменных с помощью функционального оператора выглядит следующим образом: > f:=(x,y)->sin(x+y); Способ 3. С помощью команды unapply(expr,x1,x2,…), где expr – выражение, x1,x2,… – набор переменных, от которых оно зависит, можно преобразовать выражение expr в функциональный оператор. Например:
> f:=unapply(x^2+y^2,x,y);
СКА Maple. Аналитическое решение уравнений.
Для решения уравнений в Maple существует универсальная команда solve(eq,x), где eq – уравнение, x – переменная, относительно которой уравнение надо разрешить. В результате выполнения этой команды в строке вывода появится выражение, которое является решением данного уравнения. Например: > solve(a*x+b=c,x); Если уравнение имеет несколько решений, которые вам понадобятся для дальнейших расчетов, то команде solve следует присвоить какое-нибудь имя name. Обращение к какому-либо k–ому решению данного уравнения производится указанием его имени с номером решения k в квадратных скобках: name[k]. Например: > x:=solve(x^2-a=0,x);
СКА Maple. Численное решение уравнений.
Для численного решения уравнений, в тех случаях, когда трансцендентные уравнения не имеют аналитических решений, используется специальная команда fsolve(eq,x), параметры которой такие же, как и команды solve. Например: > x:=fsolve(cos(x)=x,x);
СКА Maple. Решение неравенств.
Команда solve применяется также для решения неравенств. Решение неравенства выдается в виде интервала изменения искомой переменной. В том случае, если решение неравенства полуось, то в поле вывода появляется конструкция вида RealRange(– , Open(a)), которая означает, что x (– , a), а – некоторое число. Слово Open означает, что интервал с открытой границей. Если этого слова нет, то соответствующая граница интервала включена во множество решений. Например: > s:=solve(sqrt(x+3) convert(s,radical); Если вы хотите получить решение неравенства не в виде интервального множества типа x (a, b), а в виде ограничений для искомой переменной типа a solve(1-1/2*ln(x)>2,
СКА Maple. Двухмерная графика.
Команда plot и ее параметры.
Для построения графиков функции f(x)одной переменной (в интервале 
по оси Ох и в интервале 
по оси Оу) используется команда plot(f(x), x=a..b, y=c..d, parameters),гдеparameters– параметры управления изображением. Если их не указывать, то будут использованы установки по умолчанию. Настройка изображения также может осуществляться с панели инструментов.
Основные параметры команды plot:
1) title=”text”,гдеtext-заголовок рисунка ; 2) coords=polar –установка полярных координат ;3) axes– установка типа координатных осей; 4) scaling – установка масштаба рисунка; 5) style=LINE(POINT) – вывод линиями (или точками); 6) сolor– установка цвета линии: английское название цвета, например,yellow– желтый и т.д. 7) font=[f,style,size]– установка типа шрифта для вывода. С помощью команды plot можно строить помимо графиков функций y=f(x), заданной явно, также графики функций, заданных параметрически y=y(t), x=x(t), если записать команду plot([y=y(t), x=x(t), t=a..b], parameters).
Дата добавления: 2018-04-15 ; просмотров: 288 ; Мы поможем в написании вашей работы!
Источник
Основы Maple
Функции и выражения
Функции или функциональные выражения вида f(x) или expr(args) – это вызов функции или применение функции (или процедуры) к аргументам args.
Для анализа типа функций каждого узла и ветви применяют команды whattype , nops , op .
Активные функции (начинаются с маленькой буквы) применяются для расчетов, например, diff , int , limit (об активных/инертных формах функций пакета Physics – см. описание команд пакета).
Инертные функции (начинаются с большой буквы) применяются для показа шагов при решении задачи, например, Diff , Int , Limit .
Два класса функций: библиотечные (заранее опредленные) и функции пользователя. Подробнее – см. в главе Правила формального синтаксиса команд Maple разделы Функции пользователя и далее. Там же приведены сведения о синтаксисе процедур и модулей, объектов и операций, управляющих структур, основных операций со структурами данных.
Выражение expr: действующий оператор, сформированный из комбинации команд, констант, переменных, функций.
Внешне эту запись можно перепутать с вызовом функции.
Отличие от вызова функции в том, что именно следует сделать, чтобы вычислить определенное значение x :
Пишeте (вызываете) Fn1(x) – и ничего не получается!
Вместо этого надо было присвоить x значение:
затем вычислить Fn1 :
Функция Maple определяется так:
Эта конструкция ведет себя как функция: ей дается аргумент, а она возвращает ответ:
Можно определить функцию многих аргументов:
Следовательно, знак -> обозначает функцию, как принято в математике. (Формальный синтаксис и более подробные сведения – см. Функции пользователя.)
Так зачем же вводить понятие выражения, которое запутывает ситуацию? Потому что зачастую Maple проще (и быстрее) работает с выражением: алгебраическими преобразованиями, дифференцированием, интегрированием, решением ДУ, построениием графиков. К этому надо привыкнуть. Разницу между выражением и функцией можно понимать так:
Выражение Maple подобно функции в книге по математике, а функция Maple подобна устройству, которое имеет вход и выход.
Если функция слишком сложна, чтобы быть записанной с помощью оператора – стрелки, то применяются Процедуры и модули (там же).
Источник
Функции в Maple. Операции оценивания. Решение уравнений и неравенств
Контрольные задания
1. Дано комплексное число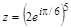 
. Найти его вещественную и мнимую части, модуль и аргумент.
> restart;
> z:=(2*exp(I*Pi/6))^5:
> evalc(Re(z)); evalc(Im(z));
> evalc(readlib(polar)): evalc(polar(z));
2. Записать функцию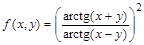 
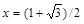
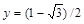
в виде функционального оператора и вычислите ее значения при x=1, y=0 и при 
, 
.
> restart;
> f:=(x,y)->(arctan(x+y)/arctan(x-y))^2;
> f(1,0);
> f((1+sqrt(3))/2,(1-sqrt(3))/2);
3. Записать функцию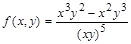 
с помощью оператора присваивания и вычислите ее значение при x=a, y=1/a, используя команду подстановки subs.
> restart;
4. Найти все точные решения системы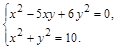 
в аналитическом виде.
> restart;
5. Найти все решения тригонометрического уравнения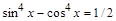 
.
> restart;
> _EnvAllSolutions:=true:
> solve(sin(x)^4-cos(x)^4=1/2, x);
6. Найти численное решение уравнения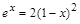 
.
> restart;
> x:=fsolve(exp(x)=2*(1-x)^2, x);
7. Решить неравенство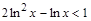 
.
> restart;
> s:=solve(2*ln(x)^2-ln(x) f:=sin(x)+cos(x);
Если задать конкретное значение переменной х, то получится значение функции f для этого х. Например, если продолжить предыдущий пример и вычислить значение f при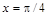 
, то следует записать:
После выполнения этих команд переменная х имеет заданное значение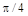 
.
Чтобы насовсем не присваивать переменной конкретного значения, удобнее использовать команду подстановки subs(
Способ 2. Определение функции с помощью функционального оператора, который ставит в соответствие набору переменных (x1,x2,…) одно или несколько выражений (f1,f2,…). Например, определение функции двух переменных с помощью функционального оператора выглядит следующим образом:
Обращение к этой функции осуществляется наиболее привычным в математике способом, когда в скобках вместо аргументов функции указываются конкретные значения переменных. В продолжение предыдущего примера вычисляется значение функции:
Способ 3. С помощью команды unapply(expr,x1,x2,…), где expr – выражение, x1,x2,… – набор переменных, от которых оно зависит, можно преобразовать выражение expr в функциональный оператор. Например:
Какие операции оценивания производятся в Maple с действительными выражениями?
В Maple имеются следующие команды оценивания действительных выражений:
frac(expr) — вычисление дробной части выражения expr;
trunc(expr) — вычисление целой части выражения expr;
round(expr) — округление выражения expr;
Для чего предназначена команда evalf?
Все вычисления в Maple по умолчанию производятся символьно, то есть результат будет содержать в явном виде иррациональные константы, такие как, и другие. Чтобы получить приближенное значение в виде числа с плавающей запятой, следует использовать команду evalf(expr,t), где expr — выражение, t — точность, выраженная в числах после запятой.
С помощью каких команд можно найти вещественную и мнимую части комплексного выражения, а также его модуль и аргумент, и комплексно сопряженное ему число? Какую роль выполняет команда evalc?
Вещественную и мнимую части комплексного выражения z=x+iy можно найти с помощью команд Re(z) и Im(z). Например:
Если z=x+iy, то комплексно сопряженное ему выражение w=z*=x-iy можно найти с помощью команды conjugate(z). Продолжение предыдущего примера:
Модуль и аргумент комплексного выражения z можно найти с помощью команды polar(z), которую необходимо предварительно вызвать из стандартной библиотеки командой readlib. Например:
Если комплексное выражение очень сложное или содержит параметры, то команды Re(z) и Im(z) не дают требуемого результата. Получить вещественную и мнимую части комплексного выражения z можно, если использовать команду преобразования комплексных выражений evalc(z). (> evalc(Re(z)); evalc(Im(z));)
Источник
