- Функции и способы задания функций
- Определение функции
- Готовые работы на аналогичную тему
- Аналитический способ задания функции
- Табличный способ задания функции
- Графический способ задания функции
- Пример задачи
- Понятие функции. Способы задания функции
- Классификация функций.
- Определение функции. Способы задания функции.
- Способы задания функции.
- Аналитический способ задания функции.
- Графический способ задания функции.
- Табличный способ задания функции.
Функции и способы задания функций
Вы будете перенаправлены на Автор24
Определение функции
Существуют множество определений для понятия «функция».
Одними из классических определений понятия «функция» считаются определения на базе соответствий. Приведем ряд таких определений.
Зависимость, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называется функцией.
Пусть даны два непустых множества $X$ и $Y$. Соответствие $f$, которое каждому $x\in X$ сопоставляет один и только один $y\in Y$ Называется функцией ($f:X → Y$).
Пусть $M$ и $N$ — два произвольных числовых множества. Говорят, что на $M$ определена функция $f$, принимающая значения из $N$, если каждому элементу $x\in X$ поставлен в соответствие один и только один элемент из $N$.
Следующее определение дается через понятие переменной величины. Переменной величиной называется величина, которая в данном исследовании принимает различные числовые значения.
Пусть $M$ — множество значений переменной величины $x$. Тогда, сели каждому значению $x\in M$ соответствует одно определенное значение другой переменной величины $y$ есть функция величины $x$, определенной на множестве $M$.
Далее рассмотрим теоретико-множественные определения.
Пусть $X$ и $Y$ — некоторые числовые множества. Функцией называется множество $f$ упорядоченных пар чисел $(x,\ y)$ таких, что $x\in X$, $y\in Y$ и каждое $x$ входит в одну и только одну пару этого множества, а каждое $y$ входит, по крайней мере, в одну пару [15].
Всякое множество $f=\<\left(x,\ y\right)\>$ упорядоченных пар $\left(x,\ y\right)$ таких, что для любых пар $\left(x’,\ y’\right)\in f$ и $\left(x»,\ y»\right)\in f$ из условия $y’≠ y»$ следует, что $x’≠x»$ называется функцией или отображением [7].
Готовые работы на аналогичную тему
Функция $f:X → Y$ — это множество $f$ упорядоченных пар $\left(x,\ y\right)\in X\times Y$, таких, что для любого элемента $x\in X$ существует единственный элемент $y\in Y$ такой, что $\left(x,\ y\right)\in f$, то есть функция — кортеж объектов $\left(f,\ X,\ Y\right)$.
В этих определениях
$x$ — независимая переменная.
$y$ — зависимая переменная.
Все возможные значения переменной $x$ называется областью определения функции, а все возможные значения переменной $y$ называется областью значения функции.
Далее будем рассматривать три способа для задания функций: аналитический, табличный и графический.
Аналитический способ задания функции
Для этого способа нам понадобится понятие аналитического выражения.
Аналитическим выражением называется произведение всех возможных математических операций над какими-либо числами и переменными.
Аналитическим способом задания функции и является её задание с помощью аналитического выражения.
Приведем далее преимущества и недостатки данного способа:
Плюсы:
- С помощью формул мы можем определить значение функции для любого определенного значения переменной $x$;
- Функции, заданные таким способом можно изучать с помощью аппарата математического анализа.
Минусы:
- Малая наглядность.
- Иногда приходится производить очень громоздкие вычисления.
Табличный способ задания функции
Данный способ задания состоит в том, что для нескольких значений независимой переменной выписываются значения зависимой переменной. Все это вносится в таблицу.
Плюс: Для любого значения независимой переменной $x$, которая внесена в таблицу, сразу узнается соответствующее значение функции $y$.
Минусы:
- Чаще всего, нет полного задания функции;
- Малая наглядность.
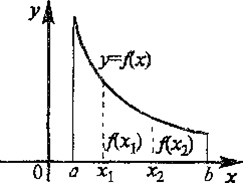
Графический способ задания функции
Введем понятие графика функции:
Графиком функции $f(x)$ называется множество точек координатной плоскости, которые имеют вид $(x,\ f\left(x\right))$.
Задание графика с помощью такого изображения его в декартовой системе координат называется графическим способом.
Пример задачи
Дан аналитический вид функции $y=x^2$. Привести табличный и графический способы задания этой же функции.
Решение.
Сначала приведем табличный способ. Так как при возведении в четную степень любого числа получим неотрицательное значение, то получим следующую таблицу:
Это и есть табличное задание.
Перейдем теперь к заданию в виде графика. Для этого отметим в декартовой системе координат точки из таблицы выше. Получим:
Источник
Понятие функции. Способы задания функции



Понятие функции является одним из основных понятий современной математики. С этим понятием часто встречаются при изучении реальных процессов в природе, науке и технике. С помощью различных функций могут быть описаны многие процессы и явления реального мира.
Определение. Отображения 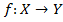
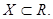
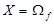
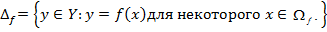
Определение. Если каждому элементу х множества X ( 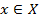
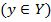
y = f(x), y = F(x) — функциональная зависимость х и у.
f, F — характеристики функции, х — независимая переменная (аргумент),
у — зависимая переменная.
Рассматривают три способа задания функции: аналитический, табличный и графический.
Способ задания функции при помощи формулы называется аналитическим.Этот способ является основным в мат. анализе, но на практике не удобен.
2. Табличный способ задания функции .
Функцию можно задать с помощью таблицы, содержащей значения аргумента и соответствующие им значения функции.
3. Графический способ задания функции .
Функция у = f(х) называется заданной графически, если построен ее график. Такой способ задания функции дает возможность определять значения функции только приближенно, так как построение графика и нахождение на нем значений функции сопряжено с погрешностями
Классификация функций.
Элементарные функции разделяют на алгебраические и неалгебраические (трансцендентные).
Алгебраической называют функцию, в которой над аргументом производится конечное число алгебраических действий.
К ним относятся:
— целая рациональная функция (многочлен, полином)
— дробно-рациональная функция – отношение двух многочленов
— иррациональная функция (среди действий над аргументом есть извлечение корня).
К трансцендентным относятся: показательная, логарифмическая, тригонометрические и обратные тригонометрические функции.
Четные и нечетные функции.
Функция у = f(х) называется четной или нечетной, если она определена на множестве симметричном относительно нулевой точки и обладает на нем свойством f(-x)=f(x) или свойством f(-x) = -f(x). В противном случае функцией общего вида. График четной функции симметричен относительно оси ординат, график нечетной симметричен относительно начала координат.
Произведения двух четных или двух нечетных функций есть функция четная, произведения четной функции на нечетную есть нечетная функция
Монотонные функции.
Пусть (a,b) промежуток с концами в точках a и b, где a
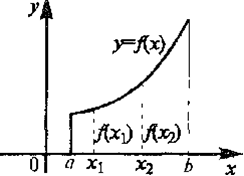
Функция у = f(х) называется возрастающей (убывающей) на промежутке (a,b), если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть 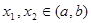
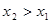
Тогда функция возрастает на промежутке X, если 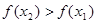
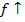
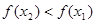
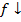
Запись 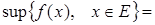
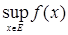
Функции возрастающие и убывающие называется монотонными. К монотонным функциям относятся также неубывающие и невозрастающие функции.
Ограниченные функции.
Функция называется ограниченной на промежутке (a,b), если 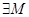
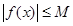
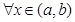
В противном случае функция называется неограниченной.
Периодическая функция.
Функция называется периодической с периодом 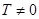
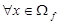
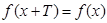
Источник
Определение функции. Способы задания функции.
Что значить задать функцию? Какими способами можно задать функцию? Что такое определение функции?
Задать функцию — это значит указать правило, при задании любого значения аргумента x вы найдете значение функции y.
Функция y=f(x) – зависимость переменной y от переменной x. Когда задаем значение аргумента x, получаем единственное значение функции y.
Способы задания функции.
В данной статье рассмотрим 3 способа задания функции. На самом деле их больше, в школьной программе чаще всего разбирают эти способы задания функции.
Аналитический способ задания функции.
Чаще всего в школьной программе правило задают в виде формулы y=f(x), x∈X или нескольких формул. Такой способ задания функции называется аналитическим.
Примеры аналитического задания функции:
Графический способ задания функции.
Также если по формуле построить график функции, то данный способ задания функции будет называться графическим. Не всегда вам будут давать график совместно с формулой. Иногда вам в заданиях будут давать только график функции, по которому вы должны будете найти определенные данные. По графику функции можно восстановить его формулу, но это не всегда легко сделать, все зависит от начерченного графика. В школьной программе вам будут задавать графики, по которым вы сможете рассчитать формулу.
Примеры, графического задания функции:


 Табличный способ задания функции.
Табличный способ задания функции.
Следующий способ задания функции применяется чаще всего на практике называется табличный.
Все данные представлены в виде таблице. У этого способа имеется конечное множество значений аргумента. Такими таблицами вы уже пользовались в алгебре, например, таблица квадратов, таблица корней и т.д.
Примеры, табличного задания функции:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
Рассмотрим примеры по теме «Способы задания функции»:
Пример №1:
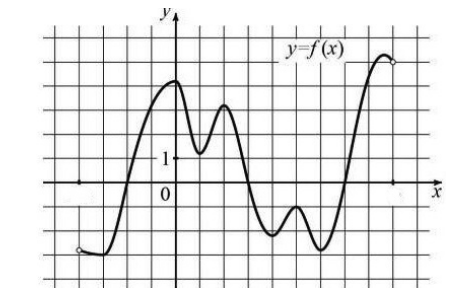
Является ли графическим заданием какой-либо функции фигура?


Является ли графическим заданием какой-либо функции фигура?
Сколько бы мы не проводили вертикальных линий, всегда будет одно пересечение с графиком. Следовательно, изображенная фигура является графиком функции.

Является ли графическим заданием какой-либо функции фигура?

Источник






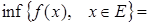
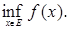


 Табличный способ задания функции.
Табличный способ задания функции.



