Способы задания функции 7 класс алгебра определение

Дидактические материалы для занятий математического кружка «Математика +» 7 класс. Занятие21. Понятие функции. Способы задания функции
план-конспект занятия по математике (7 класс) на тему

Математический кружок- одна из наиболее эффективных форм внеклассных занятий. Для меня, как учителя, важно иметь под рукой пособие, в котором представлены идеи решений и которое позволило бы провести цикл занятий математического кружка не прилагая титанических усилий для подбора материала. Мной предпринята попытка составления такой разработки, которую можно было использовать при подготовке к занятиям.

Скачать:

Вложение	Размер
zanyatie_21._ponyaie_funktsii._sposoby_zadaniya_funktsii.docx	95.49 КБ

Предварительный просмотр:

Понятие функции одной переменной

Рассмотрим два числовых множества X и Y . Правило f , по которому каждому числу х ∈ Х ставится в соответствие единственное число y ∈ Y , называется числовой функцией , заданной на множестве Х и принимающей значения во множестве Y .

Таким образом, задать функцию, значит задать три объекта:

1) множество Х (область определения функции);

2) множество Y (область значений функции);

3) правило соответствия f (сама функция).

Например, поставим в соответствие каждому числу его куб. Математически это можно записать формулой y=x 3 . В этом случае правило f есть возведение числа х в третью степень. В общем случае, если каждому х по правилу f соответствует единственный y , пишут y = f(x). Здесь » х » называют независимой переменной или аргументом , а » y » — зависимой переменной (т.к. выражение типа x 3 само по себе не имеет определенного числового значения пока не указано значение х ) или функцией от х . О величинах х и y говорят, что они связаны функциональной зависимостью. Зная все значения х и правило f можно найти все значения у . Например, если х=2 , то функция f(x) =x 3 принимает значение у = f(2) =2 3 =8 .

Подведем итог:

Зависимость одной переменной от другой называется функциональной зависимостью. Зависимость переменной y от переменной x называется функцией , если каждому значению x соответствует единственное значение y .

Переменную x называют независимой переменной или аргументом , а переменную y — зависимой. Говорят, что y является функцией от x . Значение y , соответствующее заданному значению x , называют значением функции .

Все значения, которые принимает x , образуют область определения функции ; все значения, которые принимает y , образуют множество значений функции .

D(f) — значения аргумента. E(f) — значения функции. Если функция задана формулой, то считают, что область определения состоит из всех значений переменной, при которых эта формула имеет смысл.

Графиком функции называется множество всех точек на координатной плоскости , абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. Если некоторому значению x=x 0 соответствуют несколько значений (а не одно) y , то такое соответствие не является функцией. Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая параллельная оси Оу, пересекалась с графиком не более чем в одной точке.

Способы задания функции одной переменной

Существуют несколько способов задания функции.

Аналитический способ. Функция f задается в виде формулы y=f(x). Этот способ является преобладающим в математических исследованиях и подробно рассматривается в классическом курсе математики. Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например y=3x+2x 2 . Здесь значению x = 1 соответствует y=3∙1+2∙1 2 =5 , значению x=2 соответствует y=3∙2+2∙2 2 =6+8=14 и т. д.

Функция может быть задана на разных частях множества X разными функциями. Например:

Чем хорош аналитический способ задания функции? Тем, что если у вас есть формула — вы знаете про функцию всё! Вы можете составить табличку. Построить график. Исследовать эту функцию по полной программе. Точно предсказать, где и как будет вести себя эта функция. Но в исследованиях соответствие между переменными величинами x и y не всегда удается записать в виде формулы. Во многих случаях формула бывает неизвестна. Тогда для выражения функциональной зависимости используются другие способы.

Табличный способ . Этот способ является наиболее простым. В одной строке таблицы записываются все значения аргумента (числа), а в другой – значения f(x) , соответствующие каждому х . Например, зависимость температуры воздуха (Т) от времени суток (t) в определенный день можно представить таблицей.

Источник

Понятие функции

Урок 12. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Понятие функции»

· ввести понятия «функциональная зависимость»;

· узнать о способах задания функции;

· познакомиться с историей функции.

Изучение темы начнём с рассмотрения нескольких примеров.

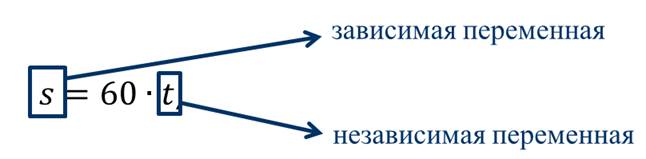
В рассмотренном примере переменную t называют независимой переменной, так как её значения мы выбирали произвольно. А переменную s называют зависимой переменной, так как её значения определяются выбранными значениями переменной t.

Давайте рассмотрим ещё один пример.

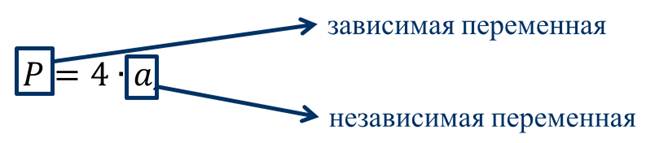
В этом примере переменная а является независимой переменной, а переменная Р – зависимой переменной.

В рассмотренных примерах каждому значению независимой переменной соответствует единственное значение зависимой переменной. Такую зависимость одной переменной от другой называю функциональной зависимостью или функцией.

Независимую переменную называют также аргументом, а зависимую – функцией от этого аргумента.

Так в рассмотренных примерах путь, пройденный автомобилем, является функцией от времени движения автомобиля. А периметр квадрата является функцией от его стороны.

Значения, которые принимает независимая переменная, образуют область определения функции.

Все значения зависимой переменной называют значениями функции.

А сейчас выполним следующее упражнение.

В семнадцатом веке французские математики Рене Декарт и Пьер Ферма впервые начали выражать зависимость между переменными при помощи формулы.

В рассмотренных выше примерах функции задавались с помощью формулы. И этот способ задания функции является более распространённым. Но давайте рассмотрим ещё несколько примеров.

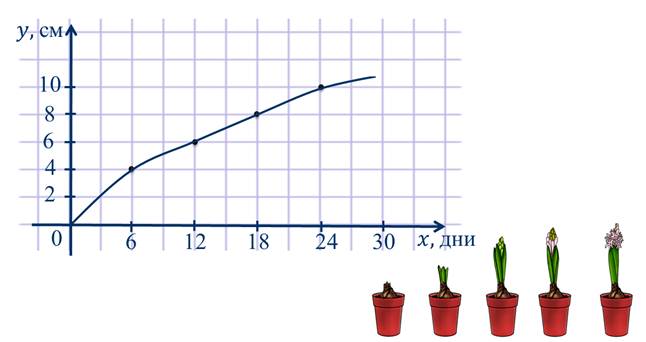
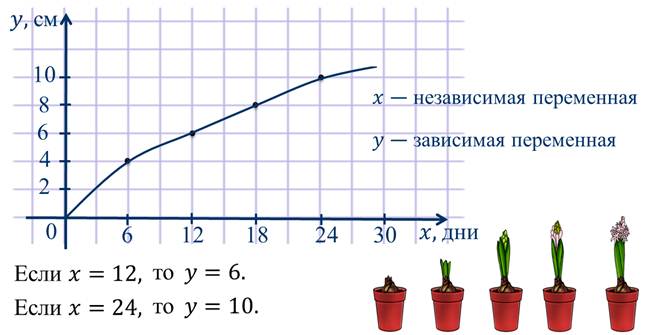
На рисунке показано, как изменялась высота гиацинта в зависимости от его возраста. Рост указан в сантиметрах, а его возраст в днях.

С помощью этого графика мы можем сказать, какую высоту имеет цветок в зависимости от его возраста. Например,

В данном случае икс является независимой переменной, а игрек – зависимой переменной.

Здесь зависимость одной переменной от другой также является функциональной зависимостью, или функцией. Но, в отличие от предыдущих примеров, функция задана в виде графика.

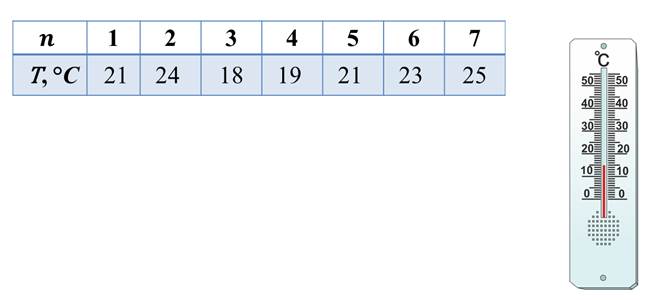
И рассмотрим таблицу, в которой представлен результат измерений средней температуры воздуха в комнате в течение недели.

В данной таблице каждому значению n (то есть номеру дня недели) соответствует значение t (температуры воздуха в комнате). Например,

Здесь каждому значению независимой переменной соответствует единственное значение зависимой переменной.

А такую зависимость мы называем функцией. В этом примере функция задана в виде таблицы.

Источник

Определение функции. Способы задания функции.

Что значить задать функцию? Какими способами можно задать функцию? Что такое определение функции?

Задать функцию — это значит указать правило, при задании любого значения аргумента x вы найдете значение функции y.

Функция y=f(x) – зависимость переменной y от переменной x. Когда задаем значение аргумента x, получаем единственное значение функции y.

Способы задания функции.

В данной статье рассмотрим 3 способа задания функции. На самом деле их больше, в школьной программе чаще всего разбирают эти способы задания функции.

Аналитический способ задания функции.

Чаще всего в школьной программе правило задают в виде формулы y=f(x), x∈X или нескольких формул. Такой способ задания функции называется аналитическим.

Примеры аналитического задания функции:

Графический способ задания функции.

Также если по формуле построить график функции, то данный способ задания функции будет называться графическим. Не всегда вам будут давать график совместно с формулой. Иногда вам в заданиях будут давать только график функции, по которому вы должны будете найти определенные данные. По графику функции можно восстановить его формулу, но это не всегда легко сделать, все зависит от начерченного графика. В школьной программе вам будут задавать графики, по которым вы сможете рассчитать формулу.

Примеры, графического задания функции:

Табличный способ задания функции.

Следующий способ задания функции применяется чаще всего на практике называется табличный.

Все данные представлены в виде таблице. У этого способа имеется конечное множество значений аргумента. Такими таблицами вы уже пользовались в алгебре, например, таблица квадратов, таблица корней и т.д.

Примеры, табличного задания функции:

x	1	2	3	4	5	6	7	8	9
y	1	4	9	16	25	36	49	64	81

Рассмотрим примеры по теме «Способы задания функции»:

Пример №1:

Является ли графическим заданием какой-либо функции фигура?

Сколько бы мы не проводили вертикальных линий, всегда будет одно пересечение с графиком. Следовательно, изображенная фигура является графиком функции.

Пример №2:

Является ли графическим заданием какой-либо функции фигура?

Сколько бы мы не проводили вертикальных линий, всегда будет одно пересечение с графиком. Следовательно, изображенная фигура является графиком функции.

Пример №3:

Является ли графическим заданием какой-либо функции фигура?

При проведении вертикальных линий у нас имеется два пересечения. То есть у одной вертикальной линии два пересечения с фигурой. По определению переменной x должно соответствовать только одно значение переменной y, а у нас два пересечения фигуры. Следовательно, данная фигура не является графиком функции.

Источник

Способы задания функций. График функции

Содержание

Определить правило, по которому зависимая величина будет меняться, значит задать функцию. Вариантов задания функции несколько:

1. Словесно, например: «игрек равен двум х». Запись будет выглядеть так: $у = 2\times x$
2. Аналитический способ, то есть сразу с помощью записи формулы, например: $f(x) = x-3$
3. Графический способ
4. Табличный способ

Графический способ

Графический способ подразумевает чертеж на прямоугольной координатной плоскости, например:

Линия, изображенная на рисунке, называется графиком функции.

Линия может быть разной: прямой или кривой.

Функция (и ее график) может быть:

• возрастающей (линия идет вверх, как на рисунке выше), если вторая зависимая величина увеличивается вместе с первой;
• убывающей (линия идет вниз), если вторая величина уменьшается при увеличении первой, например:

Функция (и ее график) может быть убывающей или возрастающей как на всей области определения, так и на определенном промежутке:

Графический способ не дает возможности предельно точного определения численных значений $x$ и $у$, но он наглядно показывает поведение функции (убывает или возрастает, максимум, минимум, непрерывность и т. д.) и является важным способом ее исследования.

Табличный способ

Часто используется табличный (то есть в виде таблицы) способ задания функции. В таблице для каждого значения аргумента $x$ указывается соответствующее ему конкретное значение функции $y$, например:

$x$	$1$	$2$	$3$	$5$
$y$	$10$	$20$	$30$	$50$

Каждое значение аргумента и функции нумеруется. В данном случае в таблице значению $x_1$ , равному $1$ , соответствует единственное значение $у_1$ , равное $10$ . Значению $x_2$ , равному $2$ , соответствует $у_2$ , равное $20$ и т. д.

Не трудно догадаться, что в таблице выше отражена зависимость

Ее можно продолжить для любых значений $x$, так при

$y_<100>$ будет равен $1000$.

Табличный способ позволяет быстро найти конкретные значения $x$ и $у$.

Заполним таблицу для функции

Попробуем заполнить таблицу функции $у=3x+2$, для значений $x$, равных $1$, $3$, $4$, $8$.

Подставим в формулу $у=3x+2$ значения $x_1$, $x_2$, $x_3$, $x_4$.

Источник