Способы задания функции 7 класс алгебра макарычев

Что такое Функция?

О чем эта статья:

7 класс, 11 класс, ЕГЭ/ОГЭ

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

• х ≠ 0 (потому что на ноль делить нельзя)

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник

Способы задания функции 7 класс алгебра макарычев

Если Вы не нашли темы для своего учебника, то можете добавить оглавление учебника и получить благодарность от проекта «Инфоурок».

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

В Северной Осетии организовали бесплатные онлайн-курсы по подготовке к ЕГЭ

Время чтения: 1 минута

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

Российские школьники завоевали пять медалей на олимпиаде по физике

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Конспект урока по алгебре для 7 класса на тему «График функции»

Конспект урока по алгебре для 7 класса

на тему «График функции»

Учебник: Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова «Алгебра. 7 класс»

Тип урока: объяснение нового материала

1. Образовательная: ввести понятие «график функции», формирование умений строить график функции и читать его, формирование умений определять по графику соответствующие значения аргумента и функции.

2. Развивающая : способствовать развитию интеллектуальных навыков: сравнение, классификация, анализ; развитию коммуникативных навыков.

3. Воспитательная : воспитывать диалоговую культуру, любовь к предмету.

Устная работа. Фронтальная работа с классом

1.Приведите пример функциональной зависимомти одной переменной от другой.

Укажите независимую и зависимую переменные.

2.Как называется независимая переменная?

3.Как называется зависимая переменная?

4.Какие способы задания функции вы знаете?

5.Функция задана формулой у = 3х — 10. Найдите значение функции, соответствующее значению аргумента, равного а) – 1 б) 0 в) 2

6. Функция задана формулой у = 4 – 0,5х. Найдите значение аргумента, которому соответствует значение функции, равное 4.

7.Какие из графиков задают функцию?

3. Изучение нового материала

Фронтальная работа с классом.

(п.14 учебника до примера 1)

(определение графика функции стр.63)

Рассматриваем пример 1.

Коллективная выработка алгоритма построения графика функции:

По выбранным значениям одной величины (аргумента х) вычисляют значения другой величины (аргумента у)

На координатной плоскости отмечают точки с соответствующими координатами (х;у)

Полученные точки соединяют плавной линией.

4. Тренеровочное упражнение № 283 – на доске и в тетрадях

5 .Продолжение изучения нового материала – пример 2 п. 14 и далее до конца. Знакомство с алгоритмами нахождения по графику значения функции для данного значения аргумента и решения обратной задачи.

6 . Тренеровочные упражнения.

№ 286 – с комментарием

№ 287 – (работа в парах) с комментированием, оформление может быть дано в виде таблицы

7 . Самостоятельная работа (с последующей проверкой)

8 . Подведение итогов урока.

-Что называется графиком функции?

-Что понравилось особенно?

-Что бы хотелось выполнить еще раз?

-Что не понравилось и почему?

-Что бы вы хотели изменить?

9 . Домашнее задание: п.14 изучить, решить № 283, 296 (а, в)

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 812 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 286 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 599 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-861678

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

В Северной Осетии организовали бесплатные онлайн-курсы по подготовке к ЕГЭ

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

В России выбрали топ-10 вузов по работе со СМИ и контентом

Время чтения: 3 минуты

В Осетии студенты проведут уроки вместо учителей старше 60 лет

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Урок «Что такое функция.»

Первый урок изучения функции по учебнику 7 класса Макарычев Ю. Н. «Что такое функция». Введение понятия функция. Различные способы задания функций.

Содержимое разработки

Понятие функции пронизывает все разделы математики. Это одно из самых фундаментальных понятий.

Прежде чем дать строгое определение, опишем на примерах смысл этого понятия.

Функция выражает идею зависимости величин: с изменение одной величины может меняться и другая величина.

Например, любая физическая формула выражает зависимость одной величины от другой.

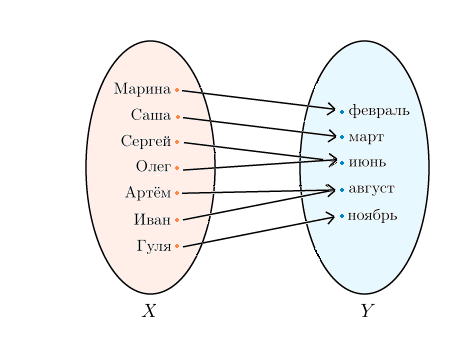
Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:

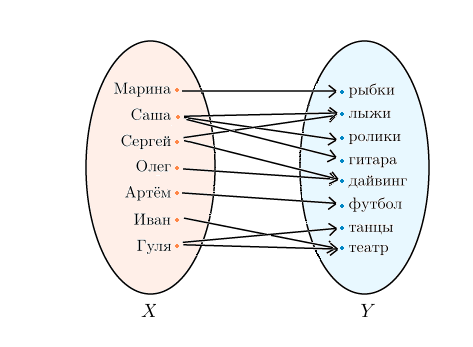
А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:

Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.

Очень сложно было бы описать такое соответствие математически, не правда ли?

Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?

Составьте выражения для решения данных задач.

Поезд движется из Москвы в Тулу со скоростью 60 км/ч. Какой путь пройдет поезд за t часов?

У покупателя 160 рублей. Сколько кг картофеля может купить покупатель по цене “в” рублей за кг?

Чему равна площадь квадрата со стороной “а” см?

4.2. Мы указали формулу, позволяющую для каждого значения одной переменной однозначно вычислить значение другой переменной.

Значения пути зависят от выбора значений времени.

Значения веса зависят от выбора значений цены.

Значения площади квадрата зависят от выбора значений длины стороны.

Попробуем сконструировать аппарат, работающий как функция. Мы закладываем в этот аппарат некоторое число “х”, аппарат срабатывает и выдает число “у”.

В наших примерах значения переменных t, в, а образно говоря мы закладывали в аппарат. Такие переменные называются независимыми переменными или аргументами. Аппарат нам выдал значения переменных S, Р, S_кв., такие переменные называются зависимыми переменными или функциями (от латинского functio – исполнение, осуществление).

Узнаёте в описании свой калькулятор.На одной кнопке написано x^2, на другой ! Нажимаете клавишу и калькулятор выполняет предписанное действие с тем числом, что вы ввели. В технической литературе часто встречается интерпретация функции как устройства, на вход которого подаётся x, а на выходе возникает у:даже в повседневной жизни мы иногда используем слово «функция» в смысле действие-например, можем говорить о функции мобильного телефона. Можем даже говорить о функции депутата.

Как же эта идея формализуется в математике. Вот строгое определение.

Но прежде чем говорить о свойствах функций поговорим о способах заданий функции.

Здесь уместно вспомнить о пословицах. Ведь пословицы – это тоже отражение устойчивых закономерностей, выверенное многовековым опытом народа. Учитель называет пословицу, учащиеся определяют зависимые и независимые величины. “Чем дальше в лес, тем больше дров”. Количество дров нарастает по мере продвижения в глубь леса – от опушек, где все давным-давно собрано, до чащоб, куда еще не ступала нога заготовителя. “Каши маслом не испортишь”.

Источник