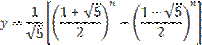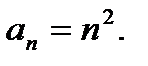Способы задания числовой последовательности



Методические указания
Определение 1.Функцию y = f(x), x 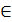
В данном случае независимая переменная – натуральное число.
Способы задания числовой последовательности
Правила задания последовательности описываются словами, без указания формул или когда закономерности между элементами последовательности нет.
Пример 1.Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, . .
Пример 2. Произвольный набор чисел: 1, 4, 12, 25, 26, 33, 39, . .
Пример 3. Последовательность чётных чисел 2, 4, 6, 8, 10, 12, 14, 16, .
Любой n-й элемент последовательности можно определить с помощью формулы.
Пример 1. Последовательность чётных чисел: y = 2n.
Пример 2.Последовательность квадрата натуральных чисел: y = n 2 ;
1, 4, 9, 16, 25, . n 2 , . .
Пример 3. Стационарная последовательность: y = C; C, C, C, . C, .
Частный случай: y = 5; 5, 5, 5, . 5, . .
Пример 4. Последовательность y = 2 n ;
2, 2 2 , 2 3 , 2 4 , . 2 n , . .
Указывается правило, позволяющее вычислить n-й элемент последовательности, если известны её предыдущие элементы.
Пример 1. Арифметическая прогрессия: a1=a, an+1=an+d, где a и d – заданные числа, d — разность арифметической прогрессии. Пусть a1=5, d=0,7, тогда арифметическая прогрессия будет иметь вид: 5; 5,7; 6,4; 7,1; 7,8; 8,5; . .
Пример 2. Геометрическая прогрессия: b1= b, bn+1= bnq, где b и q – заданные числа, b 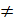
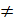
Пример 3. Последовательность Фибоначчи. Эта последовательность легко задаётся рекуррентно: y1=1, y2=1,yn-2+yn-1, если n=3, 4, 5, 6, . . Она будет иметь вид: 1, 1,2, 3, 5, 8, 13, 21, 34, 55, . .
Аналитически последовательность Фибоначчи задать трудно, но возможно. Формула, по которой определяется любой элемент этой последовательности, выглядит так:
Пример 1. Составить возможную формулу n-го элемента последовательности (yn):
а) Это последовательность нечётных чисел. Аналитически эту последовательность можно задать формулой y = 2n+1.
б) Это числовая последовательность, у которой последующий элемент больше предыдущего на 4. Аналитически эту последовательность можно задать формулой y = 4n.
Пример 2. Выписать первые десять элементов последовательности, заданной рекуррентно: y1=1, y2=2, yn = yn-2+yn-1, если n = 3, 4, 5, 6, . .
Каждый последующий элемент этой последовательности равен сумме двух предыдущих элементов.
Пример 3. Последовательность (yn) задана рекуррентно: y1=1, y2=2,yn=5yn-1— 6yn-2. Задать эту последовательность аналитически.
Найдём несколько первых элементов последовательности.
Получаем последовательность: 1; 2; 4; 8; 16; 32; 64; . которую можно представить в виде
2 0 ; 2 1 ; 2 2 ; 2 3 ; 2 4 ; 2 5 ; 2 6 . .
n = 1; 2; 3; 4; 5; 6; 7. .
Анализируя последовательность, получаем следующую закономерность: y = 2 n -1 .
Источник
Числовые последовательности и способы их задания
Числовые последовательности и способы их задания.
Определение 1. Функцию y = f ( x ), xN называют функцией натурального аргумента или числовой последовательностью и обозначают: y = f ( n ) или y 1 , y 2 , y 3 , . y n , . или ( y n ).
В данном случае независимая переменная – натуральное число.
Способы задания числовой последовательности.
Правила задания последовательности описываются словами, без указания формул или когда закономерности между элементами последовательности нет.
Пример 1. Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, . .
Пример 2. Произвольный набор чисел: 1, 4, 12, 25, 26, 33, 39, . .
Пример 3. Последовательность чётных чисел 2, 4, 6, 8, 10, 12, 14, 16, . .
Любой n -й элемент последовательности можно определить с помощью формулы.
Пример 1. Последовательность чётных чисел: y = 2 n .
Пример 2. Последовательность квадрата натуральных чисел: y = n 2 ;
1, 4, 9, 16, 25, . n 2 , . .
Пример 3. Стационарная последовательность: y = C ;
Частный случай: y = 5; 5, 5, 5, . 5, . .
Пример 4 . Последовательность y = 2 n ;
2, 2 2 , 2 3 , 2 4 , . 2 n , . .
Указывается правило, позволяющее вычислить n -й элемент последовательности, если известны её предыдущие элементы.
Пример 1 . Арифметическая прогрессия: a 1 = a , a n +1 = a n + d , где a и d – заданные числа, d — разность арифметической прогрессии. Пусть a 1 =5, d =0,7, тогда арифметическая прогрессия будет иметь вид: 5; 5,7; 6,4; 7,1; 7,8; 8,5; . .
Пример 2. Геометрическая прогрессия: b 1 = b , b n +1 = b n q , где b и q – заданные числа, b 0, q 0; q – знаменатель геометрической прогрессии. Пусть b 1 =23, q =½, тогда геометрическая прогрессия будет иметь вид: 23; 11,5; 5,75; 2,875; . .
Пример 3. Последовательность Фибоначчи. Эта последовательность легко задаётся рекуррентно: y 1 =1, y 2 =1, y n -2 + y n -1 , если n =3, 4, 5, 6, . . Она будет иметь вид:
1, 1,2, 3, 5, 8, 13, 21, 34, 55, . .
Аналитически последовательность Фибоначчи задать трудно, но возможно. Формула, по которой определяется любой элемент этой последовательности, выглядит так:
3.2. Закрепление нового материала. Решение задач.
Для закрепления знаний выбираются примеры в зависимости от уровня подготовки учащихся.
Пример 1. Составить возможную формулу n -го элемента последовательности ( y n ):
а) Это последовательность нечётных чисел. Аналитически эту последовательность можно задать формулой y = 2 n +1.
б) Это числовая последовательность, у которой последующий элемент больше предыдущего на 4. Аналитически эту последовательность можно задать формулой y = 4 n .
Пример 2 . Выписать первые десять элементов последовательности, заданной рекуррентно: y 1 =1, y 2 =2, y n = y n -2 + y n -1 , если n = 3, 4, 5, 6, . .
Каждый последующий элемент этой последовательности равен сумме двух предыдущих элементов.
Пример 3. Последовательность ( y n ) задана рекуррентно: y 1 =1, y 2 =2, y n = 5 y n -1 — 6 y n -2 . Задать эту последовательность аналитически.
Найдём несколько первых элементов последовательности.
Получаем последовательность: 1; 2; 4; 8; 16; 32; 64; . которую можно представить в виде
2 0 ; 2 1 ; 2 2 ; 2 3 ; 2 4 ; 2 5 ; 2 6 . .
n = 1; 2; 3; 4; 5; 6; 7. .
Анализируя последовательность, получаем следующую закономерность: y = 2 n -1 .
Пример 4. Дана последовательность y n =24 n +36-5 n 2 .
а) Сколько в ней положительных членов?
б) Найти наибольший элемент последовательности.
в) Есть в данной последовательности наименьший элемент?
Данная числовая последовательность – это функция вида y = -5 x 2 +24 x +36, где x
а) Найдём значения функции, при которых -5 x 2 +24 x +36>0. Решим уравнение -5 x 2 +24 x +36=0.
D = b 2 -4 ac =1296, X 1 =6, X 2 =-1,2.
Уравнение оси симметрии параболы y = -5 x 2 +24 x +36 можно найти по формуле x =, получим: x =2,4.
Неравенство -5 x 2 +24 x +36>0 выполняется при -1,2 В этом интервале находится пять натуральных чисел (1, 2, 3, 4, 5). Значит в заданной последовательности пять положительных элементов последовательности.
б) Наибольший элемент последовательности определяется методом подбора и он равен y 2 =64.
в) Наименьшего элемента нет.
1. Составьте возможную формулу n -го элемента последовательности ( y n ), если последовательность имеет вид: 2, 4, 6, 8, 10, 12, . .
2. Выписать первые десять элементов последовательности заданной рекуррентно: y 1 =1, y 2 =3, y n = y n -2 + y n -1 .
3. Найдите формулу n -го элемента и сумму первых 15 элементов арифметической прогрессии с первым элементом 3,4 и разностью 0,9.
4. Найдите сумму бесконечной геометрической прогрессии с первым членом 3,5 и знаменателем —
5 . В арифметической прогрессии a 5 = -150, a 6 = -147. Найдите номер первого положительного элемента этой последовательности.
6 . Укажите наиболее близкий к нулю элемент арифметической прогрессии
7. Дана последовательность y n =12 n + 8 — 2,5 n 2 .
а) Сколько в ней положительных элементов?
б) Найти наибольший элемент последовательности.
в) Есть в данной последовательности наименьший элемент?
Источник
СПОСОБЫ ЗАДАНИЯ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
ЧТО ИЗУЧАЕТ МАТЕМАТИЧЕСКИЙ АНАЛИЗ?
Мы приступаем к изучению раздела математики, который обычно называют «Математический анализ». Это будет первое знакомство с серьезным разделом высшей математики. В основе математического анализа лежит идея движения, изменения процесса. Он предлагает набор некоторых стандартных математических моделей, с помощью которых можно описать различные процессы, разнообразные связи между меняющимися величинами, переменными.
1. Дискретная модель – последовательность.
2. Непрерывная модель – функция, заданная формулой.
3. Модель в форме зависимости – уравнение.
4. Интегральная модель – плотность.
Таким образом, математический анализ создает модели для описания различных процессов,
исследование которых требует применения наряду с известными методами и новых операций – дифференцирования и интегрирования.
ПОНЯТИЕ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
Функция, область определения которой – множество натуральных чисел или множество первых n натуральных чисел, называется последовательностью.
Если последовательность определена на множестве всех натуральных чисел, то такую последовательность называют бесконечной, а если последовательность определена на множестве первых n натуральных чисел, то её называют конечной.
В общем виде числовая последовательность записывается в следующим образом: а1, а2, …аn.
Значения последовательности а1, а2, …аn, …называют ее членами. Обычно члены последовательности обозначают буквой с индексами. Последовательность иногда обозначают так: 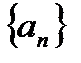
СВОЙСТВА ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Числовая последовательность – частный случай числовой функции, а поэтому некоторые свойства функций рассматриваются и для последовательностей.
Последовательность называют возрастающей, если каждый ее член (кроме первого) больше предыдущего.
Последовательность называют убывающей, если каждый ее член (кроме первого) меньше предыдущего.
Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.
Последовательность <an> называется ограниченной сверху, если существует такое число М, что для всех n ∈ N справедливо неравенство an ≤ М. Число М называется верхней границей последовательности<an>. Если последовательность ограничена сверху, то она имеет бесконечное количество верхних границ.
Последовательность<an> называется ограниченной снизу, если существует такое число m, что для всех n ∈ N справедливо неравенство an ≤ m. Число m называется нижней границей последовательности<an>.
Последовательность <an> называется ограниченной, если она ограничена снизу и сверху, то есть m ≤ an ≤ M (n ∈ N).
Последовательность, которая не будет ограниченной хотя бы снизу или хотя бы сверху, называется неограниченной.
СПОСОБЫ ЗАДАНИЯ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Последовательности можно задавать различными способами, среди которых особенно важны три: словесный, аналитический и рекуррентный.
Последовательность задана словесно, если правило задания последовательности описано словами, без указания каких-либо формул.
Говорят, что последовательность задана аналитически,еслиуказана формула ееn-го члена.
Например: 1) 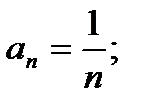
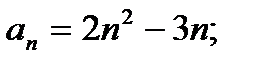

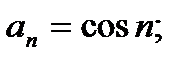
В приведенных примерах, подставляя конкретное значение n в формулу, нетрудно найти член последовательности с соответствующим номером.
Рекуррентный способ задания числовой последовательности состоит в том, что указывают правило, позволяющее вычислить n-ый член последовательности, если известны ее предыдущие члены.
Реши самостоятельно: Запишите первые 10 членов последовательности, заданной различными способами:
а) 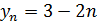
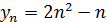
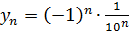
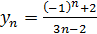
д) 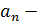
е) 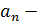
ж) 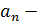
з) 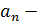
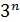
и) 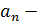

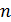
Среди рекуррентно заданных последовательностей особо выделяются:
Источник