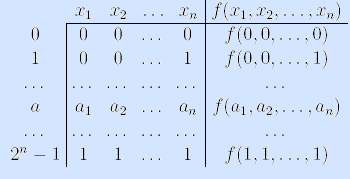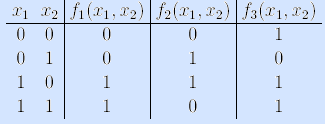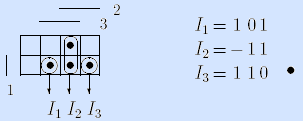Способы задания булевой функции от n переменных

Способы задания булевой функции от n переменных

1) Задание булевой функции таблицей истинности. Так называется таблица, состоящая из двух частей: в левой части перечисляются все наборы значений аргументов (булевы векторы пространства B n ) в естественном порядке, то есть по возрастанию значений чисел, представляемых этими векторами, а в правой части – значения булевой функции на соответствующих наборах.

Пример. Рассмотрим булеву функцию трех аргументов, называемую мажоритарной (или функцией голосования): она принимает значение 1 на тех и только тех наборах, в которых единиц больше, чем нулей (major – больший).

Так как левая часть таблицы истинности постоянна для всех функций с одинаковым числом аргументов, несколько таких функций могут быть заданы общей таблицей.

Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 2 2 n .

Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2 n , где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих от n переменных) равно 2 m =2 2 n . •

2) Задание булевой функции характеристическими множествами. Так называются два множества:

M 1 _f, состоящее из всех наборов, на которых функция принимает значение 1, то есть M 1 _f = <α B n :f(α) = 1>;

M 0 _f, состоящее из всех наборов, на которых функция принимает значение 0, то есть M 0 _f = <α B n :f(α) = 0>.

Пример (мажоритарная функция).

3) Задание булевой функции вектором ее значений.

Пример (мажоритарная функция).

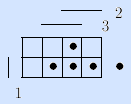
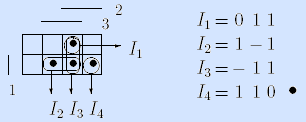
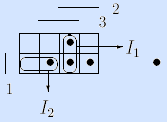
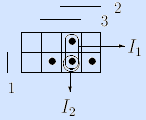
4) Задание булевой функции матрицей Грея. Булево пространство задается матрицей Грея, и наборы (клетки матрицы), на которых булева функция f(x₁, …, x_n) принимает значение 1, отмечаются и называются точками.

Пример (мажоритарная функция).

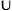
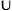
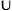
5) Интервальный способ задания булевой функции. Булеву функцию f(x₁, …, x_n) можно задать множеством интервалов I_f = 1, I₂, …, I_k>, объединение которых образует характеристическое множество M 1 _f, то есть I₁ I₂… I_k = M 1 _f. Множество интервалов I_f называется достаточным для функции f(x₁, …, x_n).

Пример. Мажоритарная функция может быть задана достаточным множеством I_f = 1, I₂, I₃> интервалов:

Здесь интервалы представлены троичными векторами и изображены на матрице Грея.

В отличие от предыдущих, интервальный способ задания функций многовариантен (одну и ту же булеву функцию можно представить разными множествами интервалов).

Пример. Зададим мажоритарную функцию другим достаточным множеством I’_f = 1, I₂, I₃, I₄> интервалов:

Очевидно, что это множество интервалов избыточно: первый интервал (011) можно удалить.

Определение. Интервал назовем допустимым для булевой функции, если на всех его наборах функция равна 1.

Примеры. I₁= – 1 1 – допустимый интервал для мажоритарной функции, I₂= 1 0 – – не допустимый.

Определение. Интервал I назовем максимальным для булевой функции f(x₁, …, x_n), если он является допустимым для этой функции, и не существует другого допустимого интервала I’, такого что I 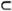I’.

Пример. I₁= –11 является максимальным интервалом для мажоритарной функции, а допустимый интервал I₂ = 111 не является максимальным, так как I₂ 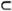I₁.

Пример. Зададим мажоритарную функцию множеством I»_f = 1 I₂, I₃> всех максимальных интервалов.

Определение. Точку булевой функции f(x₁, …, x_n) назовем ядерной, если она принадлежит ровно одному максимальному для этой функции интервалу. Максимальный интервал называется ядерным, если он содержит ядерную точку.

Пример. Для мажоритарной функции ядерными точками являются 011 (принадлежит только интервалу –11), 101 (принадлежит только интервалу 1 –1) и 110 (принадлежит только интервалу 11 –). Все максимальные интервалы этой функции являются ядерными. •

Очевидно, что все ядерные интервалы входят в любое достаточное множество функции, состоящее из максимальных интервалов.

6) Задание булевой функции формулами будет рассмотрено несколько позже.

Источник

Лекция 03. Определение и способ задания булевых функций

Булевой функцией от n аргументов называется однозначное отображение n – мерного булева куба на одномерный булев куб.

Способы задания функций

0 0 0 0 0 0 0 0 0

1 1 1 1 1 1 1 1 1

Gi — значение функции от данных аргументов.

Порядок возрастания векторов по мере возрастания их номеров называют лексикографическим.

Единичным вектором для данной функции называется тот вектор, значение функции на котором равно 1.

Носителем данной функции – совокупность всех единичных векторов этой функции (Nf – носитель функции f)

На векторах, помеченных звездочкой, функция обращается в 1.

Nf = <001, 011, 100, 110>= [1,3,4,6] [] – указаны номера векторов.

3. В виде формулы.

Функция f зависит от переменной xi фиктивно, если для любых двух наборов значений переменных, отличающихся только значением переменной xi, значения функции f совпадают.

Будем говорить, что f зависит от переменной xi существенно, если существуют такие два набора значений, отличающихся только значением переменной xi, на которых значения функций различно.

Фиктивные переменные у функции можно добавлять и исключать.

Две булевы функции называются равными или равносильными, если одну можно получить из другой путем добавления и изъятия фиктивных переменных.

Источник

Способы задания булевой функции от n переменных

называемое номером набора y. Например, двоичные наборы 101 и 111 имеют номера 5 и 7 соответственно. Очевидно, любая булева функция может быть задана таблицей истинности, в которой двоичные наборы заменены своими номерами (табл. 1.2).
Булевы функции, зависящие от большого числа переменных, задавать таблицей истинности неудобно в силу ее громоздкости. Например, таблица истинности булевой функции 8 переменных будет содержать 2 8 = 256 строк. Поэтому для задания функций многих переменных удобно использовать модификацию таблицы истинности.
Рассмотрим способ построения такой таблицы истинности для функции n переменных. Множество из n переменных функции разбивается на два подмножества: х₁, х₂, . х_j-1 и х_j, х_j+1, . х_n. Переменными x₁, x₂, . x_n отмечают строки таблицы истинности, задавая в каждой строке значение соответствующего двоичного набора длины j-1. Переменными x_j, x_j+i, . x_n отмечают ее столбцы, задавая в каждом столбце значения соответствующего двоичного набора длины n-j+1. Значение функции записывается в клетке на пересечении соответствующей строки и столбца (табл. 1.3).

Таблица 1.3
x1,x2. xj-1	xj, xj+1, . xn
	00. 0	0. 1	.	11. 1
00. 0	.
00. 1	.
.	.	.	.	.
11. 1

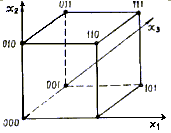
При геометрическом способе булева функция f (х₁, . х_n) задается с помощью n-мерного куба. В геометрическом смысле каждый двоичный набор у = y_i E <0,1>есть n-мерный вектор, определяющий точку n-мерпого пространства. Исходя из этого, все множество наборов, на которых определена функция n переменных, представляется вершинами n-мерного куба. Отмечая точками вершины куба, в которых функция принимает единичное (либо нулевое) значение, получим геометрическое представление функции. Например, булева функция, заданная табл. 1.1, геометрически представляется 3-мерным кубом (рис. 1).

При аналитическом способе булева функция задается формулами, т. е. аналитическими выражениями, построенными на основе операций булевой алгебры. Аналитический способ задания булевых функций занимает особое место в проектировании цифровых автоматов. Фактически, все преобразования над булевыми функциями, необходимые для построения цифровых автоматов, ведутся на аналитическом уровне.
Рассмотрим области определения булевых функций. Как уже отмечалось, между двоичными наборами и двоичными числами существует взаимно однозначное соответствие. Следовательно, существует 2 n различных наборов двоичных переменных.
Таким образом, областью определения булевой функции n переменных при матричном способе задания является множество всех возможных двоичных наборов длины n, а при геометрическом способе задания — множество всех вершин n-мерного единичного куба.
Булеву функцию, определенную на всех своих наборах, называют полностью определенной. В табл. 1.1, 1.2 приведены примеры полностью определенных булевых функций.
Булеву функцию n переменных называют неполностью определенной или частичной, если она определена не на всех двоичных наборах длины n. Неполностью определенная булева функция не попадает под определение, данное в начале , но при произвольном доопределении (на всех наборах, на которых она не определена) это несоответствие снимается.
Легко убедиться, что если булева функция f не определена на m наборах аргументов, то путем ее доопределения можно получить 2 m различных полностью определенных функций. В табл. 1.5 приведен пример неполностью определенной булевой функции трех переменных.

Таблица 1.5
х1х2х3	F
000 001 010 011 100 101 110 111	0 1 — 0 1 — 1 —

Существует не более чем 2 2^n различных булевых функций n переменных. К этому выводу легко прийти, пользуясь простыми комбинаторными рассуждениями, и вспомнив, что на каждом из 2 n наборов функции могут принимать два значения.
Функции двух переменных представлены в табл. 1.6.
Наиболее часто употребляются следующие:

Таблица 1.6
х1х2	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
00 01 10 11	0 0 0 0	0 0 0 1	0 0 1 0	0 0 1 1	0 1 0 0	0 1 0 1	0 1 1 0	0 1 1 1	1 0 0 0	1 0 0 1	1 0 1 0	1 0 1 1	1 1 0 0	1 1 0 1	1 1 1 0	1 1 1 1

f0 (x1, x2) = 0 — тождественный ноль (константа 0);
f1 (x1, x2) = x1 * x2 — конъюнкция. Вместо знака «*» иногда употребляется знак & или /\. Эту функцию часто называют логическим произведением или логическим умножением;
f3 (x1, х2) = x1 — повторение x1;
f5 (x1, x2) = x2 — повторение х2;
f6 (x1, x2) = х1 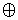x2 — сложение по модулю 2 или сумма mod 2 (далее +);
f7 (х1, х2) = x1 V x2 — дизъюнкция (логическое ИЛИ);
f8 (x1, x2) = x1 | х2 — функция Вебба (стрелка Пирса);
f9 (х1, х2) = x1

x2 — эквивалентность;
f13(x1, x2) = x1 —> x2 — импликация;
f14(x1, x2) = x1\x2 — штрих Шеффера;
f15(x1, x2) = 1-тождественная единица (константа 1).

Рассмотренные простейшие булевы функции позволяют строить новые булевы функции с помощью обобщенной операции, называемой операцией суперпозиции. Фактически операция суперпозиции заключается в подстановке вместо аргументов других булевых функций (в частности аргументов). Например, из функции f1 (x1, x2) с помощью подстановки f3 (х4, x8), f2 = x3 вместо аргументов х1 и х2 соответственно получаем функцию f1 (f3 (x4, x8), x3). Последняя от переменных х1, и х2 уже не зависит.
Отметим, что реально элементарной функции соответствует реализующий ее элемент, а суперпозиции булевых функций соответ-ствует соединение элементов

Источник