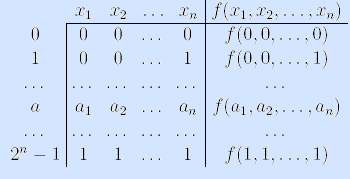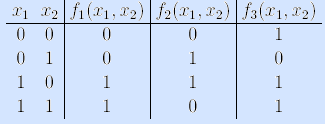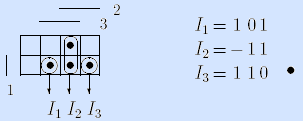Электроника
Булевы функции. Способы задания Булевых функций
Все логические схемы, используемые в цифровой электронике, являются прямой реализацией той или иной Булевой функции, то есть прежде чем сконструировать такое устройство, его необходимо математически описать. Это математическое описание всегда начинается с построения Булевых функций, т.е. для определенной комбинации двоичных переменных задается значение Булевых функций.
Задать Булеву функцию – это указать, при каких комбинациях переменных она равна 0, а при каких равна 1.
F = F(A,B,C,…), где A,B,C,… — аргументы функции ϵ <0,1>;
F – результат или сама функция ϵ <0,1>.
Каждую комбинацию аргументов называют набором. Каждому набору присваивается номер. Общепринято номер набора считать равным числу, отображаемому в скобках двоичными переменными.
Пример: набор равен 5 (n=5)
Описываем функцию F для набора: F=F(1,0,1); (A,C = 1, B = 0).
Если функция задана во всех наборах, то такую функцию называют полностью определенной. Если функция задана только в части наборов, то ее называют недоопределенной (или факультативной).
Факультативными называют условия, когда для неопределенных наборов ее можно задать по своему усмотрению. Когда функция задана, дальнейшие ее преобразования опираются на основные теоремы Булевой алгебры.
Порядок выполнения логических операций в конечном выражении полностью соответствует принятому в классической алгебре, за следующими двумя исключениями:
а) Если инверсия только над одной переменной, то она всегда выполняется первой;
б) Если инверсия над алгебраическим выражением, то она выполняется в рамках данного приложения последней.
При этом знак равенства указывает только на то, что левые и правые части от него тождественны.
Существуют следующие способы задания Булевых функций:
1. Словесный (описательный) способ – функция задается в виде текста.
Пример: F(A,B,C)=1, если аргументы в данном наборе имеют нечетное количество единиц (или если два любых аргумента функции равны 0).
2. Табличный способ задания Булевой функции – строится таблица истинности, в которой указываются номера наборов, соответствующее состояние аргументов и значение самой функции.
Например: зададим табличным способом Булеву функцию из трех аргументов, которая принимает значение единицы при четном значении нулей аргументов:
Источник
Способы задания булевой функции краткое описание
1) Задание булевой функции таблицей истинности. Так называется таблица, состоящая из двух частей: в левой части перечисляются все наборы значений аргументов (булевы векторы пространства B n ) в естественном порядке, то есть по возрастанию значений чисел, представляемых этими векторами, а в правой части – значения булевой функции на соответствующих наборах.
Пример. Рассмотрим булеву функцию трех аргументов, называемую мажоритарной (или функцией голосования): она принимает значение 1 на тех и только тех наборах, в которых единиц больше, чем нулей (major – больший).
Так как левая часть таблицы истинности постоянна для всех функций с одинаковым числом аргументов, несколько таких функций могут быть заданы общей таблицей.
Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 2 2 n .
Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2 n , где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих от n переменных) равно 2 m =2 2 n . •
2) Задание булевой функции характеристическими множествами. Так называются два множества:
M 1 f, состоящее из всех наборов, на которых функция принимает значение 1, то есть M 1 f = <α 
M 0 f, состоящее из всех наборов, на которых функция принимает значение 0, то есть M 0 f = <α 
Пример (мажоритарная функция).
3) Задание булевой функции вектором ее значений.
Пример (мажоритарная функция).
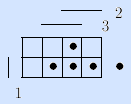
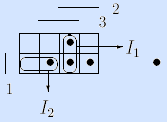
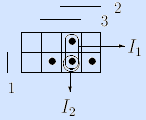
4) Задание булевой функции матрицей Грея. Булево пространство задается матрицей Грея, и наборы (клетки матрицы), на которых булева функция f(x1, …, xn) принимает значение 1, отмечаются и называются точками.
Пример (мажоритарная функция).
5) Интервальный способ задания булевой функции. Булеву функцию f(x1, …, xn) можно задать множеством интервалов If = 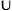
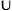
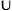
Пример. Мажоритарная функция может быть задана достаточным множеством If =
Здесь интервалы представлены троичными векторами и изображены на матрице Грея.
В отличие от предыдущих, интервальный способ задания функций многовариантен (одну и ту же булеву функцию можно представить разными множествами интервалов).
Пример. Зададим мажоритарную функцию другим достаточным множеством I’f =
Очевидно, что это множество интервалов избыточно: первый интервал (011) можно удалить.
Определение. Интервал назовем допустимым для булевой функции, если на всех его наборах функция равна 1.
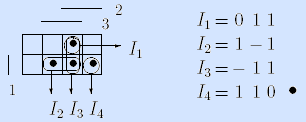
Примеры. I1= – 1 1 – допустимый интервал для мажоритарной функции, I2= 1 0 – – не допустимый.
Определение. Интервал I назовем максимальным для булевой функции f(x1, …, xn), если он является допустимым для этой функции, и не существует другого допустимого интервала I’, такого что I 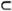
Пример. I1= –11 является максимальным интервалом для мажоритарной функции, а допустимый интервал I2 = 111 не является максимальным, так как I2 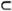
Пример. Зададим мажоритарную функцию множеством I»f =
Определение. Точку булевой функции f(x1, …, xn) назовем ядерной, если она принадлежит ровно одному максимальному для этой функции интервалу. Максимальный интервал называется ядерным, если он содержит ядерную точку.
Пример. Для мажоритарной функции ядерными точками являются 011 (принадлежит только интервалу –11), 101 (принадлежит только интервалу 1 –1) и 110 (принадлежит только интервалу 11 –). Все максимальные интервалы этой функции являются ядерными. •
Очевидно, что все ядерные интервалы входят в любое достаточное множество функции, состоящее из максимальных интервалов.
6) Задание булевой функции формулами будет рассмотрено несколько позже.
Источник
12.1. Способы задания булевой функции
Пусть х 1 , х 2 , . , х n – некоторые булевы переменные , т. е. переменные, принимающие значение из множества <0, 1>. Упорядоченную совокупность булевых переменных ( х 1 , х 2 , . , х n ) можно рассматривать как n -компонентный булев вектор х . Число компонент вектора определяет его длину, или размерность . При фиксации значений всех переменных получается набор значений переменных ( х 1 , х 2 , . х n ), задаваемый булевым вектором длины n , состоящим из констант 0 и 1. Очевидно, 2 п – число всех таких векторов. Они образуют булево пространство . Булевой функцией называется функция
f : <0, 1>n → <0, 1>. Областью определения булевой функции является булево пространство М = <0, 1>n , областью значений – множество <0, 1>.
Задание булевой функции f на булевом пространстве М делит его на две части: M f 1 – область, где функция принимает значение 1, и M f 0 – область, где функция принимает значение 0. Множество M f 1 называется
характеристическим множеством функции f .
Универсальным способом задания для любой дискретной функции является табличный способ. Таблица, представляющая функцию и называемая таблицей истинности , имеет два столбца. В левом столбце перечислены все наборы значений аргументов, в правом столбце – соответствующие им значения функции. Примером задания булевой функции от трех аргументов является табл. 12.1.
Таблица 12.1 Задание функции f ( x 1 , x 2 , x 3 )
f ( x 1 , x 2 , x 3 )
Для задания булевой функции можно ограничиться перечислением элементов ее характеристического множества M f 1 . Множество M f 1 задается булевой матрицей, строки которой представляют элементы этого множества.
Следующая матрица, задающая приведенную выше функцию, является матричным способом представления булевой функции:
Компактность представления характеристического множества M f 1 можно повысить, используя троичные векторы , компоненты которых могут принимать в качестве своих значений кроме символов 0 и 1 также символ «–». В этом случае значения булевой функции будут задаваться не на отдельных элементах, а на интервалах пространства переменных х 1 , х 2 , . х n . Чтобы
определить понятие интервала булева пространства, введем отношение ≤ на
множестве булевых векторов.
а = ( а 1 , а 2 , … , а п )
и b = ( b 1 , b 2 , … , b п )
i = 1, 2, … , п , в противном случае они несравнимы .
При этом считается, что
0 ≤ 1. Тогда интервалом булева пространства называется множество векторов, среди которых есть минимальный и максимальный векторы, а также все векторы, меньшие максимального и большие минимального. Интервал представляется троичным вектором, который задает множество всех булевых векторов, получаемых заменой символа «–» на 1 или 0.
Троичная матрица эквивалентна булевой матрице, получаемой из нее заменой каждой троичной строки на представляемую ею совокупность булевых строк с последующим устранением повторяющихся строк. Приведенная выше булева матрица оказывается эквивалентной троичной матрице
которая представляет ту же булеву функцию f ( x 1 , x 2 , x 3 ). Такой способ задания булевой функции называют еще интервальным . Представление булевой функции троичной матрицей не однозначно, т. е. для одной и той же булевой матрицы существует в общем случае не одна эквивалентная ей троичная матрица.
Две троичные матрицы эквивалентны , если они эквивалентны одной и той же булевой матрице, т. е. если они представляют одну и ту же булеву функцию.
Векторное задание булевой функции представляет собой булев вектор, компоненты которого соответствуют наборам значений аргументов. Эти наборы упорядочиваются обычно согласно порядку чисел, двоичные коды которых они представляют. Рассмотренная выше булева функция f ( x 1 , x 2 , x 3 ) представляется вектором (01 1 1 0 1 0 1), показывающим, что функция принимает значение 0 на наборах (00 0), (1 0 0), (1 1 0) и значение 1 на наборах (0 0 1), (0 1 0), (0 1 1), (1 0 1), (1 1 1). Заметим, что этот вектор совпадает с правым столбцом табл. 12.1.
Если значения булевой функции определены для всех 2 n наборов значений вектора x , она называется полностью определенной , в противном случае – не полностью определенной , или частичной . Задание не полностью определенной булевой функции f разбивает булево пространство на три множества: кроме M f 1 и M f 0 в нем присутствует множество M f – , где значения функции f не определены. Для задания частичной булевой функции необходимо задать не менее двух множеств. Обычно это M f 1 и M f 0 .
Далее будет рассмотрен алгебраический способ задания булевой функции.
12.2. Элементарные булевы функции и алгебраические формы
Рассматривая векторную форму задания булевой функции, легко определить число булевых функций от п переменных – это число всех 2 n —
компонентных булевых векторов, т. е. 2 2 п . Однако это число учитывает также функции и от меньшего числа аргументов. Любую функцию от п аргументов можно считать функцией от большего числа аргументов. Для этого вводится понятие существенной зависимости и несущественной зависимости . Функция f ( х 1 , х 2 , . , х n ) существенно зависит от аргумента х i , если
f ( х 1 , х 2 , . , х i – 1 , 0, х i + 1 , … , х n ) ≠ f ( х 1 , х 2 , . , х i – 1 , 1, х i + 1 , … , х n ).
Переменная х i в этом случае называется существенным аргументом . В
противном случае она является несущественным или фиктивным аргументом .
Элементарными булевыми функциями являются функции от одной и двух
переменных. Число функций от одной переменной равно 2 2 1 = 4. Эти функции представлены в табл. 12.2. Две из них, f 0 и f 3 , являются константами 0 и 1, переменная x для них является несущественным аргументом. Функция f 1 также является тривиальной, любое ее значение совпадает со значением аргумента: f 1 ( x ) = x . Нетривиальной функцией является функция f 2 ( x ) = x , называемая отрицанием , или инверсией . Ее значение всегда противоположно значению аргумента x . Из табл. 12.2 видно, что 0 = 1 и 1 = 0.
В табл. 12.3 приведены все булевы функции f i ( х 1 , х 2 ) от двух аргументов. В левом столбце показаны их выражения в терминах нескольких функций, принятых за основные.
Таблица 12.2 Булевы функции от одного аргумента
Источник