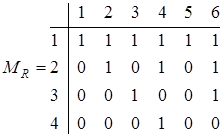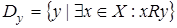Области определения и значений. Способы задания бинарных отношений
Способы задания бинарных отношений
Бинарное отношение можно задать различными способами:
1) Перечислить все пары, связанные между собой отношением.
2) Указать общие свойства, характеризующие данное отношение. Это наиболее общий способ, позволяющий задать практически любые отношения.
3) Графический способ, или задание отношения с помощью графа. В этом случае элементы множеств X и Y обозначаются точками, а элементы, связанные отношениями, соединяются направленными стрелками (рис. 2.1а). В случае 
рисуется одно множество (рис. 2.1б).
 |   |
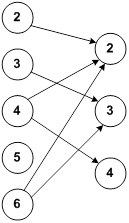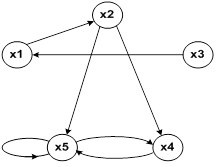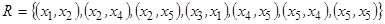| а) | б) |
| Рис.2.1. Граф бинарного отношения |
4) Матричный способ. При этом отношение описывается матрицей, количество столбцов которой соответствует количеству элементов множества X, а строк – Y. Элемент матрицы, находящийся на пересечении j столбца и i строки равен 1, если соответствующие элементы множеств X и Y связаны бинарным отношением, и 0 — в противном случае.
Если отношение R задано в множестве X, то матрица будет квадратной.
Если в матрице отношения возникает нулевой столбец, то это значит, что соответствующий элемент не связан ни с одним другим элементом этим отношением. То же самое можно сказать про нулевую строку.
Область определения отношения R – это подмножество всех элементов х множества Х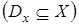 
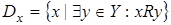
,для которыхнайдется элемент y, связанный с данным элементом отношением R.
.
Область значения отношения R – подмножество всех элементов y множества У, для которых найдутся элементы x, связанные с y отношением R (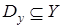
).
Пример:   |  |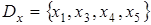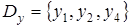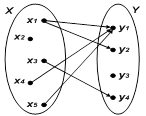
Если область определения отношения совпадает с некоторым множеством X, то говорят, что отношение определено на X.
Заслуживают внимания три частных случая отношений в Х:
1) полное (универсальное) отношение Р = Х ´ X, которое имеет место для каждой пары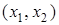 
элементов из Х (например, отношение «учиться в одной группе» на множестве студентов данной группы);
2) тождественное (диагональное) отношение Е, равносильное х=х (например, равенство на множестве действительных чисел);
3) пустое отношение, которому не удовлетворяет ни одна пара элементов из Х (например, отношение «быть братом» на множестве женщин).
Полному отношению соответствует матрица, все клетки которой заполнены единицами, тождественному — единичная матрица, пустому — нулевая матрица. Графы полного, тождественного и пустого отношений изображены на рис. 2.2 (для пустого отношения граф состоит из изолированных вершин).
Источник
Способы задания бинарных отношений
Для задания бинарных отношений можно использовать любые способы задания множеств (например, список пар, для которых данное отношение выполняется).
Бинарные отношения, определяемые на конечном множестве обычно задаются списком (пар элементов), бинарной матрицей, или ориентированным графом.
Матрица бинарного отношения, заданного на множестве 
это квадратная матрицаС порядка n, в которой 
(гдеi – номер строки, j — номер столбца) определяется так:
Для любого множества М отношение Е, заданное единичной матрицей, в которой по главной диагонали стоят “1”, а остальные “0” – называется отношением равенства.
Поскольку отношения на М задаются подмножествами множества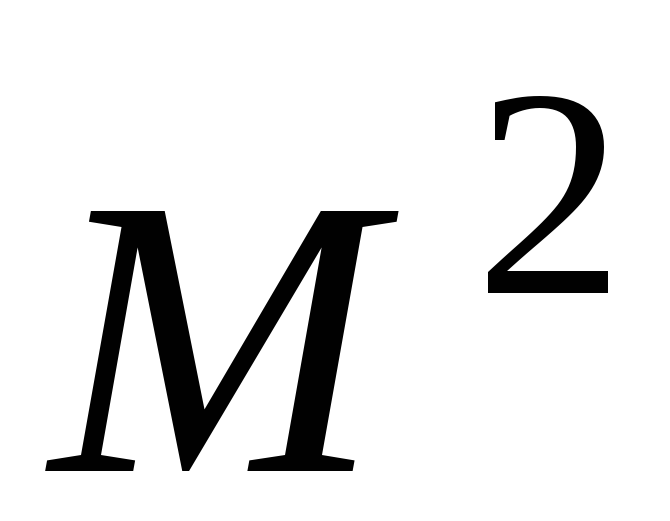 
, для них можно определить те же операции, что и над множествами.
Например, отношение “находиться на разном расстоянии от начала координат” является дополнением отношения “находиться на одинаковом расстоянии от начала координат”. Отношение “
” является объединением отношений “ 11 / 34 11 12 13 14 15 16 17 18 19 > Следующая > >>
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
Свойства бинарных отношений
Бинарное отношение на некотором множестве может обладать различными свойствами, например:
- Рефлексивность:
- Антирефлексивность (иррефлексивность):
- Корефлексивность:
- Симметричность:
- Антисимметричность:
- Асимметричность: . Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения.
- Транзитивность:
- Связность:
Способы задания бинарных отношений
Функциональное отношение
Функциональное отношение в теории множеств — это такое бинарное отношение между двумя множествами, при котором каждому элементу первого множества может соответствовать не больше одного элемента второго множества.
Источник
