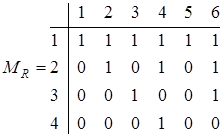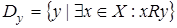Способы задания бинарных отношений с примерами

Области определения и значений. Способы задания бинарных отношений

Способы задания бинарных отношений

Бинарное отношение можно задать различными способами:

1) Перечислить все пары, связанные между собой отношением.

2) Указать общие свойства, характеризующие данное отношение. Это наиболее общий способ, позволяющий задать практически любые отношения.

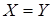
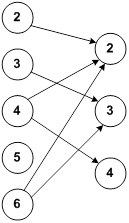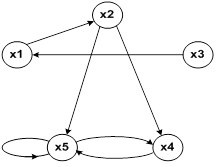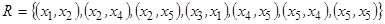3) Графический способ, или задание отношения с помощью графа. В этом случае элементы множеств X и Y обозначаются точками, а элементы, связанные отношениями, соединяются направленными стрелками (рис. 2.1а). В случае рисуется одно множество (рис. 2.1б).

а)	б)
Рис.2.1. Граф бинарного отношения

4) Матричный способ. При этом отношение описывается матрицей, количество столбцов которой соответствует количеству элементов множества X, а строк – Y. Элемент матрицы, находящийся на пересечении j столбца и i строки равен 1, если соответствующие элементы множеств X и Y связаны бинарным отношением, и 0 — в противном случае.

Если отношение R задано в множестве X, то матрица будет квадратной.

Если в матрице отношения возникает нулевой столбец, то это значит, что соответствующий элемент не связан ни с одним другим элементом этим отношением. То же самое можно сказать про нулевую строку.

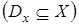
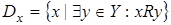
Область определения отношения R – это подмножество всех элементов х множества Х ,для которыхнайдется элемент y, связанный с данным элементом отношением R.

.

Область значения отношения R – подмножество всех элементов y множества У, для которых найдутся элементы x, связанные с y отношением R ().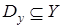

Пример: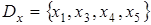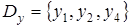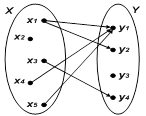

Если область определения отношения совпадает с некоторым множеством X, то говорят, что отношение определено на X.

Заслуживают внимания три частных случая отношений в Х:

1) полное (универсальное) отношение Р = Х ´ X, которое имеет место для каждой пары 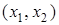элементов из Х (например, отношение «учиться в одной группе» на множестве студентов данной группы);

2) тождественное (диагональное) отношение Е, равносильное х=х (например, равенство на множестве действительных чисел);

3) пустое отношение, которому не удовлетворяет ни одна пара элементов из Х (например, отношение «быть братом» на мно­жестве женщин).

Полному отношению соответствует матрица, все клетки кото­рой заполнены единицами, тождественному — единичная матрица, пустому — нулевая матрица. Графы полного, тождественного и пустого отношений изобра­жены на рис. 2.2 (для пустого отношения граф состоит из изолиро­ванных вершин).

Источник

Лекция 3. Отношения на множествах. Свойства бинарных отношений

п.3. Отношения на множествах. Свойства бинарных отношений.

Когда говорят о родстве двух людей, например, Сергей и Анна, то подразумевают, что есть некая семья, к членам которой они относятся. Упорядоченная пара (Сергей, Анна) отличается от других упорядоченных пар людей тем, что между Сергеем и Анной есть некое родство (кузина, отец и т. д.).

В математике среди всех упорядоченных пар прямого произведения двух множеств A и B (A´B) тоже выделяются «особые» пары в связи с тем, что между их компонентами есть некоторые «родственные» отношения, которых нет у других. В качестве примера рассмотрим множество S студентов какого-нибудь университета и множество K читаемых там курсов. В прямом произведении S´K можно выделить большое подмножество упорядоченных пар (s, k), обладающих свойством: студент s слушает курс k. Построенное подмножество отражает отношение «… слушает …», естественно возникающее между множествами студентов и курсов.

Для строгого математического описания любых связей между элементами двух множеств введем понятие бинарного отношения.

Определение 3.1. Бинарным (или двухместным) отношением r между множествами A и B называется произвольное подмножество A´B, т. е.

.

В частности, если A=B (то есть rÍA2), то говорят, что r есть отношение на множестве A.

Элементы a и b называются компонентами (или координатами) отношения r.

Замечание. Договоримся, что для обозначения отношений между элементами множеств использовать греческий алфавит: r, t, j, s, w и т. д.

Определение 3.2. Областью определения бинарного отношения r называется множество Dr=<a | $ b, что arb> (левая часть). Областью значений бинарного отношения r называется множество Rr=<b | $ a, что arb> (правая часть).

Пример 3.1. Пусть даны два множества A= <1; 3; 5; 7>и B=<2; 4; 6>. Отношение зададим следующим образом t=<(x; y)ÎA´B | x+y=9>. Это отношение будет состоять из следующих пар (3; 6), (5; 4) и (7; 2), которые можно записать в виде t=<(3; 6), (5; 4), (7;2)>. В данном примере Dt= <3; 5; 7>и Rt= B=<2; 4; 6>.

Пример 3.2. Отношение равенства на множестве действительных чисел есть множество r=<(x; y) | x и y – действительные числа и x равно y>. Для этого отношения существует специальное обозначение «=». Область определения совпадает с областью значений и является множеством действительных чисел, Dr= Rr.

Пример 3.3. Пусть A – множество товаров в магазине, а B – множество действительных чисел. Тогда j=<(x; y)ÎA´B | y – цена x> – отношение множеств A и B.

Если обратить внимание на пример 3.1., то можно заметить, что данное отношение было задано сначала в виде t=<(x; y)ÎA´B | x+y=9>, а потом записано в виде t=<(3; 6), (5;4), (7;2)>. Это говорит о том, что отношения на множествах (или одном множестве) можно задавать различными способами. Рассмотрим способы задания бинарных отношений.

Способы задания отношений:

1) с помощью подходящего предиката;

2) множество упорядоченных пар;

3) в графической форме: пусть A и B – два конечных множества и r – бинарное отношение между ними. Элементы этих множеств изображаем точками на плоскости. Для каждой упорядоченной пары отношения r рисуют стрелку, соединяющую точки, представляющие компоненты пары. Такой объект называется ориентированным графом или орграфом, точки же, изображающие элементы множеств, принято называть вершинами графа.

4) в виде матрицы: пусть A=<a1, a2, …, an> и B=<b1, b2, …, bm>, r – отношение на A´B. Матричным представлением r называется матрица M=[mij] размера n´m, определенная соотношениями

.

Кстати, матричное представление является представлением отношения в компьютере.

Пример 3.4. Пусть даны два множества A=<1; 3; 5; 7>и B=<2; 4; 6>. Отношение задано следующим образом t=<(x; y) | x+y=9>. Задать данное отношение как множество упорядоченных пар, орграфом, в виде матрицы.

Решение. 1) t= <(3; 6), (5; 4), (7; 2)>— есть задание отношения как множества упорядоченных пар;

2) соответствующий ориентированный граф показан на рисунке.

3) в матричном представлении это отношение имеет вид

. ,

Пример 3.5. Еще в качестве примера можно рассмотреть предложенную Дж. фон Нейманом (1903 – 1957) блок-схему ЭВМ последовательного действия, которая состоит из множества устройств M:

,

где a – устройство ввода, b – арифметическое устройство (процессор), c – устройство управления, d – запоминающее устройство, e – устройство вывода.

Рассмотрим информационный обмен между устройствами mi и mj, которые находятся в отношении r, если из устройства mi поступает информация в устройство mj.

Это бинарное отношение можно задать перечислением всех его 14 упорядоченных пар элементов:

Соответствующий орграф, задающий это бинарное отношение, представлен на рисунке:

Матричное представление этого бинарного отношения имеет вид:

. ,

Для бинарных отношений обычным образом определены теоретико-множественные операции: объединение, пересечение и т. д.

Введем обобщенное понятие отношения.

Определение 3.3. n-местное (n—арное) отношение r – это подмножество прямого произведения n множеств, то есть множество упорядоченных наборов (кортежей)

Многоместные отношения удобно задавать с помощью реляционных таблиц. Такое задание соответствует перечислению множества n-к отношения r. Реляционные таблицы широко используются в компьютерной практике в реляционных базах данных. Заметим, что реляционные таблицы нашли применение в повседневной практике. Всевозможные производственные, финансовые, научные и другие отчеты часто имеют форму реляционных таблиц.

Слово «реляционная» происходит от латинского слова relation, которое в переводе на русский язык означает «отношение». Поэтому в литературе для обозначения отношения используют букву R (латинскую) или r (греческую).

Далее мы будем рассматривать только двухместные (бинарные) отношения, при этом опуская слово «бинарные».

Определение 3.4. Пусть rÍA´B есть отношение на A´B. Тогда отношение r-1 называется обратным отношением к данному отношению r на A´B, которое определяется следующим образом:

Определение 3.5. Пусть r ÍA´B есть отношение на A´B, а s ÍB´C – отношение на B´C. Композицией отношений s и r называется отношение t ÍA´C,которое определяется следующим образом:

Пример 3.6. Пусть , и C=<,, !, d, à>. И пусть отношение r на A´B и отношение s на B´C заданы в виде:

Найти r-1 и s◦r, r◦s.

2) Используя определение композиции двух отношений, получаем

поскольку из (1, x)Îr и (x, ,)Îs следует (1, ,)Îs◦r;

из (1, x)Îr и (x, !)Îs следует (1, !)Îs◦r;

из (1, y)Îr и (y, d)Îs следует (1, d)Îs◦r;

из (3, x)Îr и (x, !)Îs следует (3, !)Îs◦r.

Теорема 3.1. Для любых бинарных отношений выполняются следующие свойства:

1) ;

2) ;

3) — ассоциативность композиции.

Доказательство. Свойство 1 очевидно.

Докажем свойство 2. Для доказательства второго свойства покажем, что множества, записанные в левой и правой частях равенства, состоят из одних и тех же элементов. Пусть (a; b) Î (s◦r)-1 Û (b; a) Î s◦r Û $ c такое, что (b; c) Î r и (c; a) Î s Û $ c такое, что (c; b) Î r-1 и (a; c) Î s-1 Û (a; b) Î r -1◦s -1.

Свойство 3 доказать самостоятельно.

3.2. Свойства бинарных отношений.

Рассмотрим специальные свойства бинарных отношений на множестве A.

Свойства бинарных отношений.

1. Отношение r на A´A называется рефлексивным, если (a,a) принадлежит r для всех a из A.

2. Отношение r называется антирефлексивным, если из (a,b)Îr следует a¹b.

3. Отношение r симметрично, если для a и b, принадлежащих A, из (a,b)Îr следует, что (b,a)Îr.

4. Отношение r называется антисимметричным, если для a и b из A, из принадлежности (a,b) и (b,a) отношению r следует, что a=b.

5. Отношение r транзитивно, если для a, b и c из A из того, что (a,b)Îr и (b,c)Îr, следует, что (a,c)Îr.

Решение. 1) Это отношение рефлексивно, так как для каждого aÎA, (a; a)Îr.

2) Отношение не является антирефлексивным, так как не выполняется условие этого свойства. Например, (2, 2)Îr, но отсюда не следует, что 2¹2.

3) Рассмотрим все возможные случаи, показав, что отношение r является симметричным:

4) Данное отношение не является антисимметричным, поскольку (1, 2)Îr и (2,1)Îr, но отсюда не следует, что 1=2.

5) Можно показать, что отношение r транзитивно, используя метод прямого перебора.

Как по матрице представления

определить свойства бинарного отношения

1. Рефлексивность: на главной диагонали стоят все единицы, звездочками обозначены нули или единицы.

.

2. Антирефлексивность: на главной диагонали все нули.

3. Симметричность: если .

4. Антисимметричность: все элементы вне главной диагонали равны нулю; на главной диагонали тоже могут быть нули.

.

Операция «*» выполняется по следующему правилу: , где , .

5. Транзитивность: если . Операция «◦» выполняется по обычному правилу умножения, при этом надо учитывать: .

3.3 Отношение эквивалентности. Отношение частичного порядка.

Отношение эквивалентности является формализацией такой ситуации, когда говорят о сходстве (одинаковости) двух элементов множества.

Определение 3.6. Отношение r на A есть отношение эквивалентности, если оно рефлексивно, симметрично и транзитивно. Отношение эквивалентности arb часто обозначается: a

Пример 3.8. Отношение равенства на множестве целых чисел есть отношение эквивалентности.

Пример 3.9. Отношение «одного роста» есть отношение эквивалентности на множестве людей X.

Пример 3.10. Пусть ¢ — множество целых чисел. Назовем два числа x и y из ¢ сравнимыми по модулю m (mÎ¥) и запишем , если равны остатки этих чисел от деления их на m, т. е. разность (x—y) делится на m.

Отношение «сравнимых по модулю m целых чисел» есть отношение эквивалентности на множестве целых числе ¢. В самом деле:

это отношение рефлексивно, т. к. для «x΢ имеем x—x=0, и, следовательно, оно делится на m;

это отношение симметрично, т. к. если (x—y) делится на m, то и (y—x) тоже делится на m;

это отношение транзитивно, т. к. если (x—y) делится на m, то для некоторого целого t1 имеем , а если (y—z) делится на m, то для некоторого целого t2 имеем , отсюда , т. е. (x—z) делится на m.

Определение 3.7. Отношение r на A есть отношение частичного порядка, если оно рефлексивно, антисимметрично и транзитивно и обозначается символом °.

Частичный порядок важен в тех ситуациях, когда мы хотим как-то охарактеризовать старшинство. Иными словами, решить при каких условиях считать, что один элемент множества превосходит другой.

Пример 3.11. Отношение x£y на множестве действительных чисел есть отношение частичного порядка. ,

Пример 3.12. Во множестве подмножеств некоторого универсального множества U отношение AÍB есть отношение частичного порядка.

Пример 3.13. Схема организации подчинения в учреждении есть отношение частичного порядка на множестве должностей.

Прообразом отношения частичного порядка является интуитивное понятие отношения предпочтения (предшествования). Отношение предпочтения выделяет класс задач, которые можно объединить, как задача о проблеме выбора наилучшего объекта.

Формулировка задачи: пусть имеется совокупность объектов A и требуется сравнить их по предпочтительности, т. е. задать отношение предпочтения на множестве A и определить наилучшие объекты.

Отношение предпочтения P, которое можно определить как «aPb, a, bÎA Û объект a не менее предпочтителен, чем объект b» является по смыслу рефлексивным и антисимметричным (каждый объект не хуже самого себя, и, если объект a не хуже b и b не хуже a, то они одинаковы по предпочтительности). Естественно считать, что отношение P транзитивно (хотя в случае, когда, например, предпочтения обсуждаются группой лиц с противоположными интересами, это свойство может быть нарушено), т. е. P – отношение частичного порядка.

Один из возможных способов решения задачи сравнения объектов по предпочтительности – ранжирование, т. е. упорядочение объектов в соответствии с убыванием их предпочтительности или равноценности. В результате ранжирования мы выделяем «наилучшие» или «наихудшие» с точки зрения отношения предпочтения объекты.

Области применения задачи о проблеме выбора наилучшего объекта: теория принятия решений, прикладная математика, техника, экономика, социология, психология.

Источник