Бинарные операции, их свойства
В данном параграфе главной целью является изучение основ теории групп. Группа – это множество, на котором задана некоторая бинарная (зависящая от двух аргументов) алгебраическая операция, удовлетворяющая определенным условиям. Понятие бинарной алгебраической операции лежит, следовательно, в основе всего задания теории групп.
Каждому ученику средней школы, известно слово «операция» и, одним из первых его значений, приходящих в голову, являются понятия арифметических операций – сложения, умножения, вычитания или деления. Операции можно производить не только над числами, но и над другими объектами: дизъюнкции и конъюнкции высказываний, композиции преобразований и т.д.
Во всех названых примерах операций мы имеем дело с некоторым множеством А (множество чисел, высказываний, преобразований и т.д.). При выполнении операции по двум элементам этого множества находят третий элемент того же множества (по двум заданным числам находят их сумму, по двум заданным высказываниям их конъюнкцию и т.д.). При этом ответ, зависит от порядка этих элементов (например, при вычитании чисел).
Дадим определение бинарной алгебраической операции.
Определение 1. 1. 1. Пусть А – непустое множество, тогда всякое отображение φ: A × A → A называют бинарной алгебраической операцией, заданной на множестве А.
Другими словами, бинарной операцией на А является правило или закон, согласно которому каждой упорядоченной паре элементов a и b из А ставится в соответствие однозначно определенный элемент d из A (φ: (a, b)→ d). Следуя арифметической традиции, результат применения бинарной операции φ к элементам a и b обозначают a φ b и называют композицией элементов a и b. В каждом конкретном случае композиция элементов получает свое название – сумма, произведение и т.п.
Определение 1.1.2. Множество А вместе с заданной на нем бинарной алгебраической операцией * называется группоидом и обозначается .
Примеры: , , .
Нетрудно заметить, что вычитание на множестве N не является бинарной операцией. Действительно, по определению бинарной алгебраической операции должно выполнятся условие: (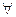 
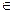
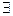
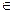
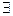
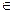
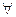
(а, b) 
N 2 ) ( 
d N 2 ) d = a – b. Составим отрицание: (а, b) N 2 ( d є N) d ≠ a – b. При a = 2, b = 3 отрицание истинно, значит исходно утверждение – ложное. Следовательно, можно утверждать, что вычитание не является бинарной операцией на множестве Nи не является группоидом.
На конечных множествах, содержащих не слишком много элементов, бинарную алгебраическую операцию удобно задавать с помощью таблицы, которая называется таблицей Кэли (А. Кэли (1821-1895) английский алгебраист). Эта таблица для группоида , A = <a1, a2, …, an> заполняется следующим образом:
| * | a1 | a 2 | … | an |
| a 1 | a1 *a1 | a1 *a2 | … | a1 *an |
| a 2 | a2 *a1 | a2 *a2 | … | a2 *an |
| … | … | … | … | … |
| an | an *a1 | an | … | an *an |
Например, следующая таблица задает операцию * на множестве A = <a , b>:
| * | a | b |
| a | b | a |
| b | b | b |
Причем a * a = b* b= b* a= b и a* b= b. Поскольку результаты операции
принадлежат А, следовательно, — группоид.
Свойства операций. Полугруппы
Известны свойства арифметических действий – переместительный (коммутативный) и сочетательный (ассоциативный) законы сложения и умножения действительных чисел. Сформулируем эти свойства для произвольной бинарной алгебраической операции. Поскольку мы рассматриваем, в определении группоида, операции на определенном множестве, то, чтобы не вводить дополнительных определений, и группоидом будем называть в соответствии с названием свойства операции.
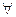
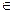
Определение 1. 1. 3. Группоид называется коммутативным (а сама операция коммутативной), если для любых двух элементов из A выполняется условие: ( a, b А) а * b = b * а.
Определение 1. 1. 4. Группоид называется ассоциативным или полугруппой (а сама операция ассоциативной), если выполняется условие:
( а, b, с А) а * (b * с) = (а* b) *с
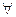
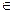
Пусть — полугруппа. Легко доказать следующие свойства.
1. (Обобщённый ассоциативный закон). Для любого конечного семейства элементов a1, . aк из А произведение a1 ?a2 . aк не зависит от расстановки скобок, т. е. от последовательности умножений по два сомножителя.
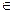
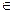
2. Естественным образом вводится понятие степени с натуральным показателем: а n = a ?a . a (n сомножителей а) для любых а А и n N, причём выполняются обычные свойства степеней:
a k+n = a k ? a n и (a k ) n = a kn (k, n 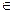N).
3. Если полугруппа коммутативна, то имеет место обобщённый коммутативный закон: произведение любого конечного числа элементов из А не зависит от порядка сомножителей.
Можно сформулировать аналогичные свойства для полугруппы .
Ещё из школы известны два правила: правило сложения любого числа с нулём и правило умножения любого числа на единицу. 0 и 1 — это нейтральные
элементы для операции сложения и умножения в R.
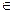
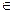
Определение 1. 1. 5. Элемент е А группоида называется нейтральным элементом, если для любого элемента a A a* e= e* a= a.
Теорема 1. 1. 1. Каждый группоид содержит не более одного нейтрального элемента.
Доказательство. Предположим, что в группоиде А существуют два различных нейтральных элемента e1 и е2. Дважды воспользовавшись определением нейтрального элемента, получим: e1 = е1 ? e2 = е2 .
Поэтому, если в группоиде существует нейтральный элемент, то он единственный.
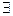
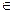
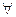
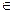
Чтобы установить, имеет ли группоид нейтральный элемент, надо выяснить, является ли группоид коммутативным, если да, то достаточно проверить одно условие: ( е А) ( а А) а * е = а. Если же нет, то надо проверять два условия: а * е = а и е * а = а.
Пример. На множестве R операция * задана правилом: a * b = a + b – 1. Покажем, что является группоидом, содержащим нейтральныйэлемент.
1. ( a, b 
R) ( ! (а + b — 1) R), следовательно, * — бинарная операция;
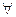
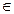
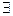
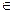
2. ( a, b R) a *b=a+b-1= b * а в силу коммутативности сложения в R;
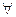
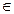
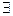
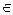
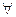
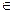
3. Условие e 
R a R a* е = а + е — 1= a выполняется при е — 1 = 0, т.к. нейтральным элементом на R относительно сложения является 0. Таким образом, е = 1 является нейтральным элементом относительно операции *.
Определение 1. 1. 6. Полугруппа с нейтральным элементом называется моноидом.
Равенства а + (— а) = 0 и а ? 1 = а напоминают нам о таких понятиях, как
противоположный и обратный элементы соответственно относительно операций сложения и умножения. Эти термины есть конкретизация такого математического понятия, как симметричный элемент. Правомерны следующие вопросы: каждый ли элемент множества имеет симметричный относительно операции в группоиде? При каких условиях элемент множества имеет симметричный?
Понятие симметричного элемента
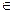
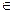
Определение 1. 1. 7. Пусть группоид имеет нейтральный элемент е, тогда элемент a A называется симметризуемым, если для него существует а’ А такой, что а* а’ = а’ * а = е. Сам элемент а’ называется в этом случае симметричным для а.
Теорема 1. 2. Если в полугруппе элемент а симметризуем, то симметричный для него элемент а’ единственный.
Доказательство. Допустим, что для а 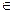А, существуют два симметричных элемента и и v. Тогда, учитывая, что дана полугруппа, получим:
Исторически сложились и существуют два языка для выражения различных фактов, касающихся бинарных алгебраических операций: мультипликативный и аддитивный.
Формы записи бинарной операции
| Произвольная | Аддитивная | Мультипликативная |
| * а * b называется композицией a’ —симметричный элемент для а е нейтральный элемент | + называется сложением а + b называется суммой -а -противоположный элемент для a нулевой элемент (нуль) | ? называется умножением а • b называется произведением а -1 — обратный элемент для а единичный элемент (единица) |
Далее в качестве основного языка выбран мультипликативный.
Источник
