Способы задания алгоритмов



Любой алгоритм становится алгоритмом лишь тогда, когда он обретает какую-либо форму. Существует несколько способов представления алгоритмов, отличающихся наглядностью, компактностью, степенью формализации и другими показателями. Наибольшее распространение получили три способа: словесно-формульный, графический и в виде последовательности команд для ЭВМ. Рассмотрим эти способы.
Словесно-формульный способ записи алгоритмов.
Его особенностью является то, что здесь допустима некоторая произвольность в обозначениях и используемых словах.
Пусть даны числа А, В, С. Найти число Н, равное большему из них.
Решение задачи можно получить, действуя следующим образом:
1. Вначале найдем большее из двух чисел, например А и В.
2. Если А ≥В, то примем Н=А, иначе (т.е. если А
Этот же алгоритм можно представить более четко, если разбить все действия на отдельные пункты. Тогда алгоритм примет вид:
1. Если А≥В, то принять Н=А и перейти к пункту 3. Иначе перейти к пункту 2.
2. Принять Н=В и перейти к следующему пункту.
3. Если Н≥С, то перейти к пункту 5, иначе перейти к следующему пункту.
4. Принять Н=С и перейти к пункту 5.
Словесно-формульный способ записи алгоритмов ориентирован прежде всего на исполнителя-человека и допускает различную запись предписаний. Но при этом запись должна быть предельно точна, чтобы человек-исполнитель мог понять суть предписаний и формально их выполнить.
Графический способ записи алгоритмов.
Данный способ предполагает использование определенных графических символов — блоков. Для придания наглядности и единообразия схем алгоритмов все графические элементы стандартизированы (ГОСТ 19.003—80. Условные графические обозначения структурных схем алгоритмов и программ). Состав, наименование, обозначение основных обязательных графических символов и отображаемые ими функции в алгоритме должны соответствовать указанным в таблице. Размер а (ширина символа) должен выбираться из ряда 10, 15, 20 мм, b=1.5*а (высота символа). Линии потока рекомендуется выполнять в два раза тоньше линий обводки блоков.
Стандартные графические элементы.
| Наименование | Обозначение блока | Содержание |
 Процесс Процесс | Выполнение операции или группы операций, в результате которых изменяются значение, форма представления или расположения данных | |
 Решение Решение | Выбор направления выполнения алгоритма или программы в зависимости от некоторых переменных условий |
 Модификация Модификация | Выполнение операций, меняющих команды или группы команд, изменяющих программу |
 Предопределенный процесс Предопределенный процесс | Использование ранее созданных и отдельно описанных алгоритмов или программ |
 Ввод-вывод Ввод-вывод | Преобразование данных в форму, пригодную для обработки (ввод) или отображения результатов обработки (вывод) |
 Документ Документ | Ввод-вывод данных, носителем которых служит бумага |
 Линии потока Линии потока | Указание на последовательность связей между символами |
 Соединитель Соединитель | Указание на связь между прерванными линиями потока, соединяющими символы |
 Пуск-остановка Пуск-остановка | Начало, конец, прерывание процесса обработки данных или выполнения программы |
  Комментарии Комментарии | Связь между элементом схемы и пояснением |
Каждый блок предписывает выполнение определенных действий. Совокупность блоков образует так называемую схему алгоритма, или блок-схему. Графический способ записи алгоритмов отличается большой наглядностью и оказывается весьма полезным на начальных стадиях разработки алгоритмов.
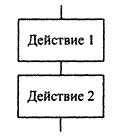
В теории программирования доказано, что для записи сколько угодно сложного алгоритма достаточно следующих структур, называемых базовыми алгоритмическими структурами (БАС). К БАС относятся:

БАС следование предполагает последовательное выполнение действий 1 и 2.
Следует отметить, что эта структура может содержать любое конечное число выполняемых действий.
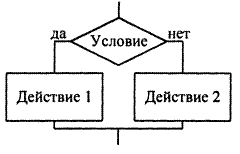
БАС логическое условие читается следующим образом: «если условие принимает значение истина, то выполняется действие 1, иначе действие 2».
В данной структуре действие 2 может отсутствовать, т.е. имеется неполное логическое условие. В этом случае, если условие принимает значение «ложь», то никакое действие не выполняется и управление передается следующему оператору.
Под циклом будем понимать многократное повторение одного или нескольких действий в соответствии с некоторым условием.
Совокупность действий, выполняемых циклом, называется телом цикла. Однократное выполнение тела цикла называется шагом или итерацией. Заметим, что условие цикла должно определяться таким образом, чтобы цикл завершал свою работу за конечное число итераций.
Циклы бывают трех видов:
· фиксированным числом шагов.
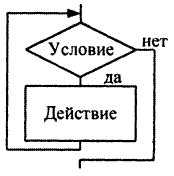
Блок-схема цикла с предусловием выглядит следующим образом:
До тех пор, пока условие принимается значение «истина» выполняются операторы тела цикла. Если условие изначально принимает значение «ложь», то действия, входящие в тело цикла, не выполняются ни разу и управление передается следующему действию.
Для цикла с постусловием условие следует за телом. При этом цикл выполняется, пока условие принимает значении «ложь». Как только оно выполняется, цикл заканчивает работу. В отличие от цикла с предусловием, цикл с постусловием всегда выполняется как минимум один раз.
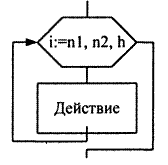
Цикл с фиксированным числом шагов является частным случаем циклов с пред- и постусловием.
Он всегда содержит специальную целочисленную переменную – счетчик, которая отсчитывает количество выполненных итераций. Значение счетчика меняется в интервале [n1, n2]. После каждой итерации значение счетчика увеличивается или уменьшается на величину шага h. Цикл заканчивает свою работу, как только счетчик достигнет определенного значения.
Представление алгоритмов в виде последовательности команд для ЭВМ.
При этом способе используются языки программирования — системы кодирования предписаний и правила их использования. По степени детализации предписаний алгоритма различают языки программирования низкого и высокого уровня.
Языки низкого уровня называются машинными кодами, поскольку программы составляются в кодах конкретной машины. При этом системы команд различных ЭВМ отличаются количеством адресов в команде, количеством разрядов, отводимых под каждый адрес, набором операций, которые может выполнять машина, и обозначений этих операций.
Языки программирования высокого уровня ориентированы не на систему команд той или иной ЭВМ, а на систему операторов, характерных для записи определенного класса алгоритмов. Например: язык Фортран (формульный транслятор) ориентирован на удобное представление формул и широко используется для инженерных и научных расчетов. Язык Паскаль разработан специально для обучения программированию и призван помогать формировать мышление программиста, естественным образом отображать структуру алгоритма в программе. Си — типичная реализация практических потребностей системного программиста, направленная на разработку новых языков — изначально создавался как инструментальное средство для реализации операционной системы UNIX. Однако его популярность переросла рамки этой системы, и в настоящее время язык Си является одним из универсальных языков программирования. Бейсик широко используется для обучения программированию и употребляется для написания простых программ.
Источник
Способы задания алгоритма — Алгоритмы — Краткий теоретический справочник
Алгоритм — заранее заданное возможному исполнителю точное предписание совершить определённую последовательность действий для получения решения задачи за конечное число шагов.
4.1. Способы задания алгоритма
На практике наиболее распространены следующие способы задания алгоритмов:
— словесный (запись на естественном языке);
— графический (изображения из графических символов);
— псевдокод (полуформализованное описание алгоритмов на условном алгоритмическом языке, включающее в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);
— программный (тексты на языках программирования).
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задаётся в произвольном изложении на естественном языке.
Пример. Запишите алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел (алгоритм Евклида).
Алгоритм может быть следующим:
1) Задать два числа.
2) Если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма.
3) Определить большее из чисел.
4) Заменить большее из чисел разностью большего и меньшего из чисел.
5) Повторить алгоритм с шага 2.
Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи.
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление называется схемой алгоритма, или блок-схемой. В блок-схеме каждому типу действий соответствует геометрическая фигура, представленная в виде блочного символа. В таблице приведены наиболее часто употребляемые символы.
Начало, конец алгоритма, входи выход в подпрограмму
Вычислительное действие или последовательность действий
Вычисления по подпрограмме
Ввод-вывод в общем виде
Блок «процесс» применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.
Блок «решение» используется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок «модификация» используется для организации циклических конструкций. Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Блок «предопределённый процесс» используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам. В псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых однозначно определён. Например, алгоритмы на алгоритмическом языке записываются с помощью служебных слов, представленных в таблице 1.8.
Таблица 1.8. Служебные слова алгоритмического языка.
Источник
Основные определения, свойства и способы задания
А существует ли алгоритм любви?
Понятие алгоритма принадлежит не только к фундаментальным научным понятиям, но и к человеческим приобретениям. Мы в окружении разнообразия алгоритмов во всех сферах жизни и деятельности. Наши действия во многом доведены до автоматизма и мы неосознаем, что они уже регламентированы тем или иным алгоритмом. Так жизнь каждого из нас состоит из выполнения повседневных алгоритмов, начиная с усвоения алгоритмов в детстве, от складывания пирамидки, и заканчивая поиском алгоритмов для решения научных проблем. Вообще любую человеческую деятельность можно подать в виде алгоритмического процесса. Авторы обзора основных открытий теории алгоритмов [1] утверждают: «Алгоритмические концепции играют в процессе обучения и воспитания современного человека фундаментальную роль, в сравнении лишь с ролью письменности».
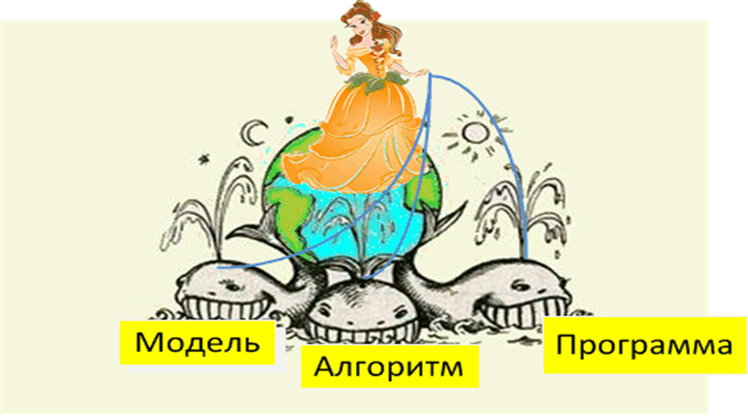
На одной из научных конференций по информатике ( 1984 г.) академик А. А. Самарский изобразил на слайде информатику в виде красавицы, что несется по научному океану на трёх китах. Имена этих китов: Модель, Алгоритм, Программа.
Центральный кит — теория алгоритмов, соединившись с математической логикой, составляют теоретический фундамент современных компьютерных наук.
И хотя интуитивно понятие алгоритма понятно, наверно, каждому, формально определить этот объект в нетривиальной теории алгоритмов совсем не так просто, как кажется на первый взгляд.
Во-первых, настораживает чрезмерная популярность этого понятия и, как в таких случаях говорят, его расширенное разъяснение. Так, вам могли встретиться такие различные алгоритмы как: “алгоритм Эвклида“, “алгоритм шахматиста“, “алгоритм поиска информации“, “алгоритм, как стать красавицей“ и другие.
Во-вторых, алгоритмы, как сами по себе, суть объекты специфического типа, которые тяжело описать математически. Они имеют нетиповое для математических объектов свойство, а именно семантическое свойство “иметь содержание“. В этом отношении теория алгоритмов подобна математической логике. С семаническими объектами, которые несут в себе содержание, математики, еще не привыкли работать. Смысл терма или формулы в математической логике “указательный“: терм указывает на вещь (т.е.помечает), а формула — на факт. Смысл алгоритма “приказной“: алгоритм должен быть выполнен. Таким образом, теория, которая изучает алгоритмы, может трактоваться как своего рода лингвистика приказных пропозиций.
И, в-третьих, теория алгоритмов возникла на стыке математики и информатики. Поэтому ученые с двух сторон “тянули на себя одеяло“ при построении теории алгоритмов. Эту специфику можно заметить, изучая монографии и пособия по теории алгоритмов. В зависимости от того, кем они написаны — математиками или знатоками информатики, мы чувствуем особенности содержания материала, отображенного в них 5.
Сейчас слово “алгоритм“ как научный термин вышло за границы математики. Этот термин используется в самых различных областях науки и техники, понимая при этом точно сформулированное правило, назначение которого – руководить действиями для достижения необходимого результата.
10.1. Понятие алгоритма. Эволюция толкования и характеристики
Понятие “ алгоритм “ — концептуальная основа различных процессов в информатике. Именно наличие алгоритмов и обеспечивает мозможность автоматизации. Больше того, значительной мерою теория алгоритмов домогает проникать математическим методам во все сфери жизни и науки, даже биологию, лингвистику,экономику аж до философии природоведения [ 1-12].
Понятие алгоритма формировалось с давних времен и до тридцатых годов ХХ ст., в научных кругах сложилось интуитивное представление про этот объект.
Одним из самых давних алгоритмов, в его интуитивном понимании, как конечной последовательности элементарных действий, которые решают поставленное задание, считается алгоритм наибольшего общего делителя двух чисел (алгоритм Эвклида). Отметим, что в течении продолжительного времени, аж до начала XX столутия, термин “алгоритм“ употреблялся только в стойком словосочетании “алгоритм Эвклида“, хотя исторически установлено, что задолго до Эвклида этот алгоритм был уже известен, например, Аристотелю.
Содержательные явления, которые привели к появлению понятия “алгоритм“, наблюдаются в математике на протяжении всего периода его существования. Именно слово “алгоритм“, как утверждают историки и математики, появилось несколько столетий тому и означало не термин, а имя. Узбекский математик Аль—Хорезми, учений, которому математика и человечество обязаны многими открытиями, был известен европейским математикам в латинской транскрипции как Алгоризми. А полное его имя — Абу Абдулла Абу Джафар Мухаммад ибн Муса аль-Хорезми (около 780 г. — около 850 г.) — в переводе буквально — отец Абдулли, Мухаммед, син Муси, уродженець Хорезми. Его книга — “Хисаб аль-джабр у аль-мукабаля“ . Именно из трактата Аль-Хорезми из арифметики началось знакомство Европы с алгоритмами — строгими процедурами для выполнения арифметичних операций. То есть алгоритм, точнее алгоризм, понямали как руководство для выполнения заданий.
Дальнейшее развитие математики утвердило мысль, что решение какой-либо проблемы должно быть алгоритмичным. Р. Декарт, Г. Ф. Лейбниц, Д. Гильберт стимулировали алгоритмические исследования. В 1900 на Втором межнародном конгрессе математиков (Париж) Давид Гильберт сформулировал 23 важные математические проблемы, находжение алгоритма решения которых, по его мнению, способствовало бы дальнейшему развитию математики.
Именно в то время были распространены две точки зрения :
1. Все проблемы являются алгоритмично решимыми. Просто еще не существует знаний для построения алгоритма.
2. Существуют классы заданий, для решения которых вообще не существует алгоритмов. Это очень сильное утверждение, потому что оно распространяется на все будущее.
Для доказательства не существования алгоритма необходимо было иметь его точное математическое определение, поэтому после того, как сформулировали понятие алгоритма как новой и отдельной сущности, первоочередной стала проблема нахождение адекватных формальных моделей алгоритма и исследование их характеристик. Формальные модели были предложены как для первичного понятия алгоритма, так и для производного понятия алгоритмично вычислительной функции. Впервые алгоритм как термин появился в работах Э. Бореля (1912) и Г. Вейля (1921).
Начальной точкой отсчета современной теории алгоритмов можно считать работу немецкого математика Курта Гьоделя (1931 год — теорема про неполноту символьних логик), в которой было показано, что для любой непротиворечивой системе аксиом существует утверждение, которое в рамках принятой аксиоматичной системы не может быть ни доказано, ни опровергнуто. Возникшее в связи с этой теоремой предположение про невозможность алгоритмического решения многих математических проблем (в том числе, проблемы выведения в вычислении предикатов) вызвало необходимость уточнения понятия алгоритма.
Первые фундаментальные работы по теории алгоритмов были опубликованы независимо в 1935-37 годах А. Тюрингом, А. Черчем, С. Клини, К. Гьоделем и Е. Постом. Предложенные ими машина Тюринга, машина Поста, частично рекурсивные функции и лямбда-вычисления Черча були эквивалентными формализмами алгоритма. Сформулированные ими тезисы (Поста и Черча-Тюринга) постулировали эквивалентность предложенных ими формальных систем и интуитивного понятия алгоритма. Важным развитием этих работ стало формулирование и доказательство алгоритмически нерешаемых проблем. В 1950-ые — годы существенных вклад в теорию алгоритмов сделали работы
А. М. Колмогорова и А. А. Маркова (младшего), а в 1970-х годах в теории алгоритмов плодотворно работал Ю. В. Матиясевич, в частности над решением проблем Гильберта.
Предложенное А. Марковым понятие “нормального алгоритма“ является величичайшим вкладом в мировую науку, а А. Колмогорову принадлежит приоритет в определении общего понятия алгоритма и созданияя теории сложностиі конструктивных объектов.
В 1960-70-ые годы сформировались такие направления в теории алгоритмов:
- Класическая теория алгоритмов (изложение задания в терминах формальных языков, понятие задачи решения, введение классов сложности, формулирование в 1965 году Эдмондсом проблемы P=NP, открытие класса NP-полных задач и их исследование)[1].
- Теория ассимптотического анализа алгоритмов (понятие сложности и трудоемкости алгоритма, критерии оценки алгоритмов, методы получения ассимптотических оценок, а именно для рекурсивных алгоритмов, ассимптотический анализ трудоемкости или время выполнения), в розвитии которой сделали существенный вклад Кнут, Ахо, Хопкрофт, Ульман [2,4].
- Теория практичного анализа вычислительных алгоритмов (получение явных функций трудоемкости, практические критерии качества алгоритмов, методика выбора рациональних алгоритмов), основополагающими работами в этом направлении, очевидно, следует считать фундаментальные труды [1,2].
С тех пор многие ученые приложились к развитию теории алгоритмов. Необходимо отметить также весомый вклад в теорию алгоритмов, сделанный Д. Кнутом, A. Ахо и Дж. Ульманом. Необходимо вспомнить и другие издания книги “Алгоритмы: построение и анализ“ Томаса Х. Кормена, и труды Чарльза І. Лейзерсона, Рональда Л. Ривеста, Клиффорда Штайна.
Ученые, которые упорядочили теорию алгоритмов, рано или поздно сталкивались с тем, что необходимо определить объект исследований. Оказалось, что все разнообразные определения, поданные ими относительно алгоритма, являются эквивалентными понятиями, и чудесным научным результатом есть доказательство эквивалентности этих формальных определений в содержании их равнозначности. Приводя все определения, как говорят математики, “к общему знаменателю“, можно дать общее определение алгоритма:
Алгоритм – способ превращения информации по правилам, сформулированным определенным языком.
Несмотря на усилия исследователей, отсутствует единственно исчерпывающее строгое определение понятия алгоритма. Все они являются интуитивными, точно также и те, котрые приведены выше. Интуитивно говоря, чтобы получить решение какой-либо задачи необходимо выполнить действия по строго определенному формальному предписанию. Это формальное предписание и есть алгоритмом.
В общем случае понятно, что алгоритм – это детерминированная процедура, которую можно применить к любому элементу определенного класса символьных входов и которая для каждого такого входа выдает через конечное число действий (шагов) соответствующий результат свого действия. Пусть D — область (множество) исходных данных задачи, а R — множество возможных результатов, тогда мы можем говорить, что алгоритм А осуществляет отображение А : D → R.
Любой алгоритм должен иметь такие основные особенности или характеристики:
Определенность (однозначность) — каждая команда алгоритма однозначно определяет действия исполнителя и не допускает двойного толкования.
Дискретность – возможность разбиение алгоритма на конечное количество этапов, причем результаты предыдущего этапа есть входными для последующего.
Массовость – алгоритм может быть использован для решения целого класса задач одного типа, для которых он создан.
Понятность – алгоритм должен быть понятным конкретному исполнителю, который должен исполнить каждую команду алгоритма в строгом соответствии с предназначением.
Результативность (сходимость) – исполнение алгоритма должно оканчиваться результатом или информацией о том, что не может быть полученным результат.
Именно этим характеристикам часто дается интуитивное определение алгоритма как конечной однозначно определенной последовательности операций, формальное выполнение которой приводит к решению поставленой задачи за конечной число шагов.
Пример 10.1. Рассмотрим алгоритм Эвклида нахождение наибольшего общего делителя двух натуральных чисел a и в ( НСД (а, в)). Этот алгоритм перерабатывает слова вида (а,в) в алфавите, который состоит из 10 цифр, “ (“ и“)“, знака пунктуации “ , “, в слова того же самого алфавита (результатом будет слово из цифр). Конечная система правил, которая определяет этот алгоритм, будет складываться из правила деления, определение остатка от деления и правила определенности , когда алгоритм заканчивает работу и выдает результат.
Пример 10.2. Рассмотрим процес приготовления блюда быстрого питания : 1. Высыпать в пустую посуду содержимое пакетика. 2. Влить в емкость 200 мл горячей воды. 3. Тщательно перемешать. Чтоб выполнить конечную систему правил по этому “алгоритму», необходимо проделать чисто механические действия.
Хотя последний пример не является алгоритмом в том смысле, который мы определили. Поскольку он не отвечает всем требованиям его характеристик, дадим ему определение “почти“ алгоритм, точно также как и медицинским рецептам. Подумайте почему? Именно такое разделение.
Понятно, что алгоритм как сущность пришел к фундаментальным достижениям человечества из математики, а в современности получил статус центральной оси программирования и информатики в целом. По своей природе алгоритм – это интелектуальный продукт, который является найденным его создателем последовательностью действий над входной информацией, строгое выполнение которых приведет к желаемому или не желаемому результату. Алгоритм существует тогда и только тогда (или начинает существовать), когда существует в тоже самое время какой-то объект (чаще всего математическая его модель) или проблема, для решения которой он и создан.
По назначению алгоритм с входными данными сопоставляет выходные данные и в этом он чем-то схож с позиций математики на обычную функцию, а с позиций информатики — на способ преобразования информации. Однако главной особенностью алгоритма есть то, что он содержит описание именно лействий, как это делать. Функция может буть задана неявно, а алгоритм — нет. Алгоритм описывает одним из возможных способов своего представления( см. п.10.2), что необходимо сделать с исходными данными, чтобы получить результат.
Данное выше толкование алгоритма нельзя считать строгим в научном смысле, так как не совсем понятно, что такое “последовательность действий, которое обеспечивает получение необходимого результата“. Поэтому обычно формулируют несколько общих свойств(характеристик) алгоритмов, что разрешает отличать алгоритмы от других подобных инструкций (см. п.10.1). Однако даже знание этих свойств не дает возможность определить, являются ли данные инструкции алгоритмом, или нет. Наверно, одним из определяющих для решения этой проблемы, является свойство однозначности выполнения каждой команды, данной в инструкции. Если результат выполнения каждого шага инструкции происходит однозначно и независимо от исполнителя, то эти инструкции составляют именно алгоритм.
10.2. Способы задания алгоритмов
Если взять за основу, что алгоритмы с позиции математики являются строгими правилами решения какой-либо задачи, а с позиции информатики являются центральным звеном в цепи модель-алгоритм-программа (см. выше), то правильность алгоритмов есть залогом надежного функционирования компьютерных программ, достоверности результатов в решении научных и жизненных проблем и вообще адекватного мировосприятия. Короткую простую программу можно написать непосредственно исходя из постановки задания без предварительной разработки алгоритма. Однако реальную программу так же трудно создать без алгоритма, как трудно изготовить достаточно сложную деталь без чертежа.
В этом смысле, кроме правильности самих алгоритмов по сути решение самой проблеми, необходимо иметь удобное и понятное их представление для практического применения конкретному исполнителю. При задании алгоритма необходимо позаботиться про то, чтобы алгоритм воспринимался всеми исполнителями однозначно и точно, чтобы его можно было выполнить при любых допустимых исходных условиях, и чтобы необходимый результат был получен за приемлемое время. Очевидно, что предписание “Пойди туда, не знаю куда, принеси то, не знаю что“ алгоритмом не является.
Существует несколько методов записи или представления алгоритмов. Выбор метода зависит от исполнителя и представленных разработчиком вари анто в представления алгоритмов.
Першый способ задания алгоритмов — это словесно-формульный (описание осуществляется в словесной форме с использование математических или других формул). Он описывает выполнение действий алгоритма в определенной последовательности с помощью слов и предложений естественного языка. Форма изложения произвольная и устанавливается разработчиком. В математике наличие формул позволяет решить задачу, даже “не используя слов“.
Пример 10.3. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел (алгоритм Эвклида).
Решение. Алгоритм может быть представлен таким образом:
1. Возьмите два числа.
2. Если числа однаковые, то взять любое из них как ответ и остановиться, иначе продолжить выполнение алгоритма.
3. Определить наибольшее число.
4. Заменить большее из чисел разницей большого от меншого числа.
5. Повторити алгоритм с шага 2.
Другой способ задания алгоритмов — это представление алгоритма в виде таблиць, формул, схем, рисунков и т.д. Например, всех нас учили в детстком саду правилам поведения на дороге. И некоторые дети, очевидно, лучше воспринимают этот алгоритм, в виде схематического рисунка. Смотря на них, ребенок, а потом и взрослый человек, воспроизводять ту линию поведения, которую им предлагают.
Третий способ задания алгоритмов — это запись алгоритмов с поможью блок-схемы. Этот метод был предложен в информатике для наглядности представления алгоритма с помощью набора специальных блоков. Блок-схема – это такое графическое представление алгоритма, при котором решение задачи изображается в виде разных геометрических фигур, в середине которых записаны тексты, что вместе с формой фигуры объясняет и действия, которое необходимо выполнить, и взаимосвязи между ними.
Схема алгоритма четко определяет последовательность действий, заданных этим алгоритмом. Согласно характеристике дискретности схема может представлять собой алгоритм из разных ступеней детализации. При этом важно более точно и наглядно изображать управляющие структуры алгоритма, которые показывают логику перехода от одного действия к другому. Однако требования к графическому исполнению схем вызывают предубеждение некоторых программистов, представляются основным недостатком схем и заставляют искать новые способы записи алгоритмов.
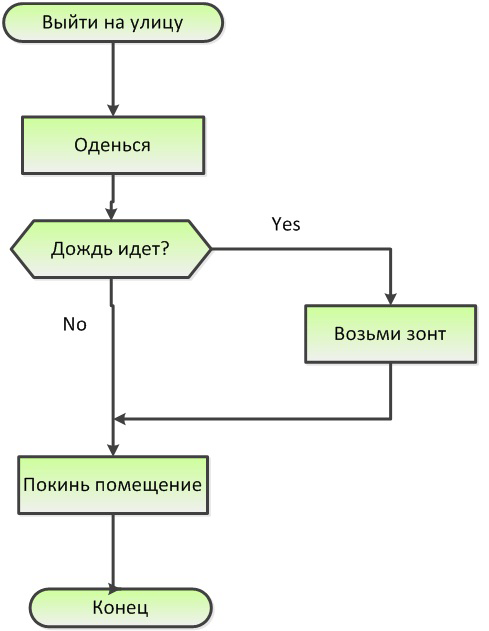
Пример 10.4. Используя необходимые для представления блоки, можно представить, например, алгоритм «Выхода на улицу» в таком виде:
Четвертый способ задания алгоритмов – это запись алгоритма учебным алгоритмическим языком (псевдокодом).
Псевдокодом называется система правил записи алгоритма, с использованием набора определенных конструкций, для описания управляющих действий. Псевдокод является основным способом представления алгоритмов для теоретических исследований в теории алгоритмов. Именно на этих конструкциях отрабатывается, например, нахождение асимптотических оценок алгоритмов.
Единого, или формального, определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций. В отличии от стандартизации синтаксиса языков программирования, на синтаксис псевдокода обычно не устанавливается стандартов, поскольку последний непосредственно не компилируется в исполнительную программу. Поэтому можно сказать, что обычно автор каждой публикации применяет свой оригинальный псевдокод, заимствуя нужные ему конструкции из любого языка программирования. Их использование можно объяснить как индивидуальными симпатиями автора, так и распространенностью на момент написания публикации. В случае русскоязычных публикаций как псевдокод, часто используется перевод ключевых слов языков программирования с английського на русский.
В ряде случаев псевдокодом называють систему команд абстрактной машины, например, P-код, псевдокод придуманной машины MIX и т. д. В отличии от псевдокода неформального характера такой псевдокод уже строго формализованый и может быть транслирован в работающую программу при наличии программы-эмулятора данной гипотетической машины.
Известны прогнозы, которые утверждают, что дальнейшее развитие языков программирования пойдет путем их сближения с псевдокодом, что на конечном этапе позволит осуществлять программирование на естественных языках.
Пример 10.5. Записать на псевдокоде алгоритм Евклида – нахождение наибольшего общего делителя двух чисел.
Вы, наверно, заметили, что этот вариант алгоритма отличается от алгоритма, представленного во время решения примера 10.1. На самом деле существует несколько вариантов написания алгоритма Евклида, в данном случае записан в псевдокоде рекурсивный вариант.
Пятый способ, максимально приближен к компьютеру, задания алгоритмов — это языки программирования. Дело в том, что наиболее часто на практике исполнителем созданного человеком алгоритма является машина, и поэтому он должен быть написан языком, понятным для компьютера, т.е. языком программирования. Язык программирования — это знаковая система, предназначена для описания процессов решения заданий и их реализации на ЭВМ. Реализация обозначает, что описания могуть быть введены в ЭВМ и однозначно ею поняты. К языкам программирования принадлежат языки команд или машинные языки и языки высокого уровня.
Источник