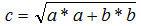Способы задачи алгоритма с примерами

Способы задания алгоритма — Алгоритмы — Краткий теоретический справочник

Алгоритм — заранее заданное возможному исполнителю точное предписание совершить определённую последовательность действий для получения решения задачи за конечное число шагов.

4.1. Способы задания алгоритма

На практике наиболее распространены следующие способы задания алгоритмов:

— словесный (запись на естественном языке);

— графический (изображения из графических символов);

— псевдокод (полуформализованное описание алгоритмов на условном алгоритмическом языке, включающее в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);

— программный (тексты на языках программирования).

Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задаётся в произвольном изложении на естественном языке.

Пример. Запишите алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел (алгоритм Евклида).

Алгоритм может быть следующим:

1) Задать два числа.

2) Если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма.

3) Определить большее из чисел.

4) Заменить большее из чисел разностью большего и меньшего из чисел.

5) Повторить алгоритм с шага 2.

Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи.

При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Такое графическое представление называется схемой алгоритма, или блок-схемой. В блок-схеме каждому типу действий соответствует геометрическая фигура, представленная в виде блочного символа. В таблице приведены наиболее часто употребляемые символы.

Начало, конец алгоритма, входи выход в подпрограмму

Вычислительное действие или последовательность действий

Вычисления по подпрограмме

Ввод-вывод в общем виде

Блок «процесс» применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.

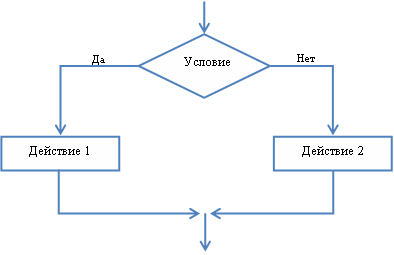
Блок «решение» используется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.

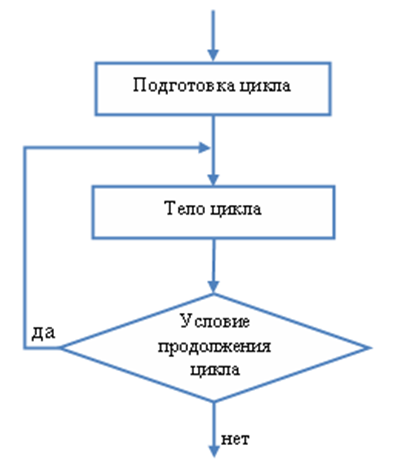
Блок «модификация» используется для организации циклических конструкций. Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.

Блок «предопределённый процесс» используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.

Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.

В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам. В псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых однозначно определён. Например, алгоритмы на алгоритмическом языке записываются с помощью служебных слов, представленных в таблице 1.8.

Таблица 1.8. Служебные слова алгоритмического языка.

Источник

Алгоритмы

Алгоритмы. Разработка алгоритма решения задачи

Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.

Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.

При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.

В процессе разработки алгоритма решения задачи можно выделить следующие этапы:

• Этап 1 . Математическое описание решения задачи.
• Этап 2 . Определение входных и выходных данных.
• Этап 3 . Разработка алгоритма решения задачи.

Базовые алгоритмические конструкции

В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:

• следование (линейный алгоритм);
• ветвление (разветвляющийся алгоритм);
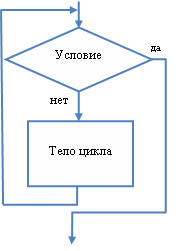
• цикл-пока (циклический алгоритм).

Линейные алгоритмы

Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.

Пример

ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.

На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:

Этап 1. Математическое описание решения задачи.

Математическим решением задачи является известная формула:

,

где с-длина гипотенузы, a, b – длины катетов.

Этап 2. Определение входных и выходных данных.

Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.

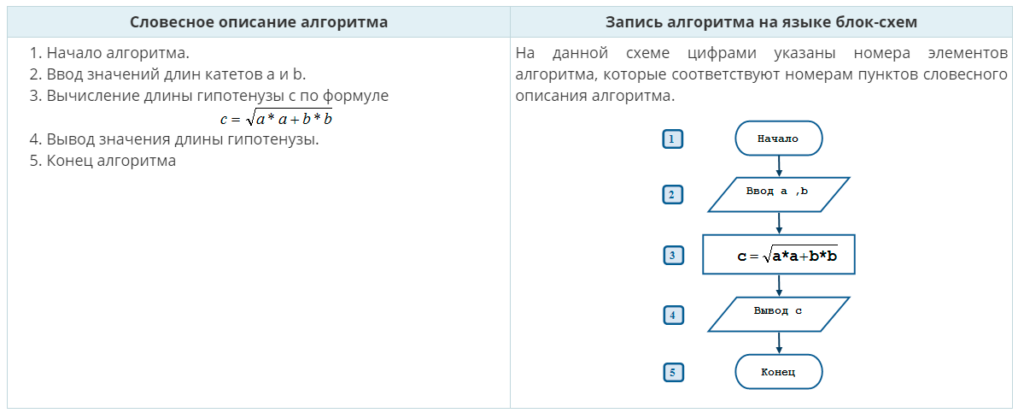
Этап 3. Разработка алгоритма решения задачи.

На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма.

Разветвляющиеся алгоритмы

Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.

Пример

ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.

Этап 1. Математическое описание решения задачи.

Из курса математики известно, если x > y, то наибольшее число x, если x y, то переход к шагу 6, иначе к шагу 7.

В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма

В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:

• первая: это элементы 1, 2, 3, 4, 8.
• вторая: это элементы 1, 2, 3, 5, 6, 8
• третья: это элементы 1, 2, 3, 5, 7, 8.

Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.

Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.

Циклические алгоритмы

Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.

Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.

При разработке алгоритма циклической структуры выделяют следующие понятия:

• параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
• начальное и конечное значения параметров цикла;
• шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.

Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.

В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:

• начальные значения цикла;
• конечные значения цикла;
• шаг цикла.

В тело цикла входят:

• многократно повторяющиеся действия для вычисления искомых величин;
• подготовка следующего значения параметра цикла;
• подготовка других значений, необходимых для повторного выполнения действий в теле цикла.

В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.

Пример

ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.

Этап 1. Математическое описание решения задачи.

Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:

где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.

Этап 2. Определение входных и выходных данных.

Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.

Выходные данные – значение суммы членов последовательности натуральных чисел.

Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.

Подготовка цикла заключается в задании начального и конечного значений параметра цикла.

• начальное значение параметра цикла равно 1,
• конечное значение параметра цикла равно n,
• шаг цикла равен 1.

Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.

Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:

Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.

Этап 3. Разработка алгоритма решения задачи.

Введем обозначения: S – сумма последовательности, i – значение натурального числа.

Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.

Источник

Задачи на алгоритмы

Мы уже рассказывали про алгоритмы, их виды и свойства. В этой статье поговорим о том, как составить алгоритм решения какой-нибудь задачи, что и в какой последовательности следует написать.

При решении задач на алгоритмы немаловажным является умение использовать язык блок-схем. Процесс решения одной и той же задачи можно реализовать посредством применения алгоритмов разных классов, поэтому результат может отличаться и по времени счета, и по объему вычислений, и по сложности. Записывая алгоритмическую последовательность с помощью составления блок-схем, вы сможете сравнить решения, выбрав самый лучший algorithm. Также появляется возможность упростить способ решения, найти и устранить ошибку.

Можно ли отказаться от языка блок-схем при описании алгоритма и сразу составить его на языке программирования? Можно, однако существует риск выбора неоптимального решения и существенных потерь времени. Именно поэтому при данной постановке вопроса рекомендуется сначала составлять способ решения задачи путем создания блок-схемы, а уже потом переводить алгоритм на нужный язык программирования.

Когда речь идет о задаче высокого класса сложности, не обойтись без пошаговой реализации. Сначала продумывают общую структуру алгоритмической последовательности, то есть детальная проработка отдельных частей здесь не требуется. Модули, которые далее потребуют более детального рассмотрения, обводят пунктиром, чтобы потом продумать и детализировать.

В решении задачи на алгоритмы выделяют ряд этапов:

1. Математическое описание.
2. Определение входных/выходных данных.
3. Разработка алгоритма по решению поставленной задачи.

Алгоритмические конструкции базовых классов

В теории программирования считают, что для того, чтобы составить запись любого, даже самого сложного алгори тма, хватит 3-х базовых структур. Речь идет о следующих алгоритмах:

• линейного класса;
• ветвления (речь идет о разветвляющихся алгоритмах);
• циклического класса.

Алгоритмы линейного класса

Образуются из последовательности действий, которые следуют одно за другим. К примеру, чтобы определить площадь прямоугольника, надо сначала задать длину 1-й стороны, потом — 2-й стороны, ну а в конце уже можно решать пример по формуле нахождения площади.

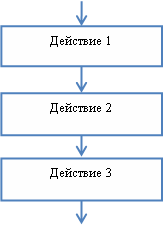Алгоритм линейного класса

В качестве примера возьмем задание с разработкой алгоритма по вычислению гипотенузы прямоугольного треугольника, зная длины катетов a и b. Вспоминаем вышеописанные этапы разработки:

1. Математическое описание.

Математически задача решается по следующей формуле:

Здесь c является длиной гипотенузы, a, b – длинами катетов.

2. Определяем входные/выходные данные.

Входные данные — значения катетов a и b. Выходные — длина гипотенузы c.

3. Разработка алгоритма.

Алгоритмы ветвления

В таких алгоритмических последовательностях всегда существует какое-нибудь условие. В зависимости от того, соблюдается это условие либо нет, происходит выполнение той либо иной последовательности действий.

Для примера возьмем задание, постановка которого связана с разработкой алгоритма по вычислению наибольшего числа из 2-х чисел: x и y.

1. Математическое описание.

Из первых классов математики мы знаем, что когда x > y, то x больше y и наоборот, что является очевидными вещами. И если x = y, то числа равны.

2. Определяем входные/выходные данные.

Входные данные — это значения x и y. Выходными данными являются:

• самое большое число;
• любое из чисел в том случае, если они равны.

Таким образом, чтобы решить эту задачу на алгоритмы, надо знать значения переменных x и y.

3. Разработка.

В вышеуказанной схеме цифрами отмечены номера алгоритмических элементов, соответствующие номерам шагов словесного описания. Здесь есть 3 ветви решения:

Алгоритмы циклического класса

В алгоритмах циклического класса некоторая часть действий из задания повторяется до тех пор, пока не нарушится заранее определенное условие. Выполнение условия проверяется в начале. Совокупность операций, которые выполняются многократно, — это тело цикла.

В алгоритмических последовательностях этого класса выделяют ряд понятий:

• параметр цикла (с изменением этой величины связано многократное выполнение цикла);
• начальное и конечное значения циклических параметров;
• шаг цикла (речь идет о значении, на которое меняется параметр при каждом повторе).

Работу циклов организуют по специальным правилам. Алгоритмическая последовательность циклического класса включает в себя и подготовку, и тело, и условия продолжения работы.

В подготовку входят действия, которые связаны с заданием исходных значений:

• начальные значения;
• конечные значения;
• шаг.

В тело цикла входят:

• многократно повторяющиеся операции по вычислению искомых величин;
• подготовка последующего значения параметра;
• подготовка иных значений, нужных для повторного выполнения действий непосредственно в теле.

В условии продолжения цикла определяют допустимость выполнения повторяемых операций. Когда циклический параметр равен либо превышает конечное значение, выполнение прекращается.

Рассмотрим задание, постановка которого связана с разработкой алгоритма вычисления суммы натуральных чисел в диапазоне от 1 до 100.

1. Математическое описание.

Сначала следует обозначить сумму натуральных чисел буквой S. В результате формулу вычисления суммы чисел от 1 до 100 можно записать следующим образом:

Здесь Xi является натуральным числом X c номером i. Этот номер меняется от 1 до n. А n=100 обозначает общее кол-во натуральных чисел.

2. Определяем входные/выходные данные.

Входные данные — это натуральные числа: 1, 2, 3, …, 99, 100.

Выходные данные представляют собой значение суммы членов последовательности натуральных чисел.

Относительно параметра цикла — речь идет о величине, определяющей число циклических повторений. В нашем задании i представляет собой номер натурального числа.

Подготовка цикла — задание начального и конечного значений циклического параметра. Тут надо пояснить следующее:

• начальное значение циклического параметра равняется единице,
• конечное значение — n,
• шаг равен 1.

Чтобы обеспечить корректность суммирования, надо, чтобы начальное значение суммы предварительно равнялось нулю.

Тело цикла. В теле станут выполняться как накопление значения суммы, так и вычисление последующего значения циклического параметра по формулам ниже:

Циклическое повторение должно осуществляться до тех пор, пока не добавится последний член последовательности натуральных чисел, то есть до тех пор, пока циклический параметр будет меньше либо равен окончательному значению параметра.

3. Разработка.

Вводим следующие обозначения: S – это сумма последовательности, i – это значение натурального числа.

Начальное циклическое значение i=1, конечное — i =100, шаг равен 1.

Источник

Вам также может понравиться

Ясень семена способ распространения

Ясень обыкновенный Fraxinus excelsior – так в ботанической

Ярлыки способы создания ярлыков ос windows

Создаем ярлыки на рабочем столе Windows Создаем ярлыки

Японское удобрение фуджима способ применения

Удобрения Фуджима Знаете потрясающее удобрение, палочка

Японский чай способ заварки

Технология заваривания японского чая Известно, что