Способы взаимодействия тел между собой

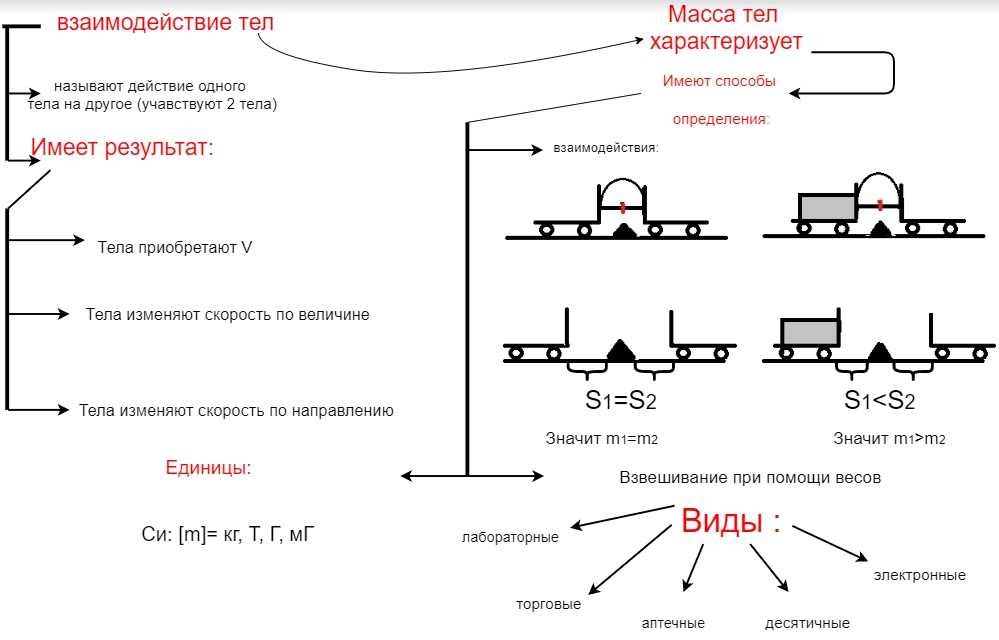
Конспект по теме взаимодействие тел

1. Понятие взаимодействия тел

Взаимодействием тел называют действие одного тела на другое.

Во взаимодействии участвуют два тела.

2. Примеры взаимодействия тел

Например: ракетка ударяет по шарику, он начинает двигаться. Футболист ногой ударил по мячу. Мяч приходит в движение. Сталкиваются две тележки. Которые начинают двигаться в противоположные стороны. Сосуд с водой. На поверхности воды лежит кусочек пробки с иглой. Поднесем магнит. Иголка с пробкой начинают двигаться в сторону магнита. Мальчик прыгает с лодки на берег. Лодка движется в противоположенную сторону.

3. Результат взаимодействия тел

Взаимодействие имеет результат:

1. Тела приобретают скорость. (Футболист ногой ударил по мячу. Мяч приходит в движение).
2. Тела изменяют скорость по величине. (Движется шайба по льду с какой-то скоростью. Хоккеист ударяет по шайбе с большей силой, скорость увеличивается).
3. Тела изменяют скорость по направлению. (Спортсмен бросил мяч в стену. Ударившись о нее, он изменяет направление).

4. Понятие массы тела

Масса тела и взаимодействие связаны между собой. То есть масса это мера взаимодействия тел. Пример: Земля взаимодействует с Луной. Способом взаимодействия определили ее массу.

5. Способы определения массы тела

Существуют способы определение массы: первый способ взаимодействие. Второй способ взвешивание.

5.1. Взаимодействие тела

Если взять две тележки одинаковой массы. Между тележками установить плоскую изогнутую пружину. Которая связана нитью. Если нить пережечь. То обе тележки отъедут на одинаковое расстояние. Делаем вывод: если тележки отъехали на одинаковое расстояние. Значит и массы этих тележек одинаковые. Если взять две тележки одну нагруженную, а другую пустую. И привести в соприкосновение при помощи упругой пружины. То после пережигания нити тележка, которая нагружена, отъехала на меньшее расстояние. Обладает большей массой. А тележка, которая отъедет на большее расстояние. Обладает меньшей массой.

5.2. Взвешивание при помощи весов

Второй способ определения массы взвешивание. Первое понятие взвешивания дается в школе. С помощью рычажных лабораторных весов. Учащиеся знакомятся с правилами взвешивания:

1. Уравновесить весы при помощи кусочков бумаги.
2. На чашу в которой нет бумаги кладут разновесы.
3. На другую чашу кладут взвешиваемое тело.
4. Весы уравновешены тогда, когда стрелочка отклоняется влево и вправо на одинаковый угол.

5.3. Виды весов

Весы бывают разных видов: лабораторные весы, торговые, аптечные, десятичные, электронные.

6. Единицы массы

Массу измеряют в кГ, Г, мГ, ц, Т. В системе СИ главной единицей, является кГ.

7. Понятие эталона массы

В городе Севра близ Парижа, находится музей. В котором хранятся эталоны масс, размеров тел. 1 кг представляет из себя цилиндр изготовленный из платины и иридия. Эти эталоны хранятся под несколькими стеклянными колпаками. Чтобы их масса не изменилась. Копии эталонов масс приобретают все страны мира. Чтобы торговля была равноценной.

Источник

Взаимодействия тел в физике

Содержание:

Взаимодействие тела – это действие, которое взаимно. Все тела способны между собой взаимодействовать при помощи механического движения, инерции, силы, плотности вещества и, собственно, взаимодействия тел.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Взаимодействия тел

Взаимодействие тел — это воздействие тел друг на друга. Тела могут взаимодействовать при помощи механического воздействия, инерции, свойств вещества (плотности), электричества и прочих факторов.

Третий закон Ньютона

Сила в механике характеризует действие одного тела на другое. Когда мы говорим, например, что на тело действует сила, то это значит, что на это тело действует какое-то другое тело. Но во всех случаях, когда одно тело действует на другое, имеется не одностороннее действие, а взаимодействие тел. Это значит, что если одно тело действует на другое, то это другое тело действует на первое.

Проверить только что высказанное утверждение можно на опытах.

Рис. 104. Динамометры показывают одну и ту же величину силы.

На рисунке 104 изображён опыт с двумя динамометрами, соединёнными друг с другом; за кольцо одного динамометра тянут в одну сторону, за кольцо другого—в противоположную сторону. Оба динамометра показывают одну и ту же величину силы. Следовательно, силы и равны по величине и противоположны по направлению.

Сила приложена к одному динамометру, а сила — к другому. Опыт показывает, что растянуть пружину первого динамометра до какого-нибудь деления можно только в том случае, когда и пружина второго динамометра растянута на то же деление.

Рассмотрим ещё случай, когда тела взаимодействуют, находясь на некотором расстоянии друг от друга, не прикасаясь друг к другу; так взаимодействуют электрически заряженные тела и магниты.

Положим на одну тележку магнит, а на другую—кусок железа (рис. 105).

Рис. 105. Динамометры показывают одну и ту же величину силы.

Сзади тележек прикрепим динамометры. Вследствие притяжения между магнитом и железом тележки будут двигаться навстречу друг другу, растягивая при этом пружины динамометров. Когда же они остановятся, то оба динамометра покажут одну и ту же величину силы. На основании этого опыта мы можем сказать, что с какой силой магнит притягивает железо, с такой же силой (по величине) железо притягивает магнит.

Мы рассмотрели случаи взаимодействия покоящихся тел. Рассмотрим теперь взаимодействие движущихся тел.

Рис. 106. Пример взаимодействия движущихся тел.

На рисунке 106 изображены два мальчика, стоящие на тележках. В руках у них верёвка. Когда мальчики натянут верёвку, то оба они вместе с тележками начнут двигаться навстречу друг другу. Силы, которые при этом приложены к мальчикам,оказываются всегда равными и противоположно-направленными, независимо от того, как мальчики натягивают верёвку. Действительно, измерив пути, пройденные тележками, и время движения их, можно убедиться, что ускорения и движения тележек с мальчиками обратно пропорциональны движущимся массам и м т е. или Но и

Значит, по величине причём не следует забывать, что сила приложена к одной тележке, a —к другой Направлены эти силы в противоположные стороны. Учитывая, противоположные направления взаимодействующих сил и равенство (1) надо написать следующим образом:

Итак, во всех случаях силы, с которыми два тела действуют друг на друга, равны по величине и противоположны по направлению.

Если одну из этих сил назвать действующей силой, то другая будет противодействующей.

Такое разделение сил на действующие и противодействующие является условным; от нас зависит, какую из этих сил назвать действующей, какую противодействующей.

Сформулированный выше закон равенства действия и противодействия открыт был Ньютоном и положен им в основу динамики в качестве третьего закона движения.

Из третьего закона следует, что не только Земля притягивает, например, камень, но и камень притягивает к себе Землю с силой, равной весу камня. В результате этого взаимодействия оба тела — Земля и камень—движутся навстречу друг другу (относительно, например, неподвижных звёзд) с ускорениями, обратно пропорциональными их массам.

Так как масса Земли во много-много раз больше массы любого камня, то практически ускорение движения её по направлению к камню равно нулю. Камень же движется по направлению к Земле (падает) с ускорением

При ходьбе мы отталкиваемся ногами от Земли. Земля толкает нас в противоположную сторону. Так как масса Земли велика по сравнению с массой нашего тела, то практически Земля остаётся неподвижной, мы же движемся с некоторой, скоростью. Ноги человека и животных, ведущие колёса автомобиля и паровоза при движении отталкиваются от Земли, гребной винт парохода—от воды, птица и винт самолёта при полёте—от воздуха и т. п. Во всех таких случаях отталкивающее и отталкиваемое тела начинают двигаться в противоположных направлениях с ускорениями, обратно пропорциональными их массам.

Чтобы правильно применять третий закон Ньютона, не следует забывать, что силы действия и противодействия, о которых говорится в этом законе, всегда равны и противоположно направлены, но никогда друг друга не уравновешивают, так как приложены к разным телам.

Если лошадь везёт телегу, то это не значит, что сила, с которой она тянет телегу, больше силы, с которой телега тянет лошадь в противоположную сторону. Силы эти равны по величине. Но ни лошадь, ни телега, вследствие одного только взаимодействия друг с другом, не могут прийти в движение обе в одном и то.м же направлении.

Для этого необходима третья сила, приложенная одновременно и к лошади, и к телеге. Такая сила возникает при взаимодействии лошади с Землёй. Лошадь подковами отталкивает Землю в одну сторону, а Земля толкает лошадь с телегой в другую.

Точно так же двигатель автомобиля, вращая колёса автомобиля, не сдвинет его с места, если отсутствует достаточное сцепление колёс автомобиля с полотном дороги (§ 38).

Сила тяги

Согласно третьему закону Ньютона, силы взаимодействия между двумя телами равны по величине и противоположны по направлению. Эти силы не могут привести в движение оба взаимодействующих тела в одном и том же направлении. Например, одни лишь силы взаимодействия между паровозом и вагонами не могут привести поезд в движение. Для этого необходима третья сила. Такой третьей силой, как уже указывалась (§ 38), является сила трения между ведущими колёсами паровоза и рельсами. Вопрос этот очень хорошо изложен в книге нашего замечательного учёного В. Л. Кирпичёва «Беседы о механике». Выдержка из этой книги приводится:

«Давление пара в паровой машине представляет внутреннюю силу и не может вызвать перемещение центра тяжести поезда. Это подтверждается опытом, который неоднократно делали с паровозами: паровоз подвешивают на цепях и, растопив котёл, пускают машину в ход.

Оказывается, что вследствие хода поршня взад и вперёд получаются лишь небольшие качания всей остальной массы в обратном направлении, а центр тяжести паровоза остаётся неподвижным.

Когда паровоз поставлен на рельсы и машина его пущена в ход, то между его ведущими колёсами и рельсами возникает трение, которое и есть горизонтальная сила, необходимая для движения паровоза с поездом. Явление это состоит в следующем. При вращении колеса, стоящего на рельсе (рис. 107, а), точка А стремится скользить по гельсу по направлению стрелки Я, во этому мешает трение между колесом и рельсом; направление силы трения показано оперённой стрелкой.

Колесо своими неровностями и шероховатостями упирается в рельс и испытывает от рельса обратное давление. Эти шероховатости колеса и рельса представляют как бы миниатюрные зубцы (рис. 107, б), между которыми происходит упор и получается давление. Вот это обратное давление, т. е. трение, передающееся от рельса на колесе, и есть та внешняя сила, которая перемещает центр тяжести паровоза. Она должна преодолеть сопротивление состава вагонов, прицепленных к паровозу, т. е. должна быть больше этого сопротивления. Поэтому для перемещения поезда требуется значительное трение между ведущими колёсами и рельсом, а трение пропорционально давлению, следовательно, необходимо, чтобы ведущие колёса производили значительное давление на рельс. Другими словами, для того чтобы вести тяжёлый поезд, требуется тяжёлый паровоз.

Всё это относится к ведущим колёсам паровоза, т. е. к тем, на которые действует поршень паровой машины, вращающий их. Та часть веса паровоза, которая передаётся на эти колёса, есть полезный груз: чем он больше, тем, сильнее паровоз, т. е. тем Солее тяжёлый поезд он может вести. Кроме ведущих, в паровозе есть поддерживающие колёса, т. е. не соединённые с паровой машиной. Часть веса паровоза, передающаяся на эти колёса, не приносит никакой пользы, т. е. не увеличивает силу тяги паровоза. Эти колёса не дают движущей силы, а, напротив того, сами приводятся в движение так же, как колёса вагонов. Когда поезд идёт по направлению оперённой стрелки (рис.107), то трение рельсов о колёса вращает их. Это трение на вагонных колёсах или на поддерживающих колёсах паровоза направлено в сторону, противоположную движению; оно представляет внешнюю силу, сопротивляющуюся движению поезда.

Итак, движущая сила паровоза представляет собой силу трения его ведущих колёс о рельсы. Мы увеличиваем эту силу тем, что увеличиваем вес паровоза. Если такое средство недостаточно, то можно прибегнуть к другому, на которое можно смотреть как на увеличение трения. Рельс делают зубчатым, и с ним сцепляется стальное зубчатое колесо, сидящее на оси паровоза, т. е. вместо миниатюрных зубцов, имеющихся вследствие шероховатости колеса и рельса, ставят крупные железные и стальные зубья. Такое устройство применяют в горных паровозах, которые должны подниматься по крутым уклонам.

Обратно, всякое уменьшение трения сейчас же уменьшает силу тяги паровоза; это случается, например, при обледенении рельсов. Сила тяги паровоза также обратилась бы в нуль, если бы мы его поставили не на рельсы, а на катки, свободно вращающиеся на своих осях».

Рассмотрим теперь, как можно рассчитать силу тяги паровоза.

Вес той части паровоза, который приходится на ведущие колёса, называется сцепным весом.

Между ведущими колёсами и рельсами существует, как уже указывалось, сила трения скольжения. Коэффициент трения скольжения стальных бандажей колёс паровоза по стальным рельсам равен примерно г/в. Поэтому сила тяги паровоза составляет одну шестую часть сцепного веса паровоза.

где — сцепной вес.

При скорости движения 20 — 40 сопротивление железнодорожного состава катанию может быть принято равным примерно 1/300. Следовательно, по горизонтальному пути паровоз может тянуть за собой поезд, вес которого в 300 раз превышает силу тяги паровоза, а так как сила тяги паровоза составляет 1/6 сцепного веса паровоза, то вес поезда (включая паровоз) при строгой горизонтальности пути в 50 раз превышает сцепной вес паровоза.
Но даже незначительная крутизна пути сильно уменьшает тягу паровоза. Так, например, при подъёме в полградуса паровоз серии „Э» весом в 80 Т может тянуть поезд весом не более 1500 Т.

У тракторов сила тяги в зависимости от характера пути может составлять от 1/3 до 4/5 веса трактора.

Силой тяги лошади, как и в случае паровоза и трактора, является сила трения между подковами лошади и землёй. Величина силы тяги лошади составляет 0,1 —0,2 её веса. При весе лошади около 400 кГ она может развивать тягу от 40 кГ до 80 кГ. Трение же между колёсами повозки и булыжной мостовой равно примерно 1/20 веса повозки. Следовательно, по горизонтальному пути лошадь может тянуть повозку с грузом, вес которых от 2 до 4 раз больше веса лошади.

Количество движения

Закон сохранения количества движения. Для характеристики движения тел почти одновременно с открытием законов динамики в науку была введена физическая величина, называемая количеством движения.

Количеством движения движущегося тела называется произведение массы тела на его скорость (mv).

Количество движения представляет собой векторную величину, имеющую направление скорости.

При взаимодействии тел количество движения от одного тела может передаваться другому. Взаимодействующие тела обмениваются количеством движения.

Проделаем следующий опыт.

Подвесим два одинаковой массы стальных шарика на нитях так, чтобы нити были параллельны и шарики касались друг друга (рис. 113,а). Отклоним правый шарик на некоторый угол (рис. 113,б) и отпустим его. Ударившись о левый неподвижный шарик, он останавливается, а левый шарик приходит в движение и отклоняется на такой же угол (рис. 113,в).

Рис. 113. К закону сохранения количества движения.

Пусть масса каждого шарика равна m и скорость правого шарика в момент удара v. Так как левый шарик до удара покоился, то общее количество движения обоих шариков было равно mv и направлено справа налево. Но левый шарик после удара отклоняется на такой же угол,а следовательно начинает двигаться с такой же скоростью v, с какой правый шарик двигался в момент, предшествующий удару. Следовательно, общее количество движения обоих шариков непосредственно после удара равно количеству движения до удара. Этот опыт показывает, что при взаимодействии двух тел сумма их количеств движения не меняется.

Этот вывод можно получить теоретически, исходя из второго и третьего законов Ньютона.

На рисунке 114 изображены два шара с массами и движущиеся вдоль прямой в одном направлении со скоростями и

Рис. 114. Два шара движутся в одним направлении с разными скоростями.

Пусть скорость второго шара больше скорости первого, т. е. По истечении некоторого времени второй шар нагонит первый. Когда произойдёт столкновение между шарами, возникнут силы взаимодействия, вследствие чего скорости шаров изменятся. Обозначим скорости шаров после взаимодействия буквами и и буквой t время взаимодействия шаров.

Ускорения и возникшие у них при взаимодействии, определятся из равенств:

По второму закону Ньютона силы, действующие на каждый шар, будут соответственно равняться:

По третьему закону Ньютона силы взаимодействия и равны по величине и противоположны по направлению:

Подставим в равенство (3) значения и из равенств (1) и (2); получим:

Сокращая на t, раскрывая скобки и собирая члены, содержащие скорости, помеченные штрихом, в одну сторону равенства, получим:

Полученное соотношение показывает, что сумма количеств движения взаимодействующих тел не меняется.

В этом состоит один из законов природы —закон сохранения количества движения.

Мы пришли к этому закону из рассмотрения взаимодействия двух тел, но можно было бы показать, что он справедлив для любого числа взаимодействующих тел.

Отдача при выстреле. Реактивные двигатели

Как известно, при стрельбе получается отдача: снаряд движется вперёд, а орудие откатывается назад. Снаряд и орудие — два взаимодействующих тела. Для определения скорости, с которой откатывается орудие, можно применить закон сохранения количества движения. Покажем это на примере.

Какую скорость вследствие отдачи получает орудие при выстреле, если масса орудия 1000 кг, масса снаряда 2,5 кг, а скорость его в момент вылета из ствола орудия ?

Рис. 116. Разрез сигнальной ракеты.

Рис. 116а. Ракета в полёте.

До выстрела снаряд и орудие были в покое, сумма их количеств движения равнялась нулю. По закону сохранения количества движения и после выстрела общее количество движения должно остаться равным нулю. Следовательно, можно написать

Знак минус показывает, что направление скорости орудия противоположно направлению скорости снаряда.

Старинные орудия действительно откатывались при выстреле. При современных же тяжёлых снарядах и огромных их скоростях приходится снабжать орудие специальными механизмами, тормозящими его откатку. К числу таких механизмов относятся воздушные, масляные или пружинные компрессоры.

В современной артиллерии при отдаче откатывается только ствол орудия, лафет же остаётся на месте. Откатывающийся при выстреле ствол сжимает пружину или связанным с ним поршнем давит на жидкость, сжимающую воздух в особом резервуаре. После выстрела сжатая пружина или воздух приводит ствол орудия в прежнее положение. В автоматическом оружии отдача используется для перезарядки.

Отдачу можно использовать и так, что „орудие» при этом получит значительную скорость. Таким образом используется отдача во всех так называемых реактивных двигателях.

Принцип действия реактивного двигателя можно проследить на устройстве обычной сигнальной ракеты.

На рисунке 116 показан разрез такой ракеты. Она состоит из трубки, в нижней части которой имеется смесь пороха с угольной пылью, а в верхней—осветительный состав. Порох зажигается фитилём и благодаря примеси угольной пыли не сразу взрывается, а горит в течение нескольких секунд.

Пороховые газы, являющиеся в данном случае своеобразными „снарядами», выбрасываются с большой скоростью через нижний конец трубки. Сама трубка—„орудие“со всем содержимым—под действием давления пороховых газов получает скорость, направленную вверх (рис. 116а).

Этот же принцип лежит в основе движения снарядов, которыми заряжаются прославившиеся в Великой Отечественной войне гвардейские миномёты „катюши».

В настоящее время имеются самолёты с реактивными двигателями, развивающие скорость в и выше.

Впервые мысль о возможности полёта по принципу ракеты была высказана русским революционером Кибальчичем в 1881 г., незадолго до его казни.

Ракеты для полёта, работающие на жидком топливе, впервые были предложены и разработаны знаменитым русским учёным Циолковским в 1903 г. Циолковским была разработана и теория реактивного движения.

Реактивное действие оказывает не только струя газа, но и струя жидкости. В этом можно убедиться на опыте.

На штативе укрепим воронку с резиновой трубкой. Конец резиновой трубки наденем на изогнутую стеклянную трубку (рис. 117).

Рис. 117. Реакция вытекающей струи.

Закроем изогнутую трубку пробкой и наполним воронку водой. Если теперь, вынув пробку, дать воде возможность вытекать,то резиновая трубка отклонится в сторону, противоположную направлению струи. Одновременное силой давления, выталкивающей воду из трубки, появляется сила, толкающая трубку в противоположную сторону. Эта сила называется реакцией вытекающей струи.

Рис. 118. Сегнерово колесо.

На рисунке 118 изображено так называемое сегнерово колесо, вращающееся вследствие реакции вытекающей струи жидкости. Жидкость, вытекая из трубки, вращает колесо в сторону, противоположную изгибам трубок.

На реактивном действии водяной струи основано устройство мощных водяных
турбин, работающих на Днепрогэсе, на Волховской и на многих других
электростанциях.

Закон всемирного тяготения

С понятием веса человек знакомится очень рано. Упавшая на пол игрушка, ушибленная рука или нога при падении самым наглядным образом знакомят ребёнка с силой тяжести или весом тела.

Под действием притяжения Земли тела падают, давят на опоры или натягивают нити, которые препятствуют им падать. Мельчайший невидимый глазом атом притягивается Землёй так же, как и любой предмет, который мы можем наблюдать. Опыт нам говорит, что все тела, независимо от их размеров, притягиваются Землёй.

Но является ли тяжесть свойством только земных тел, или она присуща всем телам природы? Будет ли иметь вес тело, находясь на Луне или на какой-либо другой планете?

Ответ на эти вопросы содержится в открытом Ньютоном законе всемирного тяготения, согласно которому:

две любые частичка, вещества притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.

Закон этот был открыт Ньютоном на основании изучения движения Луны вокруг Земли и планет вокруг Солнца и распространён им на все тела природы и на все частицы, из которых состоят эти тела.

Рис. 119. Определение гравитационной постоянной (схема).

Согласно закону всемирного тяготения, каждая частица планеты и планета в целом притягиваются Солнцем, Солнце . же притягивается в свою очередь планетой. Луна притягивается Землёй, так же как притягивается любое тело, находящееся на поверхности Земли. Таким образом, вес тел на Земле обусловлен силой тяготения.

С помощью закона всемирного тяготения описываются с огромной степенью точности движения небесных тел, а также предсказываются на много лет вперёд солнечные и лунные затмения, что является основной опытной проверкой этого закона.

Силы притяжения, существующие между телами, с которыми мы встречаемся в нашей практике,очень малы, непосредственно их даже нельзя обнаружить, но с помощью тонких лабораторных опытов их можно измерить. Один из таких способов измерения силы тяготения мы рассмотрим, но прежде выразим закон всемирного тяготения математической формулой.

Обозначим буквой F силу притяжения между массами и находящимися на расстоянии r друг от друга. Тогда:

Буквой (греческая гамма) в этой формуле обозначена величина, численно равная силе, с которой притягиваются два тела с массами по 1 г каждое, находящиеся на расстоянии 1 см одно от другого. Эта величина называется гравитационной постоянной. Её можно определить, например, на следующем опыте.

Два свинцовых шара А и В равного веса (приблизительно 20 кг) подвешены к коромыслу больших равноплечих весов (рис. 119). Третий шар С, вес которого приблизительно в семь раз больше, чем А или В, укреплён на вращающемся столике таким образом, что может устанавливаться в точности под центром шара А или В. Масса каждого шара и расстояние между центрами шаров А и С (или В и С) тщательно измеряются. Если шар С находится под шаром В, то вес шара В увеличивается приблизительно на 0,4 мг; это и будет величина силы Г, с которой шары В и С притягиваются друг к другу.

В формуле (1), таким образом, будут известны все величины, кроме гравитационной постоянной, которую теперь легко вычислить.

На основании многих опытов было установлено численное значение гравитационной постоянной:

(если сила измерена в динах, масса—в граммах, а расстояние—в сантиметрах).

Это значит, что два тела с массами по 1 г, находясь на расстоянии 1 см, притягиваются друг к другу с силой,равной дины.

Масса и вес тела

Существуют два способа взвешивания тел: 1) на пружинных весах и 2) на рычажных весах. Оба эти способа принципиально различны.

Если измерять пружинными весами вес одного и того же тела на различных высотах над поверхностью Земли, то можно заметить, что с увеличением высоты вес тела убывает.

Это уменьшение веса невелико, но важно то, что оно имеется и является одинаковым для всех тел, а именно: при поднятии на каждый километр вес тела убывает приблизительно на 0,0003 своей величины.

Пользуясь пружинными весами, можно обнаружить также, что вес тела изменяется в зависимости и от географической, широты местности: по мере приближения к экватору вес тела убывает. Всякое тело, перенесённое с полюса на экватор, уменьшается в весе приблизительно на 0,005 веса на полюсе.

С помощью пружинных весов мы измеряем силу, с которой тело притягивается Землёй, т. е. вес тела. Таким образом, вес тела не является величиной постоянной: с изменением местоположения тела его вес изменяется.

Но если мы будем взвешивать тело на рычажных весах, то в любом месте мы получим всегда один и тот же результат, так как в этом случае будем определять массу тела. Рассмотрим это подробнее.

Пусть массы двух каких-либо тел и а веса этих тел в одном и том же месте на Земле (g одинаково для обоих тел) и

На основании второго закона Ньютона можно написать, что

Разделив равенства (1) на (2), получим:

Массы тел пропорциональны их весам.

Эталон массы 1 кг в месте его хранения весит 1 кГ, следовательно, численное значение массы какого-либо тела в метрических единицах в месте хранения эталона массы равно численному значению его веса в тех же единицах. В других местах на Земле этого совпадения не будет.

Однако, как видно из сказанного выше, изменение веса с изменением местоположения тела на Земле незначительно; поэтому во многих практических случаях мы можем не считаться с этим изменением. В таких случаях, независимо от местонахождения тела, мы можем принять численное значение его веса, выраженного в единицах метрической системы, равным численному значению его массы в тех же единицах. Так, например, если какое-либо тело весит 100 Г, то и его масса в граммах тоже будет 100 г, и если масса тела 5 т, то его вес тоже 5 Т, и т. д.

В следующей таблице даны характеристики массы и веса.

В метрической системе мер единицы массы и веса имеют одинаковые названия.

Чтобы отличить единицы веса от единиц массы, условились обозначать:

Единицы массы
1 г (грамм массы)
1 кг (килограмм массы)
1 т (тонна массы)

Единицы веса
1 Г (грамм силы)
1 кГ (килограмм силы)
1 Т (тонна силы)

Массы некоторых тел
Атом водорода

Молекула воды
Песчинка
Винтовочная пуля 9,65 г
Автомобиль «Победа» (без нагрузки) 1530 кг
Автомобиль грузовой ЗИС-150 (без нагрузки) 3900 кг
Трактор ДТ-54 5400 кг
Паровоз ФД 120 т
Линкор 25000—50 000 т

Удельный вес и плотность

Удельным весом вещества называется величина, измеряемая отношением веса Р тела, состоящего из этого вещества, к его объёму V.

Обозначив удельный вес буквой d, можем написать:

Из этого определения следует, что удельный вес веще ства численно равен весу единицы объёма тела (предполагается, что тело однородно и состоит целиком из рассматриваемого вещества).

Единицами измерения удельного веса могут быть:

и т. д.

Наряду с величиной удельного веса в физике пользуются величиной плотности вещества.

Плотностью вещества называется величина, измеряемая отношением массы тела к его объёму.

Обозначив плотность буквой D, можем написать:

Плотность вещества численно равна массе вещества, заключённой в единице объёма тела. Например, 1 ртути имеет массу в 13,6 г, следовательно, плотность ртути а в 1 пробки заключена масса всего в 0,24 г, следовательно, её плотность

Ниже приведена таблица плотностей некоторых газообразных, жидких и твердых веществ в или

Газы (при 0° С и давлении 760 мм ртутного столба):
Водород . . . 0,00009 Воздух . . . 0,00129
Гелий . 0,00018 Кислород . . 0,00143
Азот 0,00125

Жидкости:
Эфир этиловый при 20°С . 0,71 Бензин при 15°С . 0,68—0,70
Спирт этиловый безводный при 18°С . 0,79
Керосин при 15°С . 0,79—0,82
Масло растительное . 0,90—0,93 Вода чистая при 4°С . 1
Вода морская при 15°С . 1,02—1,03 Молоко при 15°С . 1,028—1,032

Твёрдые тела
Ель (сухая) . 0,60 Олово . 7,2—7,4
Берёза (сухая) . 0,72 Железо . 7,7—7,8
Дуб (сухой) . 0,80 Латунь . 8,4—8,5
Лёд . 0,9 Медь . 8,8—8,9
Магний . 1,74 Серебро . 10,5
Кирпич . около 1,8 Свинец . 11,4
Алюминий . 2,6—2,7 Золото . 19,3
Стекло . 2,5—2,7 Платина . 21,5
Цинк . 7 Иридий . 22,4

Зная плотность вещества и объём тела, можно определить массу тела:

Принимая во внимание, что P=mg = DVg, подставим это значение веса в выражение удельного веса, получим: d=Dg.

Удельный вес вещества равен произведению плотности вещества на ускорение свободного падения.

Следовательно, соотношение между удельным весом и плотностью такое же, как и между весом тела и его массой. Пользуясь соотношением d = Dg, необходимо, как и во всех случаях, все величины выражать в единицах одной системы единиц.

Определение массы и плотности Земли

По закону всемирного тяготения сила взаимодействия двух тел

Если известна сила F, с которой взаимодействуют два тела, и масса одного из этих тел, то, зная расстояние г между ними, можно определить массу второго тела по формуле:

Тело массой = 1 г притягивается к Земле с силой:

Расстояние между телом и центром Земли составляет приблизительно:

Подставляя числовые значения величин в формулу (1), можем вычислить массу Земли

Так как объём Земли V составляет около то средняя плотность Земли приблизительно равна

Средняя плотность Земли почти вдвое больше средней плотности исследованной части земной коры. Это согласуется с предположением геологов о том, что центральная часть Земли содержит в себе большое количество железа.

Ниже приводятся массы некоторых небесных тел, средние их плотности и ускорения свободного падения на них.

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник