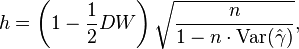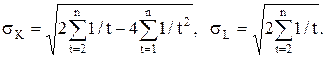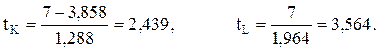Способы выявления тренда временного ряда

Определение тренда временного ряда

Тренд временного ряда— это медленные изменения параметров исследуемого процесса. При изучении тренда решают две задачи:

1) проводят анализ влияния факторов на результирующий показатель (факторный анализ);

2) методом экстраполяции прогнозируют поведение результирующего показателя в следующие моменты времени.

При исследовании тренда применяют методы скользящей средней, сглаживания по нескольким точкам, аналитического выравнивания, частным случаем которого является регрессионный метод, и т.д. Разработка математической модели тренда позволяет на ее основе решать обе задачи: проводить анализ и прогнозировать динамику результирующего показателя. Однако в основе модели должны лежать определенные логические построения и ее (модель) в обязательном порядке необходимо проверить на адекватность. Модель считается адекватной, если коэффициент детерминации (квадрат коэффициента корреляции) больше 0,5.

Сглаживание временного ряда.Цель сглаживания заключается в том, чтобы выделить тренд, т.е. установить основную закономерность ряда, его детерминированной компоненты. Выделение тренда составляет первоочередную задачу стохастического исследования. Чаще всего первым этапом для выделения тренда становится применение метода сглаживания (выравнивания, фильтрации). Один из простейших методов сглаживания — метод скользящей средней.

Модель скользящей средней основана па том, что за сглаженное значение ряда в любой дискретной точке Iпринимают среднее значение в некоторой окрестности с центром в этой точке. При изменении момента времени окрестность скользит вдоль оси ичем и объясняется название модели. Модель позволяет получить для всех точек исходного временного ряда (х()последовательность (г/,), которая является сглаженным рядом исходной последовательности. Скользящие средние могут быть взвешенными и простыми.

Большую точность определения тренда дает метод аналитического сглаживания. При этом динамический (временной) ряд заменяется некоторой его аппроксимацией (приближением). Выравнивание проводится но прямой, если для ряда характерна более или менее постоянная скорость; по параболе, если постоянно ускорение; по экспоненте (показательной кривой), если постоянны темпы роста. Чаще всего (и точнее) тренд получают путем аппроксимации полиномом, причем чем выше степень полинома, тем точнее получается приближение. Вместе с тем, чем выше степень полинома, тем больше вклад сезонной и случайной составляющих в аппроксимацию тренда.

В связи с этим при стохастическом исследовании нужно выбирать такую (минимальную) степень полинома, которая соответствует адекватной математической модели изучаемого процесса.

35. Учет автокорреляции остатков временного ряда. Критерий Дарбина-Уотсона.

Критерий Дарбина—Уотсона (или DW-критерий) — статистический критерий, используемый для тестирования автокорреляции первого порядка элементов исследуемой последовательности. Наиболее часто применяется при анализе временных рядов и остатков регрессионных моделей.

Критерий Дарбина—Уотсона неприменим для моделей авторегрессии, так как он для подобного рода моделей может принимать значение, близкое к двум, даже при наличии автокорелляции в остатках. Для этих целей используется -критерий Дарбина.

-статистика Дарбина применима тогда, когда среди объясняющих регрессоров есть . На первом шаге методом МНК строится регрессия. Затем критерий Дарбина применяется для выявления автокорреляции остатков в модели с распределёнными лагами [2] :

· — число наблюдений в модели;

· — оценка дисперсии коэффициента при лаговой результативной переменной .

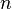
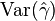
При увеличении объёма выборки распределение -статистики стремится к нормальному с нулевым математическим ожиданием и дисперсией, равной 1. Поэтому гипотеза об отсутствии автокорреляции остатков отвергается, если фактическое значение -статистики оказывается больше, чем критическое значение нормального распределения [3] .

Ограничение данной статистики следует из её формулировки: в формуле присутствует квадратный корень, следовательно, если дисперсия коэффициента при велика, то процедура невыполнима.

36. Сглаживание временных рядов.

Выравнивание временных рядов [time-series smoothing] — выявление основной тенденции развития (временнóго тренда) путем «очистки» временного ряда от искажающих эту тенденцию случайных отклонений. Предполагается, что каждый член ряда состоит из двух компонент: уровня u_t и случайного отклонения от него e_t:

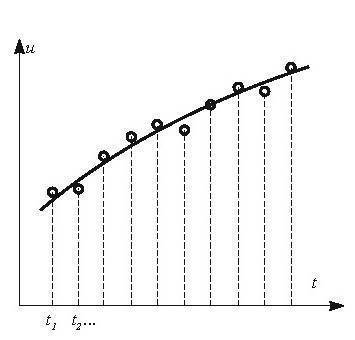
Слагаемое u_t отражает существенные и типичные черты развития системы, отражаемые анализируемым временным рядом, т.е. последовательными значениями соответствующего экономического показателя. Случайные же отклонения мешают выявить основную тенденцию развития. Наглядным и простым способом выравнивания ряда является фиксация точек на графике и проведение на глаз плавной кривой между ними (и возле них), выражающей исконную тенденцию (рис.В.6).

Такой способ дает приблизительные результаты, иногда все же достаточные для анализа. Однако в сложных случаях применяются математико-статистические методы выравнивания; расчеты при этом ведутся на компьютерах. В частности, с помощью метода наименьших квадратов, сплайн-функции, методов скользящейсредней, экспоненциального сглаживания,аналитического выравнивания и др.

37. Системы эконометрических моделей. Одновременные системы уравнений.

38. Проблема идентификации эконометрических моделей.

Источник

Методы выявления тенденций во временных рядах

Во временных рядах можно наблюдать тенденции трех уровней [1]:

1) среднего уровня;

Тенденция среднего уровня означает сосредоточенность уровней временного ряда вокруг их среднего значения, вычисленного по всей совокупности уровней временного ряда.

Тенденция дисперсии – это изменение отклонений эмпирических значений временного ряда от значений, рассчитанных по уравнению тренда. Ряд как бы «раскачивается» относительно линии, описывающей тренд.

Тенденция автокорреляции – тенденция изменения взаимосвязи между отдельными уровнями временного ряда.

Для определения наличия тренда применяется несколько методов. Рассмотрим некоторые из них.

Метод существенности разности средних уровней. Этот метод основан на проверке разности средних двух равных частей одного и того же ряда. Временной ряд разбивают на две равные по числу членов части, каждая из которых рассматривается как самостоятельная выборочная совокупность, имеющая нормальное распределение. Если временной ряд имеет тенденцию, то средние, вычисленные для каждой половины ряда, должны существенно значимо различаться между собой. Если расхождение незначительно (случайно), то временной ряд не имеет тенденции. Таким образом, проверка наличия тренда в используемом ряду сводится к проверке гипотезы о равенстве средних двух нормально распределенных совокупностей.

Математический аппарат, используемый при проверке существенности разности средних, рассмотрим на примере.

Пример. Пусть даны объемы основных фондов предприятия за 15 лет

Определить наличие тренда методом существенности разности средних.

Решение. 1. Делим ряд на две равные части: .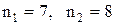

2. Находим средние значения этих совокупностей:

3. Находим дисперсии выборочных совокупностей:

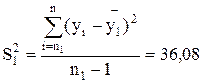
4. Проверим гипотезу об отсутствии тенденции в дисперсии . Используем критерий Фишера:

По таблице критических точек распределения Фишера найдем критическое значение критерия при уровне значимости и для числа степеней свободы большей дисперсии и числа степеней свободы меньшей дисперсии

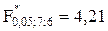
Таким образом, 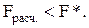Следовательно, нет оснований отвергать нулевую гипотезу об отсутствии тренда – тенденция дисперсии отсутствует.

5. Проверим нулевую гипотезу об отсутствии тенденции в среднем значении: 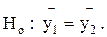Расчетное значение критерия определяется по формуле

Так как 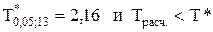, то тенденция в среднем отсутствует.

Метод Фостера-Стьюарта. Фостер и Стьюарт предложили использовать для определения наличия тренда вспомогательные характеристики К и L. Рассмотрим методику выявления тенденций:

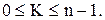
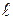
Величина изменяется в пределах от 0 до 1, то есть Если все уровни совпадают, то К=0, если же они монотонно возрастают или убывают, то К=n-1. может принимать значения –1,0,1, тогда L изменяется в пределах от –(n-1) до n-1. L=0, когда тренд отсутствует или когда ряд распадается на равные части с противоположными тенденциями.

Характеристика К служит для выявления тенденции в дисперсии, а L – для обнаружения тенденции в среднем. Для этого проверяется существенно ли величины К и L отклоняются от своих математических ожиданий 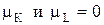. Соответствующие гипотезы проверяются при помощи t-критерия Стьюдента:

Значения 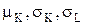табулированы для различных n.

Расчетные значения 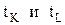сравниваются с табличными с (n-2) степенями свободы. Если , то отклоняется тенденция об отсутствии тенденции в дисперсии, если , то должна быть отклонена как несостоятельная тенденция об отсутствии тренда в среднем.

Пример. Определить наличие тренда в среднем и в дисперсии методом Фостера-Стьюарта для временного ряда

Решение. ,

Для n=9

Так как , то тенденция дисперсии отсутствует, а имеет место тенденция среднего значения.

Сглаживание временных рядов

Проявление случайности и неопределенности в развитии экономических показателей приводит к колебаниям уровней временных рядов, что в какой-то степени искажает истинную тенденцию. Для выявления более четкого тренда используют процедуру сглаживания ряда. Сглаживание – это подравнивание уровней с целью удаления мелких незначительных колебаний показателя.

Методы сглаживания разделяют на две основные группы:

1) аналитическое выравнивание с использованием кривой, проведенной между конкретными уровнями ряда так, чтобы она отображала тенденцию, присущую ряду и одновременно освобождала его от незначительных колебаний;

2) механическое выравнивание отдельных уровней ряда с использованием фактических значений соседних уровней.

Использование первой группы методов предполагает существование некоторой закономерности на протяжении всего динамического ряда. Параметры выбранной кривой остаются неизменными на протяжении всей выравниваемой части ряда. Добавление к выравниваемому ряду новых уровней требует задания новой выравнивающей кривой, что является недостатком этой группы методов.

Суть методов механического сглаживания в следующем. Берется несколько первых членов ряда, образующих так называемый интервал сглаживания. Для них подбирается кривая, аналитическим выражением которой служит полином. С помощью этого полинома определяется новое выровненное значение члена, , находящегося в середине интервала сглаживания. Далее выбранный интервал сдвигается на один уровень вправо, выполняется следующее выравнивание и т.д.

Рассмотрим некоторые из методов механического сглаживания.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Источник