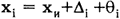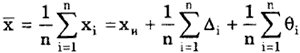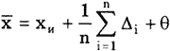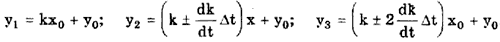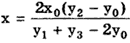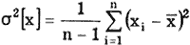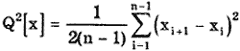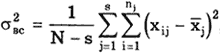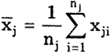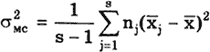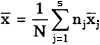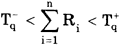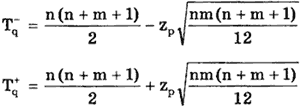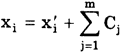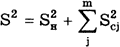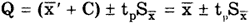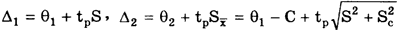Способы выявления систематической погрешности

Способы выявления систематической погрешности

Результаты наблюдений, полученные при наличии систематических погрешностей, будем называть неисправленными и в отличие от исправленных снабжать штрихами их обозначения (например и т.д.). Вычисленные в этих условиях средние арифметические значения и отклонения от результатов наблюдений будем также называть неисправленными и ставить штрихи у символов этих величин. Таким образом,

Поскольку неисправленные результаты наблюдений включают в себя систематические погрешности, сумму которых для каждого -го наблюдения будем обозначать через , то их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на некоторую величину , называемую систематической погрешностью неисправленного среднего арифметического. Действительно,

Если систематические погрешности постоянны, т.е. то неисправленные отклонения могут быть непосредственно использованы для оценки рассеивания ряда наблюдений. В противном случае необходимо предварительно исправить отдельные результаты измерений, введя в них так называемые поправки, равные систематическим погрешностям по величине и обратные им по знаку:

Таким образом, для нахождения исправленного среднего арифметического и оценки его рассеивания относительно истинного значения измеряемой величины необходимо обнаружить систематические погрешности и исключить их путем введения поправок или соответствующей каждому конкретному случаю организации самoгo измерения. Остановимся подробнее на некоторых способах обнаружения систематических погрешностей.

Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от средних арифметических, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основании некоторых априорных знаний об этих погрешностях, получаемых, например, при поверке средств измерений. Измеряемая величина при поверке обычно воспроизводится образцовой мерой, действительное значение которой известно. Поэтому разность между средним арифметическим результатов наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения, равна искомой систематической погрешности.

Ценность полученных при поверке результатов определяется их постоянством в течение некоторого промежутка времени и независимостью от тех изменений внешних условий, которые допустимы при эксплуатации средств измерений с заданной точностью. Тогда полученные при поверке данные могут быть использованы для вычисления поправок, необходимых для исправления результатов наблюдений.

Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических.

Вначале рассмотрим случай, когда в ряде результатов наблюдений предполагается наличие постоянной систематической погрешности. Для того чтобы удостовериться в этом, исследователь, сделав несколько измерений, заменяет некоторые меры или измерительные приборы, включенные в установку и являющиеся предполагаемыми источниками постоянных систематических погрешностей, другими мерами и измерительными приборами и проводит еще несколько измерений.

Рассматриваемый способ обнаружения постоянных систематических погрешностей можно сформулировать следующим образом: если неисправленные отклонения результатов наблюдений резко изменяются при изменении условий наблюдений, то данные результаты содержат постоянную систематическую погрешность, зависящую от условий наблюдений.

При прогрессивной систематической погрешности последовательность неисправленных отклонений результатов наблюдений обнаруживает тенденцию к возрастанию или убыванию. На рис.13 изображена зависимость погрешности измерения от длины измеряемой детали.

Несмотря на большие случайные изменения погрешности тенденция к увеличению ее в отрицательном направлении с ростом измеряемой величины явно обнаруживается. Если бы случайные погрешности были невелики, то значения неисправленных отклонений меняли бы свой знак при некотором среднем значении измеряемой величины. Случайные погрешности несколько искажают эту картину, однако, если они даже одного порядка малости с систематическими погрешностями, в последовательности знаков можно заметить некоторую неравномерность: неисправленные отклонения результатов одного знака чаще встречаются в отрицательной полуплоскости, чем в положительной.

Если же в ряде результатов наблюдений присутствует периодическая систематическая погрешность, то группы знаков плюс и минус в последовательности неисправленных отклонений результатов наблюдений могут периодически сменять друг друга, если, конечно, случайные погрешности не особенно велики.

Обобщая два рассмотренных случая, можно сказать: если последовательность знаков плюс сменяется последовательностью знаков минус или наоборот, то данный ряд результатов наблюдений обнаруживает прогрессивную погрешность, если группы знаков плюс и минус чередуются — периодическую погрешность.

Источник

Методы обнаружения и исключения систематических погрешностей

Для учёта и устранения систематических погрешностей применяют методы, которые условно можно разбить на две группы: теоретические и экспериментальные способы.

1. Теоретические способы возможны, когда может быть получено аналитическое выражение для искомой погрешности на основании априорной информации.

2. Экспериментальные способы также предполагают наличие априорной информации, но лишь качественного характера. Для получения количественной оценки необходимо проведение дополнительных исследований.

Для устранения систематических погрешностей применяются следующие методы:

1. Постоянные систематические погрешности.

а) Метод замещения — осуществляется путем замены измеряемой величины известной величиной так, чтобы в состоянии и действии средства измерений не происходило изменений;

б) Метод противопоставления.

Измерения выполняются с двумя наблюдениями, проводимыми так, чтобы причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений.

в) Метод компенсации погрешности по знаку.

Измерения также проводятся дважды так, чтобы постоянная систематическая погрешность входила в результат измерения с разными знаками. За результат измерения принимается среднее значение двух измерений.

2. Прогрессирующие систематические погрешности.

а) Метод симметричных наблюдений.

Измерения производят с несколькими наблюдениями, проводимыми через равные интервалы времени, затем обрабатывают результаты, вычисляют среднее арифметическое симметрично расположенных наблюдений. Теоретически эти средние значения должны быть равны. Эти данные позволяют контролировать ход эксперимента, а также устранять систематические погрешности.

б) Метод рандомизации.

Этот метод основан на переводе систематических погрешностей в случайные. При этом измерение некоторой физической величины проводят рядом однотипных приборов с дальнейшей статистической обработкой полученных результатов. Уменьшение систематической погрешности достигается и при изменении случайным образом методики и условий проведения измерений. При определёнии значений систематической погрешности, результаты измерений исправляют, то есть вносят либо поправку, или поправочный множитель, но исправленные результаты обязательно содержат не исключенные остатки систематических погрешностей (НСП)

Источник

Способы обнаружения и устранения систематических погрешностей

Результаты наблюдений, полученные при наличии систематической погрешности, называются неисправленными. При проведении измерений стараются в максимальной степени исключить или учесть влияние систематических погрешностей.

Это может быть достигнуто следующими путями:

— устранением источников погрешностей до начала измерений. В большинстве областей измерений известны главные источники систематических погрешностей и разработаны методы, исключающие их возникновение или устраняющие их влияние на результат измерения. В связи с этим в практике измерений стараются устранить систематические погрешности не путем обработки экспериментальных данных, а применением СИ, реализующих соответствующие методы измерений;

— определением поправок и внесением их в результат измерения;

— оценкой границ неисключенных систематических погрешностей.

Постоянная систематическая погрешность не может быть найдена методами совместной обработки результатов измерений. Однако она не искажает ни показатели точности измерений, характеризующие случайную погрешность, ни результат нахождения переменной составляющей систематической погрешности. Действительно, результат одного измерения

где x_и — истинное значение измеряемой величины; _i — i-я случайная погрешность; _i — i-я систематическая погрешность. После устранения результатов многократных измерении получаем среднее арифметическое значение измеряемой величины

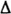
Если систематическая погрешность постоянна во всех измерениях, т.е. _i= ,то

Таким образом, постоянная систематическая погрешность не устраняется при многократных измерениях.

Постоянные систематические погрешности могут быть обнаружены лишь путем сравнения результатов измерений с другими, полученными с помощью более высокоточных методов и средств. Иногда эти погрешности могут быть устранены специальными приемами проведения процесса измерений. Эти методы рассмотрены ниже.

Наличие существенной переменной систематической погрешности искажает оценки характеристик случайной погрешности и аппроксимацию ее распределения. Поэтому она должна обязательно выявляться и исключаться из результатов измерений.

Для устранения постоянных систематических погрешностей применяют следующие методы:

— Метод замещения, представляющий собой разновидность метода сравнения, когда сравнение осуществляется заменой измеряемой величины известной величиной, причем так, что при этом в состоянии и действии всех используемых средств измерений не происходит никаких изменений. Этот метод дает наиболее полное решение задачи. Для его реализации необходимо иметь регулируемую меру, величина которой однородна измеряемой. Например, взвешивание по методу Борда, измерение сопротивления посредством моста постоянного тока и мер сопротивления.

— Метод противопоставления, являющийся разновидностью метода сравнения, при котором измерение выполняется дважды и проводится так, чтобы в обоих случаях причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений. Например, способ взвешивания Гаусса.

— Метод компенсации погрешности по знаку (метод изменения знака систематической погрешности), предусматривающий измерение с двумя наблюдениями, выполняемыми так, чтобы постоянная систематическая погрешность входила в результат каждого из них с разными знаками.

— Метод рандомизации — наиболее универсальный способ исключения неизвестных постоянных систематических погрешностей. Суть его состоит в том, что одна и та же величина измеряется различными методами (приборами). Систематические погрешности каждого из них для всей совокупности являются разными случайными величинами. -Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности взаимно компенсируются.

Для устранения переменных и монотонно изменяющихся систематических погрешностей применяют следующие приемы и методы.

— Анализ знаков неисправленных случайных погрешностей.

Если знаки неисправленных случайных погрешностей чередуются с какой-либо закономерностью, то наблюдается переменная систематическая погрешность. Если последовательность знаков «+» у случайных погрешностей сменяется последовательностью знаков «-» или наоборот, то присутствует монотонно изменяющаяся систематическая погрешность. Если группы знаков «+» и «-» у случайных погрешностей чередуются, то присутствует периодическая систематическая погрешность.

— Графический метод.

Он является одним из наиболее простых способов обнаружения переменной систематической погрешности в ряду результатов наблюдений и заключается в построении графика последовательности неисправленных значений результатов наблюдений. На графике через построенные точки проводят плавную кривую, которая выражает тенденцию результата измерения, если она существует. Если тенденция не прослеживается, то переменную систематическую погрешность считают практически отсутствующей.

— Метод симметричных наблюдений.

Рассмотрим сущность этого метода на примере измерительного преобразователя, передаточная функция которого имеет вид y = kx + y₀ , где х, у — входная и выходная величины преобразователя; k — коэффициент, погрешность которого изменяется во времени по линейному закону; у₀ — постоянная.
Для устранения систематической погрешности трижды измеряется выходная величина у через равные промежутки времени At. При первом и третьем измерениях на вход преобразователя подается сигнал х0 от образцовой меры. В результате измерений получается система уравнений:

Ее решение позволяет получить значение х, свободное от переменной систематической погрешности, обусловленной изменением коэффициента k:

Специальные статистические методы. К ним относятся способ последовательных разностей, дисперсионный анализ, и др. Рассмотрим подробнее некоторые из них.

Способ последовательных разностей (критерий Аббе).

Применяется для обнаружения изменяющейся во времени систематической погрешности и состоит в следующем. Дисперсию результатов наблюдений можно оценить двумя способами: обычным

и вычислением суммы квадратов последовательных (в порядке проведения измерений) разностей ( x_i+1 — x_i) 2

Если в процессе измерений происходило смещение центра группирования результатов наблюдений, т.е. имела место переменная систематическая погрешность, то 2 [x] дает преувеличенную оценку дисперсии результатов наблюдений. Это объясняется тем, что на 2 [x] влияют вариации . В то же время изменения центра группирования весьма мало сказываются на значениях последовательных разностей d _i = x _i+1-x _i, поэтому смещения почти не отразятся на значении Q 2 [x].

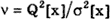
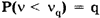
Отношение является критерием для обнаружения систематических смещений центра группирования результатов наблюдений. Критическая область для этого критерия (критерия Аббе) определяется как , где q = 1-Р — уровень значимости, Р — доверительная вероятность. Значения v_q для различных уровней значимости q и числа наблюдений n приведены в таблице. Если полученное значение критерия Аббе меньше при заданных q и n, то гипотеза о постоянстве центра группирования результатов наблюдений отвергается, т.е. обнаруживается переменная систематическая погрешность результатов измерений.

n	vq при q, равном	n	vq при q, равном
0.001	0.01	0.05	0.001	0.01	0.05
0.295	0.313	0.390	0.295	0.431	0.578
0.208	0.269	0.410	0.311	0.447	0.591
0.182	0.281	0.445	0.327	0.461	0.603
0.185	0.307	0.468	0.341	0.474	0.614
0.202	0.331	0.491	0.355	0.487	0.624
0.221	0.354	0.512	0.368	0.499	0.633
0.241	0.376	0.531	0.381	0.510	0.642
0.260	0.396	0.548	0.393	0.520	0.650
0.278	0.414	0.564

Дисперсионный анализ (критерий Фишера).

В практике измерений часто бывает необходимо выяснить наличие систематической погрешности результатов наблюдений, обусловленной влиянием какого-либо постоянно действующего фактора, или определить, вызывают ли изменения этого фактора систематическое смещение результатов измерений. В данном случае проводят многократные измерения, состоящие из достаточного числа серий, каждая из которых соответствует определенным (пусть неизвестным, но различным) значениям влияющего фактора. Влияющими факторами, по которым производится объединение результатов наблюдений по сериям, могут быть внешние условия (температура, давление и т.д.), временная последовательность проведения измерений и т.п.

После проведения N измерений их разбивают на s серий (s > 3) по n_j результатов наблюдений ( sn_j = N ) в каждой серии и затем устанавливают, имеется или отсутствует систематическое расхождение между результатами наблюдений в различных сериях. При этом должно быть установлено, что результаты в сериях распределены нормально. Рассеяние результатов наблюдений в пределах каждой серии отражает только случайные влияния, характеризует лишь случайные погрешности измерений в пределах этой серии. Характеристикой совокупности случайных внутрисерийных погрешностей будет средняя сумма дисперсий результатов наблюдений, вычисленных раздельно для каждой серии, т.е.

где x_ji — результат i-го измерения в j-й серии.
Внутрисерийная дисперсия 2 _BC характеризует случайные погрешности измерений, так как только случайные влияния обусловливают те различия (отклонения результатов наблюдений), на которых она основана. В то же время рассеяние _j различных серий обусловливается не только случайными погрешностями измерений, но и систематическими различиями (если они существуют) между результатами наблюдений, сгруппированными по сериям. Следовательно, усредненная межсерийная дисперсия

где , выражает силу действия фактора, вызывающего систематические различия между сериями.

Таким образом, 2 _BC /( 2 _BC + 2 _MC) характеризует долю дисперсии всех результатов наблюдений, обусловленную наличием случайных погрешностей измерений, а 2 _MC /( 2 _BC + 2 _MC) — долю дисперсии, обусловленную межсерийными различиями результатов наблюдений. Первую из них называют коэффициентом ошибки, вторую — показателем дифференциации. Чем больше отношение показателя дифференциации к коэффициенту ошибки, тем сильнее действие фактора, по которому группировались серии, и тем больше систематическое различие между ними.

Критерием оценки наличия систематических погрешностей в данном случае является дисперсионный критерий Фишера F = 2 _MC 2 _BC. Критическая область для критерия Фишера соответствует P (F>F_q) = q.

Значения F_q для различных уровней значимости q, числа измерений N и числа серий s приведены в приложении 1, где k₂ = N-s , k₁ = s-1. Если полученное значение критерия Фишера больше F_q (при заданных q, N и s), то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность, вызываемая тем фактором, по которому группировались результаты наблюдений.

Из всех рассмотренных способов обнаружения систематических погрешностей дисперсионный анализ является наиболее эффективным и достоверным, так как позволяет не только установить факт наличия погрешности, но и дает возможность проанализировать источники ее возникновения.

Если закон распределения результатов измерений неизвестен, то для обнаружения систематической погрешности применяют статистический критерий Вилкоксона.

Из двух групп результатов измерений x₁, x₂. x_n и y₁, y₂. y_m , n> = m> = 5 , составляется вариационный ряд, в котором все n + m значений x₁, x₂. x_n и y₁, y₂. y_m располагают в порядке их возрастания и приписывают им ранги — порядковые номера членов вариационного ряда. Различие средних значений каждого из рядов можно считать допустимым, если выполняется неравенство

где R_i — ранг (номер) члена x_i, равный его номеру в вариационном ряду T — _q и T + _q — нижнее и верхнее критические значения для выбранного уровня значимости q.

При mm>15 они рассчитываются по формулам:

где z_p — квантиль нормированной функции Лапласа.

Таблица. Критические значения T_q — и T_q + при q=0.05 и 0,01

n	m	q=0.05	q=0.01
Tq —	Tq +	Tq —	Tq +

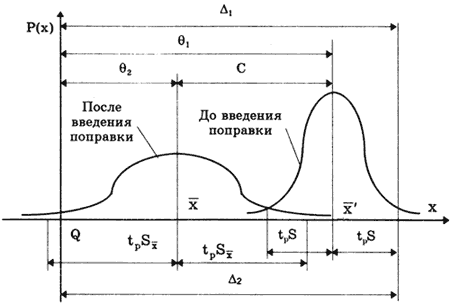
Исключение систематических погрешностей путем введения поправок.

В ряде случаев систематические погрешности могут быть вычислены и исключены из результата измерения. Для этого используются поправки. Поправка C_j — величина, одноименная измеряемой, которая вводится в результат измерения x_i = x_i ‘ + _j + C_j с целью исключения составляющих систематической погрешности _j. При C_j = —_j j-я составляющая систематической погрешности полностью устраняется из результата измерения. Поправки определяются экспериментально или в результате специальных теоретических исследований. Они задаются в виде таблиц, графиков или формул.

Введением одной поправки устраняется влияние только одной составляющей систематической погрешности. Для устранения всех составляющих в результат измерения приходится вводить множество поправок. При этом вследствие ограниченной точности определения поправок случайные погрешности результата измерения накапливаются и его дисперсия увеличивается. Так как поправка известна с определенной точностью, то она характеризуется статистически — средним значением поправки С и СКО S_c. При исправлении результата x_i ‘ путем введения поправок C_j , где j = l, 2. m, по формуле

дисперсия исправленного результата

где S_н 2 — оценка дисперсии неисправленного результата; S_cj 2 — оценка дисперсии j-й поправки. Как видно, с одной стороны, уточняется результат измерения, а с другой — увеличивается разброс за счет роста дисперсии. Следовательно, необходимо найти оптимум.
Пусть при измерении постоянной величины Q получено значение Q = ‘ t _pS ,где — оценка среднего арифметического неисправленного результата измерений; t_p — коэффициент Стьюдента.

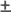
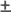
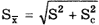
После введения поправки C t_pS_c результат измерения

где .
Максимальные доверительные значения погрешности результата измерения до и после введения поправки равны соответственно

Поправку имеет смысл вводить до тех пор, пока 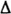₁ 0.5S_c 2 /S 2 . Из этого неравенства видно, что если оценка среднего квадратического отклонения поправки S_c стремится к нулю, то поправку имеет смысл вводить всегда. В практических расчетах погрешность результата обычно выражается не более чем двумя значащими цифрами, поэтому поправка, если она меньше пяти единиц младшего разряда, следующего за последним десятичным разрядом погрешности результата, все равно будет потеряна при округлении и вводить ее не имеет смысла.

Источник