Методы выявления основной тенденции (тренда) в рядах динамики
Поможем написать любую работу на аналогичную тему
Одна из основных задач изучения рядов динамики – выявить основную тенденцию (закономерность) в изменении уровней ряда, именуемую трендом. Закономерность в изменении уровней ряда в одних случаях проявляется наглядно, в других – может маскироваться колебаниями случайного или неслучайного характера. Поэтому, чтобы сделать правильные выводы о закономерностях развития того или иного показателя, надо суметь отделить тренд от колебаний, вызванных случайными кратковременными причинами. На основании выделенного тренда можно экстраполировать (прогнозировать) развитие явления в будущем. С этой целью (устранить колебания, вызванные случайными причинами) ряды динамики подвергают обработке.
Существует несколько методов обработки рядов динамики, помогающих выявить основную тенденцию изменения уровней ряда, а именно: метод укрупнения интервалов, метод скользящей средней и аналитическое выравнивание. Во всех методах вместо фактических уровней при обработке ряда рассчитываются иные (расчетные) уровни, в которых тем или иным способом взаимопогашается действие случайных факторов и тем самым уменьшается колеблемость уровней. Последние в результате становятся как бы «выравненными», «сглаженными» по отношению к исходным фактическим данным. Такие методы обработки рядов динамики называются сглаживанием или выравниванием рядов динамики.
Простейший метод сглаживания уровней ряда – укрупнения интервалов, для определяется итоговое значение или средняя величина исследуемого показателя. Этот метод особенно эффективен, если первоначальные уровни ряда относятся к коротким промежуткам времени. Например, если имеются данные о ежесуточном производстве мороженого на предприятии за месяц, то, естественно, в таком ряду возможны значительные колебания уровней, так как чем меньше период, за который приводятся данные, тем больше влияние случайных факторов. Чтобы устранить это влияние, рекомендуется укрупнить интервалы времени, например до 5 или 10 дней, и для этих укрупненных интервалов рассчитать общий или среднесуточный объем производства (соответственно по пятидневкам или декадам). В ряду с укрупненными интервалами времени закономерность изменения уровней будет более наглядной. Или, например, имеются ежемесячные данные о производстве мороженого – табл.32, еще более сильно укрупним интервалы – до трех месяцев (см. табл.33).
По своей сути метод скользящей средней похож на метод укрупнения интервалов, но в данном случае фактические уровни заменяются средними уровнями, рассчитанными для последовательно подвижных (скользящих) укрупненных интервалов, охватывающих m уровней ряда. Например, если принять m=3, то сначала рассчитывается средняя величина из первых трех уровней, затем находится средняя величина из 2-го, 3-го и 4-го уровней, потом из 3-го, 4-го и 5-го и т.д., т.е. каждый раз в сумме трех уровней появляется новый уровень, а два остаются прежними, что и обусловливает взаимопогашение случайных колебаний в средних уровнях. Рассчитанные из m членов скользящие средние относятся к середине (центру) каждого рассматриваемого интервала.
Сглаживание методом скользящей средней можно проводить по любому числу членов m, но удобнее, если m – нечетное число, так как в этом случае скользящая средняя сразу относится к конкретной временнОй точке – середине (центру) интервала. Если же m – четное, то скользящая средняя относится к промежутку между временнЫми точками: например, при сглаживании по четырем членам (m=4) средняя из первых четырех уровней будет находиться между второй и третьей временной точкой, следующая – между третьей и четвертой и т.д. Тогда, чтобы сглаженные уровни относились непосредственно к конкретным временнЫм точкам, из каждой пары смежных промежуточных значений скользящих средних находят среднюю арифметическую, которую относят к временной точке, находящейся между смежными. Такой прием двойного расчета сглаженных уровней называется центрированием.
Недостатком метода скользящей средней является то, что сглаженный ряд укорачивается по сравнению с фактическим с двух концов: при нечетном m на (m-1)/2, а при четном m – на m/2 с каждого конца. Применяя этот метод, надо помнить, что он сглаживает (устраняет) лишь случайные колебания. Если же, например, ряд содержит сезонную волну (см. 6.6), она сохранится и после сглаживания методом скользящей средней. Кроме того, этот метод сглаживания, как и метод укрупнения интервалов не позволяет выражать общую тенденцию изменения уровней в виде математической модели.
Наиболее совершенным методом обработки рядов динамики в целях устранения случайных колебаний и выявления тренда является выравнивание уровней ряда по аналитическим формулам (или аналитическое выравнивание). Суть аналитического выравнивания заключается в замене эмпирических (фактических, исходных) уровней yi теоретическими 
, которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени: 
= f(t).
При этом каждый фактический уровень yi рассматривается обычно как сумма двух составляющих:
, (90)
где f(t) = - систематическая составляющая, отражающая тренд и выраженная определенным уравнением; 
— случайная величина, вызывающая колебания уровней вокруг тренда.
Задача аналитического выравнивания сводится к следующему:
1) определение на основе фактических данных формы (вида) гипотетической функции = f(t), способной наиболее адекватно отразить тенденцию развития исследуемого показателя;
2) нахождение по эмпирическим данным параметров указанной функции (уравнения);
3) расчет по найденному уравнению теоретических (выравненных) уровней.
В аналитическом выравнивании наиболее часто используются простейшие функции, представленные в табл. 30, где обозначено — теоретические (выравненные) уровни (читается как «игрек, выравненный по t»); t – условное обозначение времени (1, 2, 3 …); a0, a1, a2, . – параметры аналитической функции; k – число гармоник (при выравнивании по ряду Фурье).
Выбор той или иной функции для выравнивания ряда динамики осуществляется на основании графического изображения эмпирических данных. Если по тем или иным причинам уровни эмпирического ряда трудно описать одной функцией, следует разбить анализируемый период на отдельные части и затем выровнять каждую часть по соответствующей кривой.
Таблица 30. Виды математических функций[30], используемые при выравнивании
Источник
Методы анализа тенденций рядов динамики
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер.
Основная тенденция (тренд) – изменение, определяющее общее направление развития, это систематическая составляющая долговременного действия.
Задача – выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов.
Методы выявления тренда:
1) Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Средняя, исчисленная по укрупненным интервалам, позволяет выявить направление и характер (ускорение или замедление роста) основной тенденции развития, в то время как слишком малые интервалы между наблюдениями приводят к появлению ненужных деталей в динамике процесса, засоряющих общую тенденцию.
| Месяц | Объем выпуска, млн.руб. | Месяц | Объем выпуска, млн.руб. |
| Январь | 5,1 | Июль | 5,6 |
| Февраль | 5,4 | Август | 5,9 |
| Март | 5,2 | Сентябрь | 6,1 |
| Апрель | 5,3 | Октябрь | 6,0 |
| Май | 5,6 | Ноябрь | 5,9 |
| Июнь | 5,8 | Декабрь | 6,2 |
Различные направления изменений уровней ряда по отдельным месяцам затрудняют выводы об основной тенденции производства. Если соответствующие месячные уровни объединить в квартальные и вычислить среднемесячный выпуск продукции по кварталам, т.е. укрупнить интервалы, то решение задачи упрощается.
| Квартал | Объем производства, млн.руб. |
| в квартал | в среднем в месяц |
| 15,7 | 5,23 |
| 16,7 | 5,57 |
| 17,6 | 5,87 |
| 18,1 | 6,03 |
После укрупнения интервалов основная тенденция роста производства стала очевидной: 5,23
Укрупнение интервалов и метод скользящей средней дают возможность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных или волнообразных колебаний. Получить обобщенную статистическую модель тренда посредством этих методов нельзя.
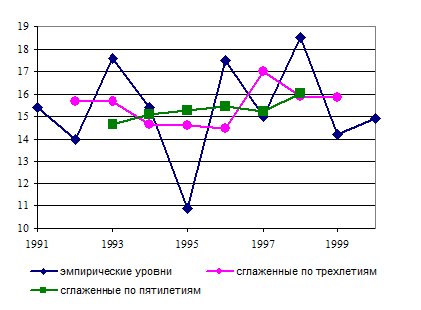
Рис. 8.2. Эмпирические и сглаженные уровни ряда динамики
3) Аналитическое выравнивание ряда динамики используется для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней ряда динамики во времени.
Общая тенденция развития рассчитывается как функция времени:
где t – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.
Определение теоретических (расчетных) уровней t производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики.
Простейшими моделями, выражающими тенденцию развития, являются (где a0, a1 – параметры уравнения; t – время):
Показательная функция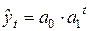
. (6.18)
Расчет параметров функции обычно производится методом наименьших квадратов. Выравнивание ряда динамики заключается в замене фактических уровней yi плавно изменяющимися уровнями t, наилучшим образом аппроксимирующими статистические данные.
Выравнивание по прямой используется в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии.
Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны.
Выравнивание ряда динамики по прямой t = a0 + a1 · t. Параметры a0, a1 согласно МНК находятся решением следующей системы нормальных уравнений:
(6.20)
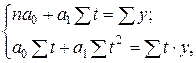
где y – фактические (эмпирические) уровни ряда;
t – время (порядковый номер периода или момента времени).
S t = 0, так что система нормальных уравнений (8.20) принимает вид:
(6.21)
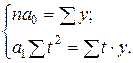
Отсюда можно выразить коэффициенты регрессии:
; (6.22)
. (8.23)
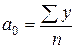
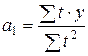
Если расчеты выполнены правильно, то S y = S ?t.
Источник
Способы выявления основной тенденции ряда динамики
7.5 чЩСЧМЕОЙЕ ПУОПЧОПК ФЕОДЕОГЙЙ ТСДБ ДЙОБНЙЛЙ
пДОБ ЙЪ ЧБЦОЕКЫЙИ ЪБДБЮ БОБМЙЪБ ТСДБ ДЙОБНЙЛЙ ЪБЛМАЮБЕФУС Ч ХУФБОПЧМЕОЙЙ ЪБЛПОПНЕТОПУФЕК ТБЪЧЙФЙС СЧМЕОЙС ЙМЙ РТПГЕУУБ. ч ЬФЙИ ГЕМСИ ПРТЕДЕМСЕФУС ПУОПЧОБС ФЕОДЕОГЙС ТБЪЧЙФЙС (ФТЕОД).
дМС ЧЩСЧМЕОЙС ПУОПЧОПК ФЕОДЕОГЙЙ РТЙНЕОСАФУС ТБЪМЙЮОЩЕ РТЙЕНЩ Й НЕФПДЩ. пДОЙН ЙЪ РТЙЕНПЧ СЧМСЕФУС НЕФПД ХЛТХРОЕОЙС ЙОФЕТЧБМПЧ. пО ЪБЛМАЮБЕФУС Ч РТЕПВТБЪПЧБОЙЙ РЕТЧПОБЮБМШОПЗП ТСДБ ДЙОБНЙЛЙ Ч ТСДЩ ВПМЕЕ РТПДПМЦЙФЕМШОЩИ РЕТЙПДПЧ (НЕУСЮОЩЕ Ч ЛЧБТФБМШОЩЕ, ЛЧБТФБМШОЩЕ Ч ЗПДПЧЩЕ Й Ф.Д.) оБРТЙНЕТ, ТСД ЕЦЕУХФПЮОПЗП ЧЩРХУЛБ РТПДХЛГЙЙ ЪБНЕОСЕФУС ТСДПН НЕУСЮОПЗП ЧЩРХУЛБ РТПДХЛГЙЙ Й Ф.Д.
дТХЗПК РТЙЕН — НЕФПД УЛПМШЪСЭЕК УТЕДОЕК. еЗП УХФШ УПУФПЙФ Ч ФПН, ЮФП ЧЩЮЙУМСЕФУС УТЕДОЙК ХТПЧЕОШ ЙЪ ПРТЕДЕМЕООПЗП ЮЙУМБ РЕТЧЩИ РП РПТСДЛХ ХТПЧОЕК ТСДБ, ЪБФЕН — УТЕДОЙК ХТПЧЕОШ ЙЪ ФБЛПЗП ЦЕ ЮЙУМБ ХТПЧОЕК, ОБЮЙОБС УП ЧФПТПЗП, ДБМЕЕ — ОБЮЙОБС У ФТЕФШЕЗП Й Ф.Д.
рТЙ ТБУЮЕФБИ УТЕДОЕЗП ХТПЧОС ЛБЛ ВЩ «УЛПМШЪСФ» РП ТСДХ ДЙОБНЙЛЙ ПФ ЕЗП ОБЮБМБ Л ЛПОГХ, ЛБЦДЩК ТБЪ ПФВТБУЩЧБС, ПДЙО ХТПЧЕОШ Ч ОБЮБМЕ Й ДПВБЧМСС ПДЙО УМЕДХАЭЙК.
бМЗПТЙФН ТБУЮЕФБ УЛПМШЪСЭЕК УТЕДОЕК ВПМЕЕ РПДТПВОП ЙЪМПЦЕО [12, У.366-367]
оБ РТЙНЕТЕ ДБООЩИ ФБВМ. 7.9 РТПЙЪЧЕДЕН УЗМБЦЙЧБОЙЕ ТСДБ НЕФПДПН ФТЕИЮМЕООПК УЛПМШЪСЭЕК УТЕДОЕК.
уЗМБЦЙЧБОЙЕ ТЕБМЙЪБГЙЙ ЖЙТНПК РТПДХЛФБ н ЪБ 1991 — 1999 ЗЗ.
НЕФПДПН УЛПМШЪСЭЕК УТЕДОЕК
| зПД | фЩУ. ЫФ. | фТЕИЮМЕООЩЕ УЛПМШЪСЭЙЕ УХННЩ | фТЕИЮМЕООЩЕ УЛПМШЪСЭЙЕ УТЕДОЙЕ |
| б | 1 | 2 | 3 |
| 1991 | 375 | — | — |
| 1992 | 263 | — | 311,7 |
| 1993 | 297 | 935 | 269,0 |
| 1994 | 247 | 807 | 290,0 |
| 1995 | 326 | 870 | 313,0 |
| 1996 | 366 | 939 | 344,3 |
| 1997 | 341 | 1033 | 337,3 |
| 1998 | 305 | 1012 | 315,0 |
| 1999 | 299 | 945 | — |
чЪСЧ ДБООЩЕ ЪБ РЕТЧЩЕ ФТЙ ЗПДБ, ЙУЮЙУМСЕН ФТЕИЮМЕООЩЕ УХННЩ (ЗТ.2 ФБВМ. 7.9), Б ЪБФЕН УТЕДОЙЕ (ЗТ.3 ФБВМ.7.9);
Й Ф.Д.
оБОЕУЕН ОБ ЗТБЖЙЛ ЙУИПДОЩЕ Й ЧЩТБЧОЕООЩЕ ХТПЧОЙ.
тЙУ. 7.1 дЙОБНЙЛБ ТЕБМЙЪБГЙЙ РТПДХЛФБ н ЖЙТНПК «тХВЙО» ЪБ 1991 — 1999 ЗЗ.
лБЛ ЧЙДОП ЙЪ ТЙУХОЛБ 7.1, УЛПМШЪСЭБС УТЕДОСС ДБЕФ ВПМЕЕ РМБЧОПЕ ЙЪНЕОЕОЙЕ ХТПЧОЕК ТСДБ.
оБЙВПМЕЕ ЬЖЖЕЛФЙЧОЩН УРПУПВПН ЧЩСЧМЕОЙС ПУОПЧОПК ФЕОДЕОГЙЙ ТБЪЧЙФЙС СЧМСЕФУС БОБМЙФЙЮЕУЛПЕ ЧЩТБЧОЙЧБОЙЕ. рТЙ ЬФПН ПУОПЧОБС ФЕОДЕОГЙС ТБЪЧЙФЙС Хt ТБУУЮЙФЩЧБЕФУС ЛБЛ ЖХОЛГЙС ЧТЕНЕОЙ
пРТЕДЕМЕОЙЕ ФЕПТЕФЙЮЕУЛЙИ (ТБУЮЕФОЩИ) ХТПЧОЕК Х t i РТПЙЪЧПДЙФУС ОБ ПУОПЧЕ БДЕЛЧБФОПК НБФЕНБФЙЮЕУЛПК ЖХОЛГЙЙ, ЛПФПТБС ОБЙМХЮЫЙН ПВТБЪПН ПФПВТБЦБЕФ ПУОПЧОХА ФЕОДЕОГЙА ТСДБ ДЙОБНЙЛЙ.
рПДВПТ БДЕЛЧБФОПК ЖХОЛГЙЙ ПУХЭЕУФЧМСЕФУС НЕФПДПН ОБЙНЕОШЫЙИ ЛЧБДТБФПЧ — НЙОЙНБМШОПУФША ПФЛМПОЕОЙК УХННЩ ЛЧБДТБФПЧ НЕЦДХ ФЕПТЕФЙЮЕУЛЙНЙ Х t i ХТПЧОСНЙ:
 . | (7.11) |
тБУУНПФТЙН РТЙНЕОЕОЙЕ НЕФПДБ БОБМЙФЙЮЕУЛПЗП ЧЩТБЧОЙЧБОЙС РП РТСНПК ДМС ЧЩТБЦЕОЙС ПУОПЧОПК ФЕОДЕОГЙЙ ОБ УМЕДХАЭЕН РТЙНЕТЕ.
ч ФБВМЙГЕ 7.10 РТЙЧЕДЕОЩ ЙУИПДОЩЕ Й ТБУЮЕФОЩЕ ДБООЩЕ П ТПЪОЙЮОПН ФПЧБТППВПТПФЕ ТЕЗЙПОБ ЪБ 1994-1998 ЗЗ.
| зПДЩ | нМТД. ТХВ. | t | t 2 | ty | yt |
| 1994 | 16,4 | -2 | 4 | -32,8 | 16,34 |
| 1995 | 16,9 | -1 | 1 | -16,9 | 17,02 |
| 1996 | 17,8 | 0 | 0 | 0 | 17,70 |
| 1997 | 18,3 | 1 | 1 | 18,3 | 18,38 |
| 1998 | 19,1 | 2 | 4 | 38,2 | 19,06 |
| йФПЗП | 88.5 | — | 10 | 6,8 | 88,50 |
дМС ЧЩТБЧОЙЧБОЙС ТСДБ ДЙОБНЙЛЙ РП РТСНПК ЙУРПМШЪХЕН ХТБЧОЕОЙЕ Хt = aП + Б 1 t дМС ХРТПЭЕОЙС ТБУЮЕФПЧ РБТБНЕФТЩ ХТБЧОЕОЙС НПЗХФ ВЩФШ ПРТЕДЕМЕОЩ У РПНПЭША УРПУПВБ ПФУЮЕФБ ПФ ХУМПЧОПЗП ОХМС, УХФШ ЛПФПТПЗП ЪБЛМАЮБЕФУС Ч ФПН, ЮФП РПЛБЪБФЕМСН ЧТЕНЕОЙ t РТЙДБАФ ФБЛЙЕ ЪОБЮЕОЙС, ЮФПВЩ ЙИ УХННБ ВЩМБ ТБЧОБ ОХМА, Ф.Е. S t=0. [12, 378-379]
рБТБНЕФТЩ ХТБЧОЕОЙС ТБУУЮЙФЩЧБАФУС РП ЖПТНХМБН:
| a 0 = S y/n; | (7.12) |
| a 1 = S ty/ S t 2 . | (7.13) |
тБУЮЕФ ОЕПВИПДЙНЩИ ЪОБЮЕОЙК ДБО Ч ФБВМЙГЕ 7.10.
рП ЙФПЗПЧЩН ДБООЩН РПМХЮБЕН РБТБНЕФТЩ ХТБЧОЕОЙС:
ч ТЕЪХМШФБФЕ РПМХЮБЕН УМЕДХАЭЕЕ ХТБЧОЕОЙЕ ПУОПЧОПК ФЕОДЕОГЙЙ ТПЪОЙЮОПЗП ФПЧБТППВПТПФБ ТЕЗЙПОБ ЪБ 1994-1998ЗЗ:
рПДУФБЧМСС Ч ХТБЧОЕОЙЕ РТЙОСФЩЕ ПВПЪОБЮЕОЙС t, ЧЩЮЙУМЙН ЧЩТБЧОЕООЩЕ ХТПЧОЙ ТСДБ ДЙОБНЙЛЙ:
1994З — Х 1 = 17,7 + 0,68 ћ (-2) = 16,34
Й Ф.Д. (УН. ЪОБЮЕОЙС Хt Ч ФБВМ. 7.10)
оБОЕУЕН ОБ ЗТБЖЙЛ ЙУИПДОЩЕ Й ФЕПТЕФЙЮЕУЛЙЕ ЪОБЮЕОЙС ХТПЧОЕК ТСДБ ДЙОБНЙЛЙ.
тЙУ. 7.2 дЙОБНЙЛБ ТПЪОЙЮОПЗП ФПЧБТППВПТПФБ ТЕЗЙПОБ Ч 1994-1998ЗЗ.
Источник
