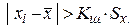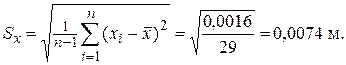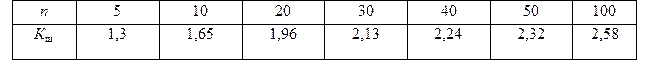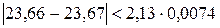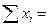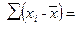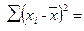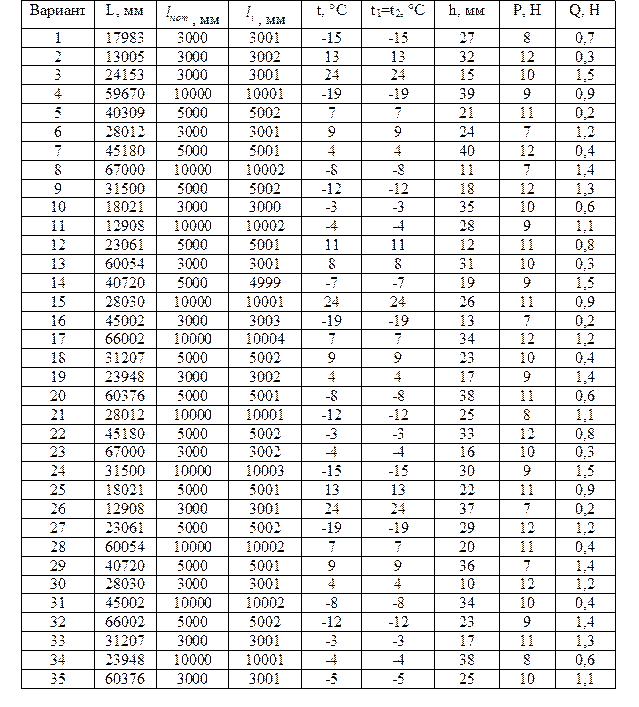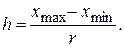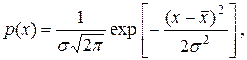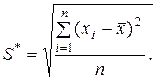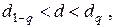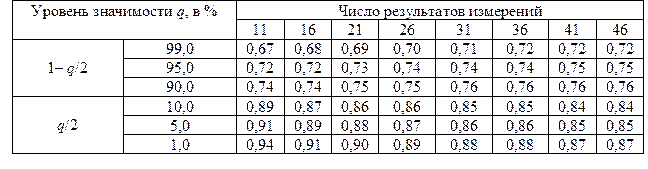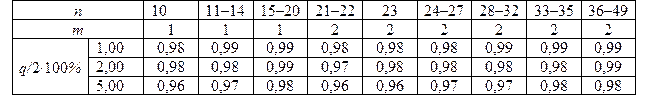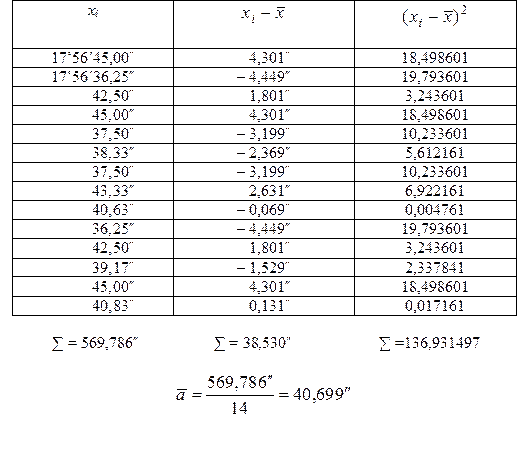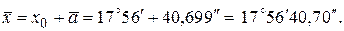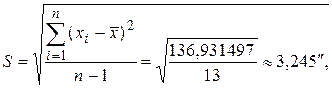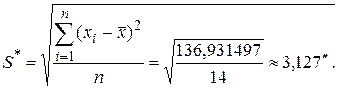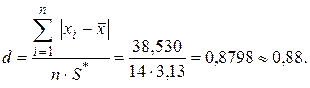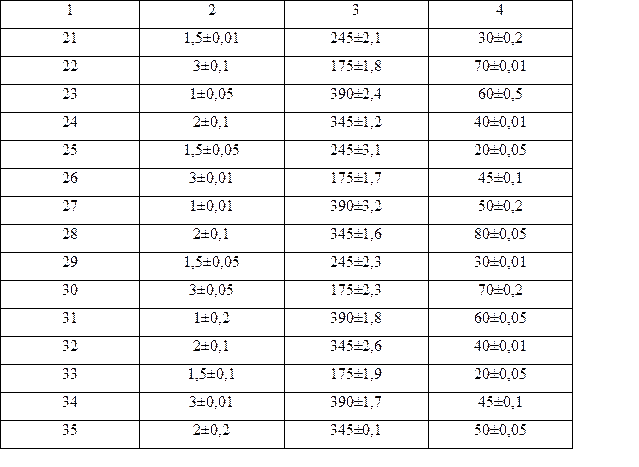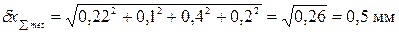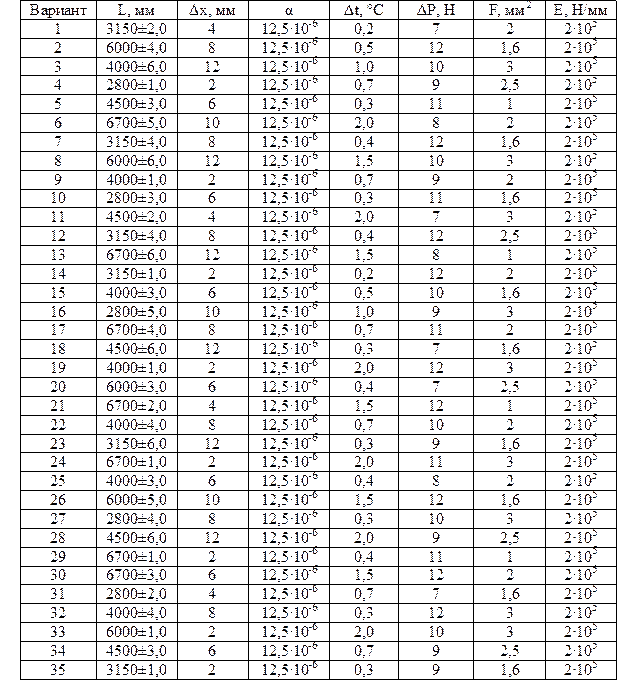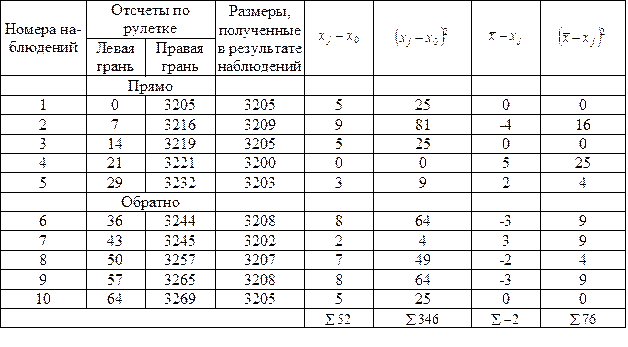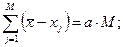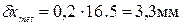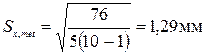Способы выявления грубых погрешностей
В начале главы уже было отмечено, что грубыми называют погрешности, явно превышающие по своему значению погрешности, оправданные условиями проведения эксперимента. Для их устранения желательно еще перед измерениями определить значение искомой величины приближенно, с тем чтобы в дальнейшем можно было сконцентрировать внимание лишь на уточнении предварительных данных. Если оператор в процессе измерений обнаруживает, что результат одного из наблюдений резко отличается от других, и находит причины этого, то он, конечно, вправе отбросить этот результат и провести повторные измерения. Но необдуманное отбрасывание резко отличающихся от других результатов может привести к существенному искажению характеристик рассеивания ряда измерений, поэтому повторные измерения лучше проводить не взамен сомнительных, а в дополнение к ним.
Особенно остро ставится вопрос об устранении грубых погрешностей при обработке уже имеющегося материала, когда невозможно учесть все обстоятельства, при которых проводили измерения. В этом случае приходится прибегать к чисто статистическим методам.
Вопрос о том, содержит ли данный результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез.
Проверяемая гипотеза состоит в утверждении, что результат наблюдения не содержит грубой погрешности, т.е. является одним из значений случайной величины Х с законом распределения , статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший или наименьший из результатов наблюдений. Поэтому для проверки гипотезы следует воспользоваться распределениями величин
Функции их распределения определяют методами теории вероятностей [3]. Они совпадают между собой и для нормального распределения результатов наблюдений протабулированы и представлены в табл.П.7 приложения. По данным этой таблицы, при заданной доверительной вероятности или уровне значимости можно для количества измерения найти те наибольшие значения , которые случайная величина может еще принять по чисто случайным причинам.
Если вычисленное по опытным данным значение окажется меньше , то гипотеза принимается; в противном случае ее следует отвергнуть как противоречащую данным наблюдений. Тогда результат или соответственно приходится рассматривать как содержащий грубую погрешность и не принимать его во внимание при дальнейшей обработке результатов наблюдений.
Источник
Способы обнаружения и исключения грубых погрешностей



Грубая погрешность или промах – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором. К ним можно отнести:
— неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
— неправильная запись результата наблюдений, значений отдельных мер использованного набора, например гирь;
— хаотические изменения параметров питающего СИ напряжения, например его амплитуды или частоты.
Грубые погрешности, как правило, возникают при однократных измерениях и обычно устраняются путем повторных измерений. Их причинами могут быть внезапные и кратковременные изменения условий измерения или оставшиеся незамеченными неисправности в аппаратуре. При многократных измерениях для обнаружения промахов используют статистические критерии.
Для выявления грубых погрешностей используются, например, критерий «трех сигм», критерий Романовского, критерий Шарлея, вариационный критерий Диксона и другие.
Критерий «трех сигм» применяется для результатов измерений, распределенных по нормальному закону. По этому критерию считается, что результат, возникающий с вероятностью q 3S ,
где 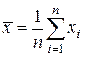
n – количество наблюдений или измерений.
Данный критерий надежен при числе измерений n > 20. 50.
Критерий Романовского применяется, если число измерений n 20). Тогда по теореме Бернулли число результатов, превышающих по абсолютному значению среднее арифметическое значение на величину КШS, будет n[l — Ф(КШ)], где Ф(КШ) — значение нормированной функции Лапласа для X = КШ. Если сомнительным в ряду результатов наблюдений является один результат, то n[1-Ф(КШ)] = 1. Отсюда Ф(КШ) = (n -1)/n.
Значения критерия Шарлье приведены в таблице1.2.
Таблица 1.2 – Значения критерия Шарлье
| n | |||||||
| КШ | 1,3 | 1,65 | 1,96 | 2,13 | 2,24 | 2,32 | 2,58 |
Пользуясь критерием Шарлье, отбрасывают результат, для значения которого в ряду из n наблюдений выполняется неравенство |хi — х̅| > КШS.
Вариационный критерий Диксона удобный и достаточно мощный (с малыми вероятностями ошибок). При его применении полученные результаты наблюдений записывают в вариационный возрастающий ряд х1, х2, . . ., xn (x1 Zq) = q. Значения Zq приведены в таблице 1.3
Таблица 1.3 – Значения критерия Диксона
| n | Zq при q, равном | ||
| 0,10 | 0,05 | 0,02 | 0,01 |
| 0,68 | 0,76 | 0,85 | 0,89 |
| 0,48 | 0,56 | 0,64 | 0,70 |
| 0,40 | 0,47 | 0,54 | 0,59 |
| 0,35 | 0,41 | 0,48 | 0,53 |
| 0,29 | 0,35 | 0,41 | 0,45 |
| 0,28 | 0,33 | 0,39 | 0,43 |
| 0,26 | 0,31 | 0,37 | 0,41 |
| 0,26 | 0,30 | 0,36 | 0,39 |
| 0,22 | 0,26 | 0,31 | 0,34 |
Кроме рассмотренных критериев, существуют и другие, например критерии Граббса и Шовенэ.
Источник
Глава 7. Грубые погрешности и методы их исключения
7.1. Понятие о грубых погрешностях
Грубая погрешность, или промах, — это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором. К ним можно отнести:
• неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
• неправильная запись результата наблюдений, значений отдельных мер использованного набора, например гирь;
• хаотические изменения параметров питающего СИ напряжения, например его амплитуды или частоты.
Грубые погрешности, как правило, возникают при однократных измерениях и обычно устраняются путем повторных измерений. Их причинами могут быть внезапные и кратковременные изменения условий измерения или оставшиеся незамеченными неисправности в аппаратуре.
7.2. Критерии исключения грубых погрешностей
При однократных измерениях обнаружить промах не представляется возможным. Для уменьшения вероятности появления промахов измерения проводят два-три раза и за результат принимают среднее арифметическое полученных отсчетов. При многократных измерениях для обнаружения промахов используют статистические критерии, предварительно определив, какому виду распределения соответствует результат измерений.
Вопрос о том, содержит ли результат наблюдений грубую погрешность, решается общими методами проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что результат наблюдения х, не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают как содержащий грубую погрешность и его исключают.
Для выявления грубых погрешностей задаются вероятностью q (уровнем значимости) того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений.
Критерий «трех сигм» применяется для результатов измерений, распределенных по нормальному закону. По этому критерию считается, что результат, возникающий с вероятностью q 3Sx , где Sx — оценка СКО измерений. Величины х и Sx вычисляют без учета экстремальных значений xi. Данный критерий надежен при числе измерений n > 20. 50.
Критерий Романовского применяется, если число измерений n 1,73 .
Критерий Романовского свидетельствует о необходимости отбрасывания последнего результата измерения.
Критерий Шарлье используется, если число наблюдений в ряду велико (n> 20). Тогда по теореме Бернулли [56] число результатов, превышающих по абсолютному значению среднее арифметическое значение на величину КШSx, будет n[l — Ф(КШ)], где Ф(КШ) — значение нормированной функции Лапласа для X = КШ. Если сомнительным в ряду результатов наблюдений является один результат, то n[1-Ф(Кш)] = 1. Отсюда Ф(КШ) = (n -1)/n.
Значения критерия Шарлье приведены в табл. 7.2.
Источник
ГРУБЫЕ ПОГРЕШНОСТИ И МЕТОДЫ ИХ ИСКЛЮЧЕНИЯ.
Практическое занятие №1
ГРУБЫЕ ПОГРЕШНОСТИ И МЕТОДЫ ИХ ИСКЛЮЧЕНИЯ.
Грубая погрешность, или промах, – это погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. При однократных измерениях обнаружить промах невозможно. При многократных измерениях для обнаружения промахов используют статистические критерии, такие как критерий Романовского, критерий Шарлье, критерий Диксона.
Критерий Романовского
Критерий Романовского применяется, если число измерений n 20). Пользуясь данным критерием, отбрасывается результат, для значения которого выполняется неравенство
Пример решения
При измерении расстояний между колоннами были получены следующие результаты (см. табл. 12).
Обработка результатов измерений
Находим СКО
Проверяем сомнительный результат измерения – 23,66. Для этого значения не выполняется неравенство 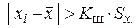
Значения критерия Шарлье
т. е.
Таким образом, проверяемое значение 23,66 не является промахом и не отбрасывается.
Критерий Диксона
При использовании данного критерия полученные результаты измерений записываются в вариационный возрастающий ряд x1 2 23,267 23,272 23,272 23,277 23,282
№ п.п. Результаты измерений 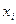
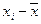
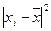
25,15 25,14 25,17 25,16 25,15 25,12 25,16 25,17 25,14 25,15 25,19 25,16 25,14 25,15 25,17 25,14 25,22 25,16 25,15 25,17 25,15 25,16 25,15 25,14 25,17 25,29 25,16 25,15 25,14 25,17
Практическое занятие №2
Пример.
Определить систематические погрешности и записать результат с учетом различных параметров.
Получен результат измерения длины стальной фермы xi = 24003 мм. Измерение выполнялось 3-метровой рулеткой из нержавеющей стали при t = -20 °С. При этом a1 = 20,5·10 -6 , a2 = 12,5·10 -6 , t1 = t2 = -20°С, 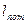
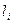
Решение
1. Поправка на температуру окружающей среды
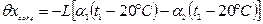

Действительную длину xi фермы с учетом поправки на температуру окружающей среды принимаем равной
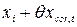
2. Поправка на относительную скорость внешней среды
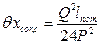

Действительную длину xi фермы с учетом поправки на относительную скорость внешней среды принимаем равной
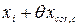
3. Поправка на длину шкалы средства измерения
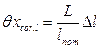
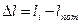
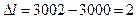
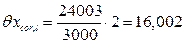
Действительную длину xi фермы с учетом поправки на длину шкалы средства измерения принимаем равной
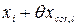
4. Поправка на несовпадение направлений линии измерения и измеряемого размера
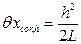
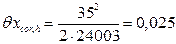
Действительную длину xi фермы с учетом поправки несовпадение направлений линии измерения и измеряемого размера принимаем равной
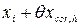
Действительную длину xi фермы с учетом всех поправок принимаем равной
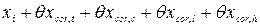
Задание
Определить систематические погрешности и записать результат с учетом различных параметров.
Данные результатов измерений приведены в таблице №16
Задача 3
А) ПРЕДВАРИТЕЛЬНАЯ ОЦЕНКА ВИДА РАСПРЕДЕЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЯ
Для предварительной оценки вида распределения по полученным данным строят гистограмму распределений или полигон распределения. В начале производится группирование – разделение данных от наименьшего xmin до наибольшего xmax на r интервалов. Для количества измерений от 30 до 100 рекомендуемое число интервалов – от 7 до 9. Ширину интервала выбирают постоянной для всего ряда данных, при этом следует иметь в виду, что ширина интервала должна быть больше погрешности округления при записи данных. Ширину интервала вычисляют по формуле
Вычисленное значение h обычно округляют. Например при h = 0,0187 это значение округляют до h = 0,02. Установив границы интервалов, подсчитывают число результатов измерений, попавших в каждый интервал. При построении гистограммы или полигона распределения масштаб этих графиков рекомендуется выбирать так, чтобы высота графика относилась к его основанию примерно как 3 к 5.
Пример
Построить гистограмму и полигон распределения по полученным экспериментальным данным, приведенным в табл. 17.
Результаты измерений
Определяем ширину интервала
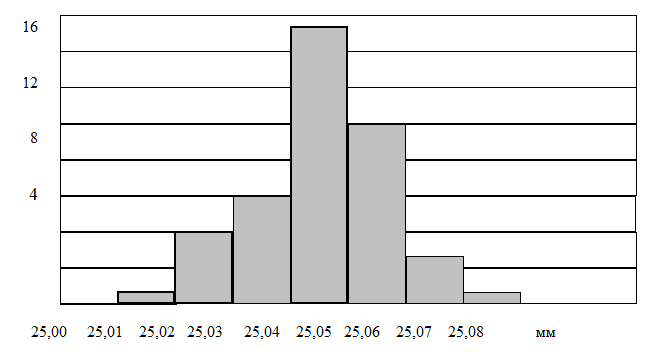
Строим гистограмму распределений (рис. 1), подсчитав число экспериментальных данных, попавших в каждый интервал.
Рис.1. Гистограмма распределений результатов измерений
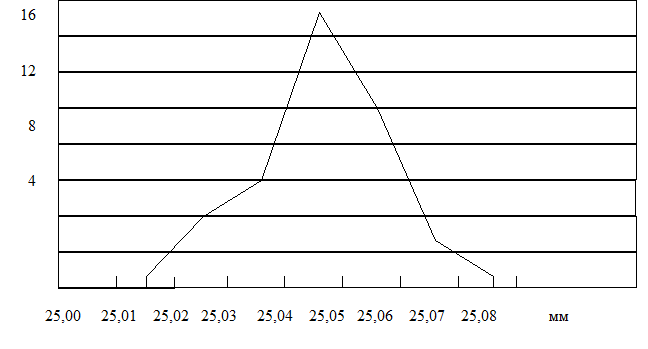
Далее, строим полигон распределения (рис. 2), который представляет собой кусочно-линейную аппроксимацию искомой функции плотности распределения результатов измерения.
Рис. 2. Полигон распределения результатов измерения
Б) ПРОВЕРКА ГИПОТЕЗЫ О НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Нормальный закон распределения, называемый часто распределением Гаусса описывается зависимостью
где σ – параметр рассеивания распределения, равный среднему квадратическому отклонению.
Широкое использование нормального распределения на практике объясняется теоремой теории вероятностей, утверждающей, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.
При количестве измерений n * – смещенное СКО;
Гипотеза о нормальности подтверждается, если
где 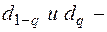
Значения процентных точек q для распределения d
Критерий 2. Гипотеза о нормальности распределения результатов измерения подтверждается, если не более m разностей 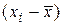
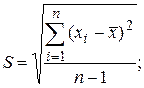
Значения доверительной вероятности P выбирают из табл. 19.
Значения доверительной вероятности Р
Пример
В табл. 19 приведены результаты измерения угла одним оператором, одним и тем же теодолитом, в одних и тех же условиях. Проверить, можно ли считать, что приведенные в табл. 20 данные принадлежат совокупности, распределенной нормально.
Результаты исследований
Оценка измеряемой величины равна
Средние квадратические отклонения S и S * найдем по формулам:
Оценка параметра d составит
Уровень значимости критерия 1 примем q = 2%. Из табл. 18 находим d1% = = 0,92 и d99% = 0,68. При определении d1% и d99% использовалась линейная интерполяция ввиду того, что значение n = 14 в таблице отсутствует. Критерий 1 выполняется, так как 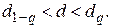
r = (10,00 ± 0,05) 10 2 м — радиус верхнего диска подвеса;
l = (233,0 ± 0,2) 10 2 м — длина нитей подвеса;
m = (125,7 ±0,1) 10 3 кг — масса платформы;
T= (2,81 ± 0,01) с — период малых колебаний платформы;
g = 9,81 м с г — ускорение свободного падения;
Результаты приведены со средними квадратичными отклонениями.
Решение.
Подставляя в исходную формулу средние арифметические значения измеряемых прямыми способами величин и округленные значения постоянных, получим оценку истинного значения моментов инерции платформы.
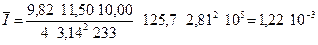
так как результат должен быть округлен до трех значащих цифр.
Для оценки точности полученного результата вычислим частные производные и частные погрешности косвенных измерений:
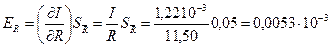
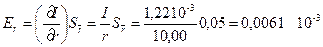
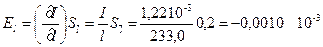
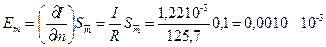
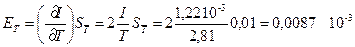
Таким образом, среднее квадратичное отклонение косвенного измерения момента инерции платформы составит
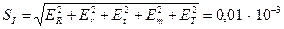
Окончательно результат косвенного измерения записывается в виде I=(1,22 ±·0,01) 10 3 кг м 2 .
Задание
Определить предельное усилие при растяжении полос при сварке в стык по длинной полосе, по данным приведенным в таблице № 26
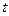
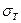
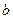
Продолжение таблица № 26
Практическое занятие №6
Пример
Определить в каком интервале находится измеренное значение, если при выполнении измерения прибором, имеющим на щитке обозначение 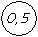
Решение
Определяем абсолютную погрешность измерения
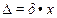
И измеряемое значение будет находиться в интервале 200±1
Задание
Практическое занятие №7
ВЫБОР СРЕДСТВ ИЗМЕРЕНИЙ.
Расчет погрешности при выборе методов и средств измерения выполняют в соответствии с требованиями ГОСТ 26433.0-85.
Методы и средства измерений принимаем в соответствии с характером объекта и измеряемых параметров из условия.
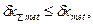
где 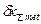
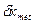
Вычисляем расчетную погрешность измерения по одной из формул:
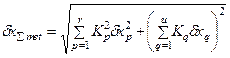
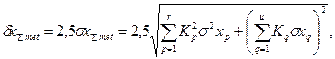
где 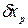
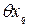
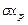
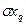
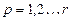
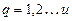
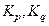
При расчете по указанным формулам принимаем, что составляющие погрешности независимы между собой или слабо коррелированны.
Предельную погрешность 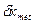
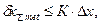
где 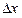
К — коэффициент, зависящий от цели измерений и характера объекта.
Для измерений, выполняемых в процессе и при контроле точности изготовления и установки элементов, а также при контроле точности разбивочных работ принимаем К = 0,2.
Для измерений, выполняемых в процессе производства разбивочных работ, К = 0,4.
Действительная погрешность 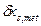
Для случаев, когда процесс измерения состоит из большого числа отдельных операций, на основе принципа равных влияний определяем среднее значение составляющих погрешностей 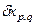
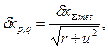
где 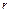
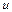
Выделяем те составляющие погрешности, которые легко могут быть уменьшены, увеличивая соответственно значения тех составляющих погрешностей, которые трудно обеспечить имеющимися методами и средствами.
Проверяем соблюдение условия (1) и в случае несоблюдения этого условия назначают более точные средства или принимают другой метод измерения.
Пример
Выбрать средство измерения для контроля длины изделия,
L = 3600 ± 2,0 мм ( 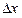
Решение
1. Определяем предельную погрешность измерения
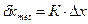
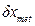
2. Для выполнения измерений применяем, например, 10-метровую металлическую рулетку 3-го класса точности ЗПК3-10АУТ/10 ГОСТ 7502-80.
3. В суммарную погрешность измерения длины изделия рулеткой входят составляющие погрешности: 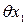
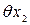
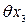
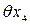
Определяем значения этих погрешностей.
3.1. Погрешность 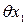
3.2. Погрешность 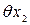
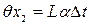
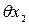
3.3. Погрешность 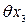
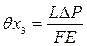
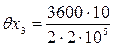
где 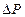
F = 2 мм 2 — площадь поперечного сечения рулетки;
E = 2·10 5 Н/мм — модуль упругости материала рулетки.
3.4. Экспериментально установлено, что погрешность снятия отсчета по шкале рулетки не превышает 0,3 мм, при этом погрешность 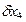
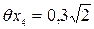
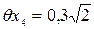
4. Определяем расчетную суммарную погрешность измерения по формуле (2), учитывая, что 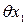
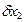
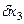
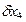
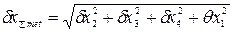
5. Данные метод и средство измерения могут быть приняты для выполнения измерений, так как расчетная суммарная погрешность измерения 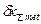
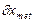
Задание
По выше описанному алгоритму произвести выбор средства измерения с учетом погрешности, используя данные в таблице №6
Практическое занятие №8
Пример.
Произвести предварительную оценку точности измерений рулеткой длины изделий при контроле точности их изготовления.
Решение
Измерение длины каждого изделия в процессе контроля будут выполняться при числе наблюдений m = 2.
Выполняем многократные наблюдения длины одного изделия при числе наблюдений М = 10. Для уменьшения влияния систематической погрешности первые пять наблюдений выполняем в одном направлении каждый раз со сдвигом шкалы рулетки на 70 — 90 мм, а вторые пять наблюдений — в другом направлении с тем же сдвигом шкалы.
Результаты наблюдений и последовательность их обработки приведены в табл. 8 (приведены результаты 10 наблюдений, т.е. М = 10).
1. Определяем среднее арифметическое из результатов измерений:
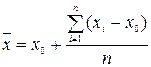
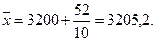
Принимаем 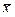
2. Контроль правильности вычислений:
а).
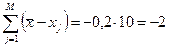
б). 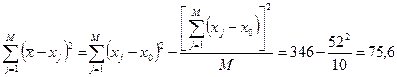
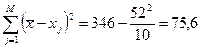
3. Среднее квадратическое отклонение результата измерений находим по формуле
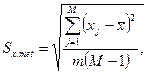
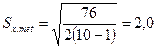
4. Действительная погрешность измерения будет составлять.
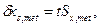

5. Предельную погрешность измерения находим по формуле
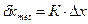
При допуске на длину 16.5 мм по 16 квалитету
6. Проверяем соблюдение условия
Действительная погрешность измерения не соответствует требуемой, должны быть приняты другие средства измерений или увеличено количество наблюдений т. Принимаем т = 5, тогда
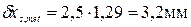
Источник